Chào mừng bạn đến với bài học về Lý thuyết Hình cầu trong chương trình Toán 9. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về hình cầu, bao gồm định nghĩa, các yếu tố của hình cầu, công thức tính diện tích và thể tích.
Chúng ta sẽ cùng nhau khám phá những tính chất đặc biệt của hình cầu và cách áp dụng chúng vào giải các bài toán thực tế. Hãy sẵn sàng để bước vào thế giới hình học không gian đầy thú vị!
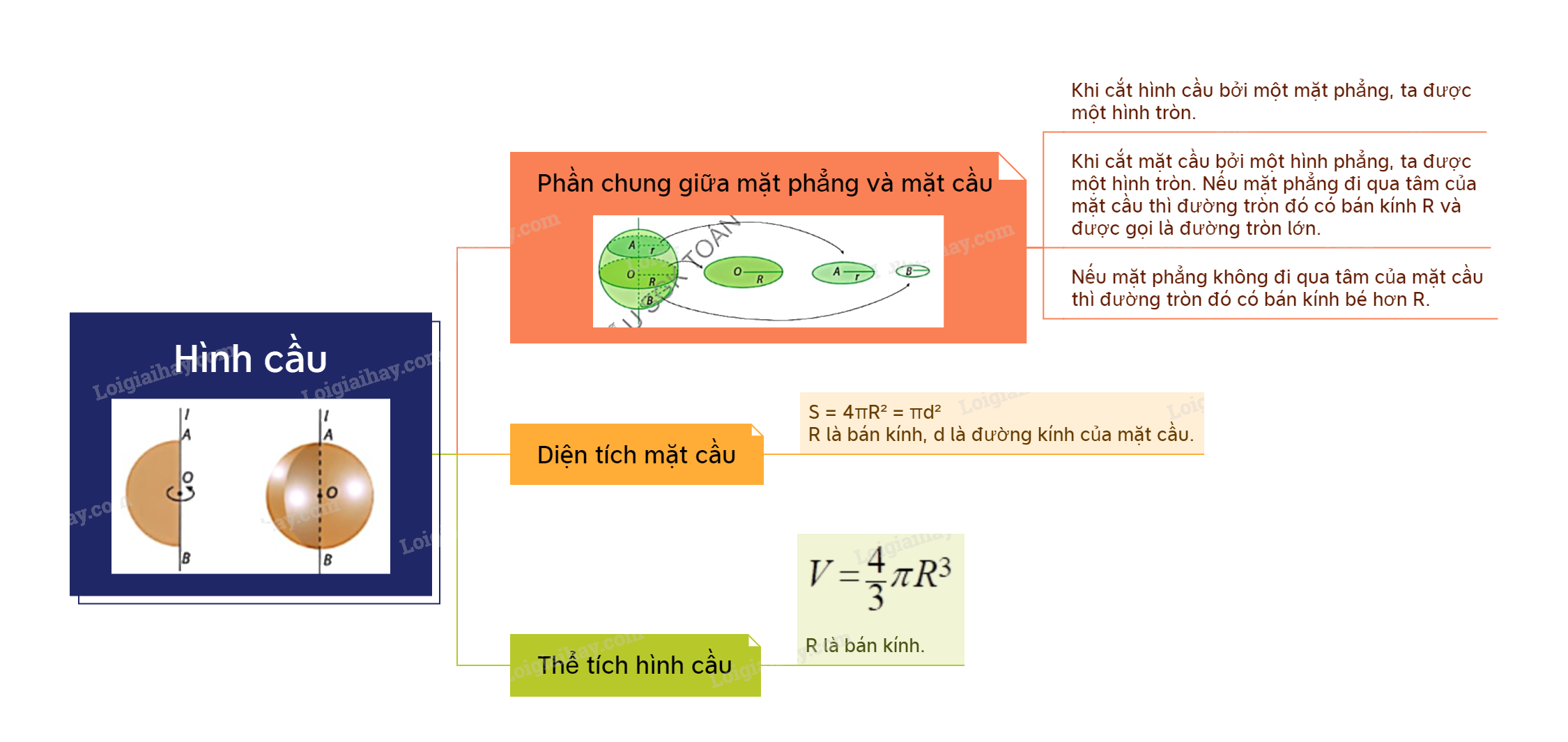
1. Hình cầu Khi cắt hình cầu bởi một mặt phẳng, ta được một hình tròn. Khi cắt mặt cầu bởi một hình phẳng, ta được một hình tròn. Nếu mặt phẳng đi qua tâm của mặt cầu thì đường tròn đó có bán kính R và được gọi là đường tròn lớn. Nếu mặt phẳng không đi qua tâm của mặt cầu thì đường tròn đó có bán kính bé hơn R.
1. Hình cầu
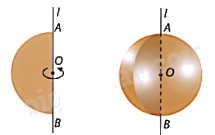
Khi cắt hình cầu bởi một mặt phẳng, ta được một hình tròn. Khi cắt mặt cầu bởi một hình phẳng, ta được một hình tròn. Nếu mặt phẳng đi qua tâm của mặt cầu thì đường tròn đó có bán kính R và được gọi là đường tròn lớn. Nếu mặt phẳng không đi qua tâm của mặt cầu thì đường tròn đó có bán kính bé hơn R. |
Ví dụ: Khi cắt hình cầu bởi các mặt phẳng khác nhau, ta được các hình tròn có bán kính khác nhau. 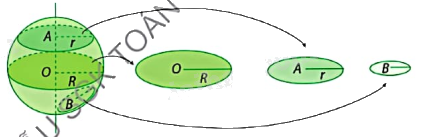
2. Diện tích của mặt cầu
Diện tích S của mặt cầu là: \(S = 4\pi {R^2} = \pi {d^2}\) Với R là bán kính và d là đường kính của mặt cầu. |
Ví dụ:
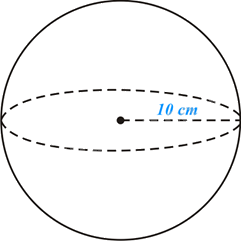
Diện tích mặt cầu là:
\(S = 4\pi {R^2} = 4\pi {.10^2} = 400\pi \left( {c{m^2}} \right)\),
3. Thể tích hình cầu
Thể tích của hình cầu có bán kính R là \(V = \frac{4}{3}\pi {R^3}\). |
Ví dụ:
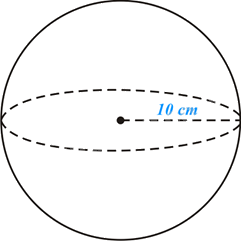
Thể tích hình cầu là:
\(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {.10^3} = \frac{{4000\pi }}{3}\left( {c{m^3}} \right)\).
Hình cầu là một hình học không gian quan trọng trong chương trình Toán 9. Để hiểu rõ về hình cầu, chúng ta cần nắm vững định nghĩa, các yếu tố cơ bản và các tính chất đặc trưng của nó.
Hình cầu là tập hợp tất cả các điểm trong không gian cách một điểm cố định (gọi là tâm) một khoảng không đổi (gọi là bán kính).
Việc nắm vững các công thức tính diện tích và thể tích hình cầu là rất quan trọng để giải các bài toán liên quan. Dưới đây là các công thức cần nhớ:
Diện tích mặt cầu (S) được tính theo công thức:
S = 4πR2
Trong đó:
Thể tích hình cầu (V) được tính theo công thức:
V = (4/3)πR3
Trong đó:
Bài toán 1: Tính diện tích mặt cầu có bán kính R = 5cm.
Giải:
S = 4πR2 = 4 * 3.14159 * 52 = 314.159 cm2
Bài toán 2: Tính thể tích hình cầu có bán kính R = 3cm.
Giải:
V = (4/3)πR3 = (4/3) * 3.14159 * 33 = 113.097 cm3
Hình cầu có mối liên hệ mật thiết với các hình học không gian khác như hình tròn, hình trụ và hình nón. Việc hiểu rõ mối liên hệ này sẽ giúp bạn giải quyết các bài toán phức tạp một cách dễ dàng hơn.
Ví dụ, khi cắt một hình cầu bằng một mặt phẳng, ta có thể thu được một hình tròn. Khi nội tiếp một hình cầu vào một hình trụ, ta có thể tính toán được mối quan hệ giữa bán kính của hình cầu và các kích thước của hình trụ.
Để nắm vững kiến thức về Lý thuyết Hình cầu Toán 9, bạn nên thực hành giải nhiều bài tập khác nhau. Hãy tìm kiếm các bài tập trong sách giáo khoa, sách bài tập hoặc trên các trang web học toán online như giaitoan.edu.vn.
Việc luyện tập thường xuyên sẽ giúp bạn hiểu sâu hơn về các khái niệm và công thức, đồng thời rèn luyện kỹ năng giải toán một cách hiệu quả.
Lý thuyết Hình cầu Toán 9 là một phần quan trọng trong chương trình học. Hy vọng rằng bài học này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về hình cầu. Hãy tiếp tục luyện tập và khám phá thêm nhiều điều thú vị trong thế giới hình học không gian!