Bài tập 5.20 trang 114 SGK Toán 9 tập 1 là một bài toán quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
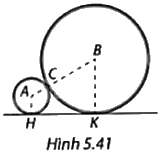
Hình 5.41 cho thấy mặt cắt của hai ống nước nhựa được đặt sát nhau trên mặt đất. Ống nhỏ có đường kính 6cm, ống lớn có đường kính 18cm. Tính: a) Khoảng cách AB giữa tâm của hai mặt cắt; b) Khoảng cách HK giữa hai tiếp điểm của mặt cắt hai ống với mặt đất.
Đề bài
Hình 5.41 cho thấy mặt cắt của hai ống nước nhựa được đặt sát nhau trên mặt đất. Ống nhỏ có đường kính 6cm, ống lớn có đường kính 18cm. Tính:
a) Khoảng cách AB giữa tâm của hai mặt cắt;
b) Khoảng cách HK giữa hai tiếp điểm của mặt cắt hai ống với mặt đất.
Phương pháp giải - Xem chi tiết
a) Cho hai đường tròn phân biệt (O; R) và (O’; r) và \(d = OO'\). Nếu \(d = R + r\) thì hai đường tròn tiếp xúc ngoài.
b) + Qua C kẻ đường thẳng vuông góc với AB, cắt HK tại E.
+ Suy ra CE là tiếp tuyến của đường tròn (A) và CE là tiếp tuyến của đường tròn (B).
+ Sử dụng tính chất hai tiếp tuyến cắt nhau suy ra:
\(CE = EH,\widehat {CEA} = \widehat {AEH} = \frac{1}{2}\widehat {HEC}\), \(CE = EK,\widehat {CEB} = \widehat {BEK} = \frac{1}{2}\widehat {KEC}\).
+ Chứng minh \(HK = EH + EK = 2CE\)
+ Chứng minh \(\widehat {AEB} = {90^o}\).
+ Chứng minh \(\Delta ACE\backsim \Delta ECB\left( g.g \right)\), \(E{C^2} = AC.CB\), tính được EC.
Lời giải chi tiết
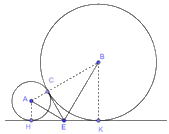
a) Bán kính đường tròn nhỏ là: \(AC = AH = \frac{6}{2} = 3cm\), bán kính đường tròn lớn là: \(BC = BK = \frac{{18}}{2} = 9cm\)
Vì hai đường tròn (A) và (B) tiếp xúc ngoài tại C nên \(AB = AC + CB = 3 + 9 = 12\left( {cm} \right)\)
b) Qua C kẻ đường thẳng vuông góc với AB, cắt HK tại E.
Do đó, CE là tiếp tuyến của đường tròn (A) và CE là tiếp tuyến của đường tròn (B).
Vì CE và HE là tiếp tuyến của đường tròn (A) nên \(CE = EH,\widehat {CEA} = \widehat {AEH} = \frac{1}{2}\widehat {HEC}\).
Vì CE và EK là tiếp tuyến của đường tròn (B) nên \(CE = EK,\widehat {CEB} = \widehat {BEK} = \frac{1}{2}\widehat {KEC}\).
Do đó, \(HK = EH + EK = 2CE\).
Ta có: \(\widehat {HEC} + \widehat {CEK} = {180^o}\), nên \(\frac{1}{2}\left( {\widehat {HEC} + \widehat {CEK}} \right) = {90^0}\), suy ra \(\widehat {AEC} + \widehat {CEB} = {90^o}\) hay \(\widehat {AEB} = {90^o}\).
Tam giác ACE và tam giác ECB có: \(\widehat {ECA} = \widehat {ECB} = {90^o},\widehat {CAE} = \widehat {CEB}\) (cùng phụ với góc AEC).
Do đó, \(\Delta ACE\backsim \Delta ECB\left( g.g \right)\), suy ra \(\frac{{CE}}{{CB}} = \frac{{AC}}{{EC}}\), suy ra \(E{C^2} = AC.CB = 3.9 = 27\), suy ra \(EC = 3\sqrt 3 cm\).
Vậy \(HK = 2CE = 6\sqrt 3 cm\).
Bài tập 5.20 trang 114 SGK Toán 9 tập 1 thuộc chương Hàm số bậc nhất và hàm số bậc hai. Bài toán này thường yêu cầu học sinh xác định hệ số góc, điểm đi qua của đường thẳng, hoặc tìm giao điểm của hai đường thẳng. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về hàm số, phương trình đường thẳng và hệ phương trình bậc nhất hai ẩn.
Trước khi bắt đầu giải bài tập, điều quan trọng là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Đôi khi, đề bài có thể yêu cầu tìm một giá trị cụ thể, hoặc chứng minh một đẳng thức nào đó. Việc hiểu rõ yêu cầu sẽ giúp học sinh lựa chọn phương pháp giải phù hợp và tránh sai sót không đáng có.
Có nhiều phương pháp khác nhau để giải bài tập 5.20 trang 114 SGK Toán 9 tập 1, tùy thuộc vào yêu cầu cụ thể của từng bài toán. Dưới đây là một số phương pháp phổ biến:
Giả sử bài tập 5.20 yêu cầu tìm giao điểm của hai đường thẳng y = 2x + 1 và y = -x + 4. Để giải bài tập này, chúng ta có thể sử dụng phương pháp thế. Ta có:
2x + 1 = -x + 4
3x = 3
x = 1
Thay x = 1 vào phương trình y = 2x + 1, ta được:
y = 2(1) + 1 = 3
Vậy giao điểm của hai đường thẳng là (1, 3).
Để nắm vững kiến thức và kỹ năng giải bài tập 5.20 trang 114 SGK Toán 9 tập 1, học sinh cần luyện tập thường xuyên với các bài tập tương tự. Ngoài ra, học sinh cũng nên tham khảo các tài liệu tham khảo khác, như sách bài tập, đề thi thử, và các trang web học toán online.
Ngoài bài tập tìm giao điểm của hai đường thẳng, bài tập 5.20 trang 114 SGK Toán 9 tập 1 còn có thể xuất hiện ở nhiều dạng khác nhau, như:
Để giải bài tập 5.20 trang 114 SGK Toán 9 tập 1 một cách hiệu quả, học sinh nên:
Bài tập 5.20 trang 114 SGK Toán 9 tập 1 là một bài toán quan trọng trong chương trình học. Việc nắm vững kiến thức và kỹ năng giải bài tập này sẽ giúp học sinh tự tin hơn trong các kỳ thi và đạt kết quả tốt hơn trong môn Toán.