Chào mừng các em học sinh đến với bài giải bài tập 5.5 trang 102 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương Hàm số bậc nhất và là một phần quan trọng trong việc củng cố kiến thức về hàm số.
Chúng tôi sẽ cung cấp lời giải chi tiết, dễ hiểu cùng với các phương pháp giải hiệu quả để giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
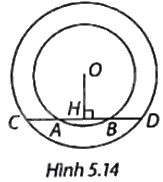
Trong Hình 5.14, cho hai đường tròn cùng tâm O, các điểm A, B, C, D thẳng hàng và \(OH \bot AB\left( {H \in AB} \right)\). a) Chứng minh rằng H là trung điểm của AB và CD. b) Chứng minh rằng \(AC = BD\). c) Biết bán kính đường tròn lớn là 10cm, \(CD = 16cm\) và \(AB = 8cm\). Tính bán kính đường tròn nhỏ.
Đề bài
Trong Hình 5.14, cho hai đường tròn cùng tâm O, các điểm A, B, C, D thẳng hàng và \(OH \bot AB\left( {H \in AB} \right)\).
a) Chứng minh rằng H là trung điểm của AB và CD.
b) Chứng minh rằng \(AC = BD\).
c) Biết bán kính đường tròn lớn là 10cm, \(CD = 16cm\) và \(AB = 8cm\). Tính bán kính đường tròn nhỏ.
Phương pháp giải - Xem chi tiết
a) Xét đường tròn (O, OC) có: \(OC = OD\) nên tam giác COD cân tại O. Do đó, OH là đường cao đồng thời là đường trung tuyến. Suy ra, H là trung điểm của CD.
Xét (O, OA) có: \(OA = OB\) nên tam giác OAB cân tại O. Do đó, OH là đường cao đồng thời là đường trung tuyến. Suy ra, H là trung điểm của AB.
b) Theo a ta có: \(CH = HD\), \(AH = HB\) nên \(CH - HA = HD - HB\), suy ra \(AC = BD\).
c) Tam giác HOD vuông tại H nên \(O{H^2} + H{D^2} = O{D^2}\)
Tam giác HOB vuông tại H nên \(O{B^2} = O{H^2} + H{B^2}\), từ đó tính được bán kính đường tròn nhỏ.
Lời giải chi tiết
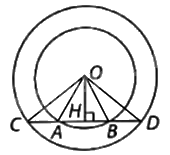
a) Xét đường tròn (O, OC) có: \(OC = OD\) nên tam giác COD cân tại O. Do đó, OH là đường cao đồng thời là đường trung tuyến. Suy ra, H là trung điểm của CD. Do đó, \(CH = HD\).
Xét (O, OA) có: \(OA = OB\) nên tam giác OAB cân tại O. Do đó, OH là đường cao đồng thời là đường trung tuyến. Suy ra, H là trung điểm của AB. Do đó, \(AH = HB\).
b) Theo a ta có: \(CH = HD\), \(AH = HB\) nên \(CH - HA = HD - HB\), suy ra \(AC = BD\).
c) Ta có:
\(\begin{array}{l}HD = \frac{1}{2}CD = \frac{1}{2}.16 = 8\left( {cm} \right),\\HB = \frac{1}{2}AB = \frac{1}{2}.8 = 4\left( {cm} \right)\end{array}\).
Tam giác HOD vuông tại H nên
\(O{H^2} + H{D^2} = O{D^2}\) (định lí Pythagore),
suy ra \(O{H^2}\) \( = O{D^2} - H{D^2}\) \( = {10^2} - {8^2}\) \( = 36\left( {cm} \right)\).
Tam giác HOB vuông tại H nên
\(O{B^2} = O{H^2} + H{B^2} = 36 + {4^2} = 52\) (định lí Pythagore),
suy ra \(OB = 2\sqrt {13} cm\).
Bài tập 5.5 trang 102 SGK Toán 9 tập 1 yêu cầu chúng ta xét hàm số y = (m-2)x + 3. Để hàm số này là hàm số bậc nhất, điều kiện cần và đủ là hệ số của x khác 0, tức là m - 2 ≠ 0. Việc hiểu rõ điều kiện này là nền tảng để giải quyết bài toán.
Đề bài yêu cầu chúng ta tìm giá trị của m để hàm số y = (m-2)x + 3 là hàm số bậc nhất. Để làm được điều này, chúng ta cần nắm vững định nghĩa của hàm số bậc nhất và áp dụng điều kiện m - 2 ≠ 0.
Để hàm số y = (m-2)x + 3 là hàm số bậc nhất, ta cần có:
m - 2 ≠ 0
Suy ra:
m ≠ 2
Vậy, với mọi giá trị của m khác 2, hàm số y = (m-2)x + 3 là hàm số bậc nhất.
Ví dụ 1: Nếu m = 3, hàm số trở thành y = (3-2)x + 3 = x + 3. Đây là hàm số bậc nhất vì hệ số của x là 1, khác 0.
Ví dụ 2: Nếu m = 2, hàm số trở thành y = (2-2)x + 3 = 0x + 3 = 3. Đây không phải là hàm số bậc nhất mà là hàm số hằng.
Các bài tập tương tự thường yêu cầu chúng ta xác định giá trị của tham số để hàm số thỏa mãn một điều kiện nào đó, chẳng hạn như hàm số đồng biến, nghịch biến, đi qua một điểm cho trước, hoặc có đồ thị thỏa mãn một tính chất nào đó. Để giải các bài tập này, chúng ta cần:
Khi giải bài tập về hàm số bậc nhất, các em cần lưu ý những điều sau:
Để củng cố kiến thức, các em hãy thử giải các bài tập sau:
Bài tập 5.5 trang 102 SGK Toán 9 tập 1 là một bài tập cơ bản về hàm số bậc nhất. Việc nắm vững kiến thức và phương pháp giải bài tập này sẽ giúp các em tự tin hơn khi giải các bài tập phức tạp hơn về hàm số.
| Khái niệm | Định nghĩa |
|---|---|
| Hàm số bậc nhất | Hàm số có dạng y = ax + b, trong đó a và b là các số thực và a ≠ 0. |
| Hệ số góc | Hệ số a trong hàm số y = ax + b. |
| Hệ số tự do | Hệ số b trong hàm số y = ax + b. |
Hy vọng với lời giải chi tiết và các kiến thức bổ trợ trên, các em sẽ hiểu rõ hơn về bài tập 5.5 trang 102 SGK Toán 9 tập 1 và có thể tự tin giải các bài tập tương tự. Chúc các em học tốt!