Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 1 trang 8 và 9 của sách giáo khoa Toán 9 tập 1. Mục tiêu của chúng ta là nắm vững kiến thức và kỹ năng giải toán, từ đó đạt kết quả tốt nhất trong học tập.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em tự học tại nhà hiệu quả. Các em có thể tham khảo các bước giải, cách làm và đối chiếu với bài làm của mình để hiểu rõ hơn về bài toán.
a) Số tuổi của anh là \(x\), số tuổi của em là \(y\). Lập một hệ thức biểu diễn sự liên hệ giữa \(x\) và \(y\), biết anh lớn hơn em 5 tuổi. b) 500 kg gạo được chia thành \(x\) bao 50 kg và \(y\) bao 20 kg. Lập một hệ thức biểu diễn sự liên hệ giữa \(x\) và \(y\).
Trả lời câu hỏi Luyện tập 1 trang 8SGK Toán 9 Cùng khám phá
Chỉ ra các phương trình bậc nhất hai ẩn \(x\) và \(y\) trong các phương trình sau:
\(\begin{array}{l}5y - x = - 2;\\3{x^2} - 10y = 1;\\\frac{{{x^2}}}{{x + 1}} - y = 0;\\x + 0y = 4;\\{y^2} - 9x = - 6.\end{array}\)
Phương pháp giải:
Dựa vào định nghĩa phương trình bậc nhất hai ẩn \(x\) và \(y\) để xác định.
Lời giải chi tiết:
Các phương trình bậc nhất hai ẩn \(x\) và \(y\) là: \(5y - x = - 2;\,\,x + 0y = 4\).
Trả lời câu hỏi Hoạt động 1 trang 8 SGK Toán 9 Cùng khám phá
a) Số tuổi của anh là \(x\), số tuổi của em là \(y\). Lập một hệ thức biểu diễn sự liên hệ giữa \(x\) và \(y\), biết anh lớn hơn em 5 tuổi.
b) 500 kg gạo được chia thành \(x\) bao 50 kg và \(y\) bao 20 kg. Lập một hệ thức biểu diễn sự liên hệ giữa \(x\) và \(y\).
Phương pháp giải:
Dựa vào các mối liên hệ giữa \(x\) và \(y\) để lập hệ thức.
Lời giải chi tiết:
a) Do anh lớn hơn em 5 tuổi nên ta có hệ thức biểu diễn sự liên hệ giữa \(x\) và \(y\) là: \(x - y = 5\).
b) Do 500 kg gạo được chia thành \(x\) bao 50 kg và \(y\) bao 20 kg nên ta có hệ thức biểu diễn sự liên hệ giữa \(x\) và \(y\) là: \(50x + 20y = 500\).
Trả lời câu hỏi Hoạt động 2 trang 9SGK Toán 9 Cùng khám phá
a) Cặp số \(\left( {x_1^{};y_1^{}} \right) = \left( {8;5} \right)\) có thỏa mãn \(50x_1^{} + 20y_1^{} = 500\) không?
b) Tìm một cặp số \(\left( {x_2^{};y_2^{}} \right)\) khác cặp số \(\left( {8;5} \right)\) sao cho \(50x_2^{} + 20y_2^{} = 500\).
c) Tìm một cặp số \(\left( {x_3^{};y_3^{}} \right)\) sao cho \(50x_3^{} + 20y_3^{} \ne 500\).
Phương pháp giải:
a) Thay cặp số vào phương trình để kiểm tra.
b) Thay \(x\) vào phương trình để tìm \(y\) rồi xác định cặp số.
c) Cho một cặp số khác 2 cặp số vừa tìm được.
Lời giải chi tiết:
a) Vì \(50.8 + 20.5 = 500\) nên cặp số \(\left( {8;5} \right)\) thỏa mãn \(50x_1^{} + 20y_1^{} = 500\).
b) Thay \(y_2^{} = 10\) vào phương trình ta được:
\(\begin{array}{l}50x_2^{} + 20.10 = 500\\50x_2^{} = 300\\x_2^{} = 6\end{array}\)
Vậy cặp số \(\left( {6;10} \right)\) là một cặp số thỏa mãn \(50x_2^{} + 20y_2^{} = 500\).
c) Vì \(50.8 + 20.3 \ne 500\) nên cặp số \(\left( {8;3} \right)\) thỏa mãn \(50x_3^{} + 20y_3^{} \ne 500\).
Trả lời câu hỏi Luyện tập 2 trang 9 SGK Toán 9 Cùng khám phá
Tìm bốn nghiệm của phương trình \(3x - 4y = 5\).
Phương pháp giải:
Tìm cặp số thỏa mãn phương trình để kết luận nghiệm.
Lời giải chi tiết:
+ Vì \(3.1 - 4.\frac{{ - 1}}{2} = 5\) nên cặp số \(\left( {1; - \frac{1}{2}} \right)\) là một nghiệm của phương trình \(3x - 4y = 5\).
+ Vì \(3.2 - 4.\frac{1}{4} = 5\) nên cặp số \(\left( {2;\frac{1}{4}} \right)\) là một nghiệm của phương trình \(3x - 4y = 5\).
+ Vì \(3.3 - 4.1 = 5\) nên cặp số \(\left( {3;1} \right)\) là một nghiệm của phương trình \(3x - 4y = 5\).
+ Vì \(3.4 - 4.\frac{7}{4} = 5\) nên cặp số \(\left( {4;\frac{7}{4}} \right)\) là một nghiệm của phương trình \(3x - 4y = 5\).
Trả lời câu hỏi Hoạt động 1 trang 8 SGK Toán 9 Cùng khám phá
a) Số tuổi của anh là \(x\), số tuổi của em là \(y\). Lập một hệ thức biểu diễn sự liên hệ giữa \(x\) và \(y\), biết anh lớn hơn em 5 tuổi.
b) 500 kg gạo được chia thành \(x\) bao 50 kg và \(y\) bao 20 kg. Lập một hệ thức biểu diễn sự liên hệ giữa \(x\) và \(y\).
Phương pháp giải:
Dựa vào các mối liên hệ giữa \(x\) và \(y\) để lập hệ thức.
Lời giải chi tiết:
a) Do anh lớn hơn em 5 tuổi nên ta có hệ thức biểu diễn sự liên hệ giữa \(x\) và \(y\) là: \(x - y = 5\).
b) Do 500 kg gạo được chia thành \(x\) bao 50 kg và \(y\) bao 20 kg nên ta có hệ thức biểu diễn sự liên hệ giữa \(x\) và \(y\) là: \(50x + 20y = 500\).
Trả lời câu hỏi Luyện tập 1 trang 8SGK Toán 9 Cùng khám phá
Chỉ ra các phương trình bậc nhất hai ẩn \(x\) và \(y\) trong các phương trình sau:
\(\begin{array}{l}5y - x = - 2;\\3{x^2} - 10y = 1;\\\frac{{{x^2}}}{{x + 1}} - y = 0;\\x + 0y = 4;\\{y^2} - 9x = - 6.\end{array}\)
Phương pháp giải:
Dựa vào định nghĩa phương trình bậc nhất hai ẩn \(x\) và \(y\) để xác định.
Lời giải chi tiết:
Các phương trình bậc nhất hai ẩn \(x\) và \(y\) là: \(5y - x = - 2;\,\,x + 0y = 4\).
Trả lời câu hỏi Hoạt động 2 trang 9SGK Toán 9 Cùng khám phá
a) Cặp số \(\left( {x_1^{};y_1^{}} \right) = \left( {8;5} \right)\) có thỏa mãn \(50x_1^{} + 20y_1^{} = 500\) không?
b) Tìm một cặp số \(\left( {x_2^{};y_2^{}} \right)\) khác cặp số \(\left( {8;5} \right)\) sao cho \(50x_2^{} + 20y_2^{} = 500\).
c) Tìm một cặp số \(\left( {x_3^{};y_3^{}} \right)\) sao cho \(50x_3^{} + 20y_3^{} \ne 500\).
Phương pháp giải:
a) Thay cặp số vào phương trình để kiểm tra.
b) Thay \(x\) vào phương trình để tìm \(y\) rồi xác định cặp số.
c) Cho một cặp số khác 2 cặp số vừa tìm được.
Lời giải chi tiết:
a) Vì \(50.8 + 20.5 = 500\) nên cặp số \(\left( {8;5} \right)\) thỏa mãn \(50x_1^{} + 20y_1^{} = 500\).
b) Thay \(y_2^{} = 10\) vào phương trình ta được:
\(\begin{array}{l}50x_2^{} + 20.10 = 500\\50x_2^{} = 300\\x_2^{} = 6\end{array}\)
Vậy cặp số \(\left( {6;10} \right)\) là một cặp số thỏa mãn \(50x_2^{} + 20y_2^{} = 500\).
c) Vì \(50.8 + 20.3 \ne 500\) nên cặp số \(\left( {8;3} \right)\) thỏa mãn \(50x_3^{} + 20y_3^{} \ne 500\).
Trả lời câu hỏi Luyện tập 2 trang 9 SGK Toán 9 Cùng khám phá
Tìm bốn nghiệm của phương trình \(3x - 4y = 5\).
Phương pháp giải:
Tìm cặp số thỏa mãn phương trình để kết luận nghiệm.
Lời giải chi tiết:
+ Vì \(3.1 - 4.\frac{{ - 1}}{2} = 5\) nên cặp số \(\left( {1; - \frac{1}{2}} \right)\) là một nghiệm của phương trình \(3x - 4y = 5\).
+ Vì \(3.2 - 4.\frac{1}{4} = 5\) nên cặp số \(\left( {2;\frac{1}{4}} \right)\) là một nghiệm của phương trình \(3x - 4y = 5\).
+ Vì \(3.3 - 4.1 = 5\) nên cặp số \(\left( {3;1} \right)\) là một nghiệm của phương trình \(3x - 4y = 5\).
+ Vì \(3.4 - 4.\frac{7}{4} = 5\) nên cặp số \(\left( {4;\frac{7}{4}} \right)\) là một nghiệm của phương trình \(3x - 4y = 5\).
Trả lời câu hỏi Luyện tập 3 trang 9 SGK Toán 9 Cùng khám phá
Trong mặt phẳng tọa độ \(Oxy\), hãy biểu diễn các nghiệm của mỗi phương trình sau:
a) \(4x - y = 3\)
b) \(0x - 2y = 5\)
c) \(7x + 0y = 21\)
Phương pháp giải:
+ Biểu diễn \(x\) theo \(y\) hoặc \(y\) theo \(x\).
+ Tìm hai cặp số là nghiệm của phương trình.
+ Vẽ đồ thị.
Lời giải chi tiết:
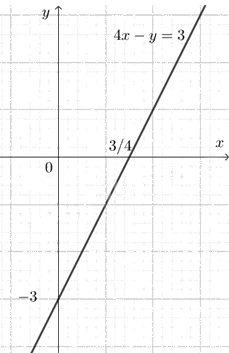
a) Xét phương trình \(4x - y = 3\). (1)
Chuyển vế, ta có \(y = 4x - 3\).
Nếu cho \(x\) một giá trị bất kì thì cặp số \(\left( {x;y} \right)\), trong đó \(y = 4x - 3\), là một nghiệm của phương trình (1) có các nghiệm là \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = 4x - 3.\end{array} \right.\)
Trong mặt phẳng tọa độ \(Oxy\), tập hợp các điểm biểu diễn các nghiệm của phương trình (1) là đường thẳng \(y = 4x - 3\).
b) Xét phương trình \(0x - 2y = 5\). (2)
Từ (2), ta có \(2y = 5\) hay \(y = \frac{5}{2}\).
Nếu cho \(x\) một giá trị bất kì thì cặp số \(\left( {x;y} \right)\), trong đó \(y = \frac{5}{2}\), là một nghiệm của phương trình (2).
Do đó phương trình (2) có các nghiệm là \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = \frac{5}{2}.\end{array} \right.\)
Trong mặt phẳng tọa độ \(Oxy\), tập hợp các điểm biểu diễn các nghiệm của phương trình (2) là đường thẳng đi qua điểm \(A\left( {0;\frac{5}{2}} \right)\) và song song với trục hoành (ta gọi đường thẳng này là đường thẳng \(y = \frac{5}{2}\)).

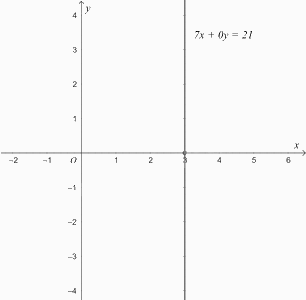
c) Xét phương trình \(7x + 0y = 21\). (3)
Từ (3), ta có \(7x = 21\) hay \(x = 3\).
Nếu cho \(y\) một giá trị bất kì thì cặp số \(\left( {x;y} \right)\), tron đó \(x = 3\), là một nghiệm của phương trình (3).
Do đó phương trình (3) có các nghiệm là: \(\left\{ \begin{array}{l}x = 3\\y \in \mathbb{R}.\end{array} \right.\)
Trong mặt phẳng tọa độ \(Oxy\), tập hợp các điểm biểu diễn các nghiệm của phương trình (3) là đường thẳng đi qua điểm \(B\left( { - 3;0} \right)\) và song song với trục tung (ta gọi đường thẳng này là đường thẳng \(x = 3\)).
Trả lời câu hỏi Luyện tập 3 trang 9 SGK Toán 9 Cùng khám phá
Trong mặt phẳng tọa độ \(Oxy\), hãy biểu diễn các nghiệm của mỗi phương trình sau:
a) \(4x - y = 3\)
b) \(0x - 2y = 5\)
c) \(7x + 0y = 21\)
Phương pháp giải:
+ Biểu diễn \(x\) theo \(y\) hoặc \(y\) theo \(x\).
+ Tìm hai cặp số là nghiệm của phương trình.
+ Vẽ đồ thị.
Lời giải chi tiết:
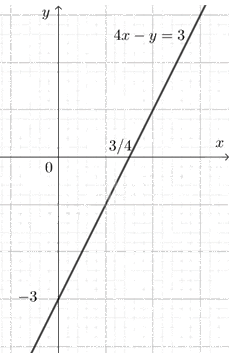
a) Xét phương trình \(4x - y = 3\). (1)
Chuyển vế, ta có \(y = 4x - 3\).
Nếu cho \(x\) một giá trị bất kì thì cặp số \(\left( {x;y} \right)\), trong đó \(y = 4x - 3\), là một nghiệm của phương trình (1) có các nghiệm là \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = 4x - 3.\end{array} \right.\)
Trong mặt phẳng tọa độ \(Oxy\), tập hợp các điểm biểu diễn các nghiệm của phương trình (1) là đường thẳng \(y = 4x - 3\).
b) Xét phương trình \(0x - 2y = 5\). (2)
Từ (2), ta có \(2y = 5\) hay \(y = \frac{5}{2}\).
Nếu cho \(x\) một giá trị bất kì thì cặp số \(\left( {x;y} \right)\), trong đó \(y = \frac{5}{2}\), là một nghiệm của phương trình (2).
Do đó phương trình (2) có các nghiệm là \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = \frac{5}{2}.\end{array} \right.\)
Trong mặt phẳng tọa độ \(Oxy\), tập hợp các điểm biểu diễn các nghiệm của phương trình (2) là đường thẳng đi qua điểm \(A\left( {0;\frac{5}{2}} \right)\) và song song với trục hoành (ta gọi đường thẳng này là đường thẳng \(y = \frac{5}{2}\)).

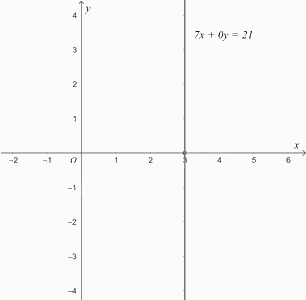
c) Xét phương trình \(7x + 0y = 21\). (3)
Từ (3), ta có \(7x = 21\) hay \(x = 3\).
Nếu cho \(y\) một giá trị bất kì thì cặp số \(\left( {x;y} \right)\), tron đó \(x = 3\), là một nghiệm của phương trình (3).
Do đó phương trình (3) có các nghiệm là: \(\left\{ \begin{array}{l}x = 3\\y \in \mathbb{R}.\end{array} \right.\)
Trong mặt phẳng tọa độ \(Oxy\), tập hợp các điểm biểu diễn các nghiệm của phương trình (3) là đường thẳng đi qua điểm \(B\left( { - 3;0} \right)\) và song song với trục tung (ta gọi đường thẳng này là đường thẳng \(x = 3\)).
Mục 1 của chương trình Toán 9 tập 1 thường tập trung vào việc ôn tập và hệ thống hóa kiến thức về các phép toán cơ bản, các biểu thức đại số và các phương trình bậc nhất một ẩn. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Bài 1 thường yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia số hữu tỉ, số vô tỉ, phân số, và các biểu thức đại số đơn giản. Để giải bài tập này, học sinh cần nắm vững các quy tắc về thứ tự thực hiện các phép toán, các tính chất giao hoán, kết hợp, phân phối của các phép toán.
Bài 2 thường yêu cầu học sinh giải các phương trình bậc nhất một ẩn có dạng ax + b = 0. Để giải bài tập này, học sinh cần nắm vững các bước giải phương trình, các phép biến đổi tương đương phương trình.
Bài 3 thường yêu cầu học sinh vận dụng kiến thức về phương trình bậc nhất một ẩn để giải các bài toán thực tế. Để giải bài tập này, học sinh cần đọc kỹ đề bài, xác định các đại lượng cần tìm, lập phương trình và giải phương trình.
Ví dụ 3: Một người đi xe máy từ A đến B với vận tốc 40km/h. Sau 1 giờ 30 phút, người đó còn cách B 20km. Tính quãng đường AB.
Lời giải:
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau:
Việc giải bài tập mục 1 trang 8, 9 SGK Toán 9 tập 1 là bước khởi đầu quan trọng trong quá trình học tập môn Toán 9. Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh sẽ tự tin hơn trong việc giải bài tập và đạt kết quả tốt nhất.