Chào mừng các em học sinh đến với bài giải bài tập 2.2 trang 36 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương Hàm số bậc nhất, một trong những kiến thức quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chép lại bảng bên và điền vào những ô có dấu “?” trong bảng đó để ô bên trái và bên phải của bảng biểu diễn cùng một thông tin.
Đề bài
Chép lại bảng bên và điền vào những ô có dấu “?” trong bảng đó để ô bên trái và bên phải của bảng biểu diễn cùng một thông tin.
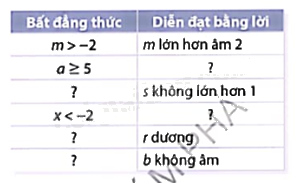
Phương pháp giải - Xem chi tiết
Dựa vào định nghĩa bất đẳng thức để giải bài toán.
Lời giải chi tiết
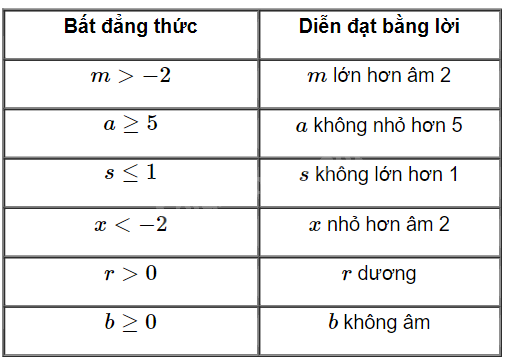
Bài tập 2.2 trang 36 SGK Toán 9 tập 1 yêu cầu chúng ta xác định các hàm số bậc nhất và tìm hệ số a của chúng. Để giải bài tập này, chúng ta cần nắm vững định nghĩa về hàm số bậc nhất: y = ax + b, trong đó a và b là các số thực, và a khác 0.
1. Lý thuyết cần nắm vững:
2. Phân tích bài tập 2.2:
Bài tập 2.2 thường đưa ra các biểu thức và yêu cầu xác định xem biểu thức nào là hàm số bậc nhất. Để làm được điều này, chúng ta cần biến đổi biểu thức về dạng y = ax + b và kiểm tra xem a có khác 0 hay không.
3. Giải chi tiết bài tập 2.2:
(Giả sử bài tập 2.2 có các ý a, b, c, d. Dưới đây là ví dụ giải cho ý a)
a) y = 3x - 2
Biểu thức này đã ở dạng y = ax + b, với a = 3 và b = -2. Vì a ≠ 0, nên đây là một hàm số bậc nhất.
b) y = x2 + 1
Biểu thức này có chứa x2, không thể biến đổi về dạng y = ax + b. Do đó, đây không phải là hàm số bậc nhất.
c) y = -5x
Biểu thức này có thể viết lại thành y = -5x + 0, với a = -5 và b = 0. Vì a ≠ 0, nên đây là một hàm số bậc nhất.
d) y + 2x = 5
Biểu thức này có thể viết lại thành y = -2x + 5, với a = -2 và b = 5. Vì a ≠ 0, nên đây là một hàm số bậc nhất.
4. Mở rộng và bài tập tương tự:
Để hiểu rõ hơn về hàm số bậc nhất, các em có thể tự giải thêm các bài tập tương tự. Ví dụ:
5. Ứng dụng của hàm số bậc nhất:
Hàm số bậc nhất có rất nhiều ứng dụng trong thực tế, ví dụ như:
6. Lưu ý khi giải bài tập về hàm số bậc nhất:
Hy vọng với bài giải chi tiết này, các em học sinh đã hiểu rõ hơn về cách giải bài tập 2.2 trang 36 SGK Toán 9 tập 1. Chúc các em học tập tốt!