Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau khám phá và tìm ra lời giải chi tiết cho mục 2 trang 84 và 85 của sách giáo khoa Toán 9 tập 1.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, rèn luyện kỹ năng giải quyết vấn đề và tự tin hơn trong quá trình học tập.
Trong mỗi trường hợp dưới đây, hãy xác định độ dài các cạnh và số đo góc ở các ô . Làm tròn số đo góc đến độ và độ dài cạnh đến hàng phần mười. Cho biết em đã sử dụng hệ thức, định lí nào để tính.
Trả lời câu hỏi Luyện tập 2 trang 85SGK Toán 9 Cùng khám phá
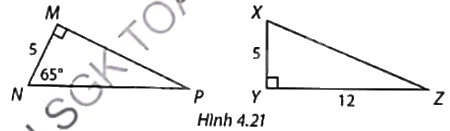
Giải các tam giác vuông MNP và XYZ trong Hình 4.21. Làm tròn số đo góc đến độ và độ dài cạnh đến hàng phần mười.
Phương pháp giải:
Tam giác MNP vuông tại M nên \(\hat P = {90^o} - \hat N\), \(MP = MN.\tan N\), \(NP = \frac{{NM}}{{\cos N}}\).
Tam giác XYZ vuông tại Y nên \(XZ = \sqrt {X{Y^2} + Y{Z^2}} \), \(\cos X = \frac{{XY}}{{XZ}}\) nên tính được góc X, \(\widehat Z = {90^o} - \widehat X\).
Lời giải chi tiết:
Tam giác MNP vuông tại M nên:
\(\widehat P = {90^o} - \widehat N = {90^o} - {65^o} = {25^o}\).
\(\begin{array}{l}MP = MN.\tan N = 5.\tan {65^o} \approx 10,7\\NP = \frac{{NM}}{{\cos N}} = \frac{5}{{\cos {{65}^o}}} = 11,8\end{array}\)
Tam giác XYZ vuông tại Y nên:
\(XZ = \sqrt {X{Y^2} + Y{Z^2}} = \sqrt {{5^2} + {{12}^2}} = 13\)
\(\cos X = \frac{{XY}}{{XZ}} = \frac{5}{{13}}\) nên \(\widehat X \approx {67^o}\).
Suy ra: \(\widehat Z = {90^o} - \widehat X \approx {23^o}\).
Trả lời câu hỏi Vận dụng 2 trang 85 SGK Toán 9 Cùng khám phá
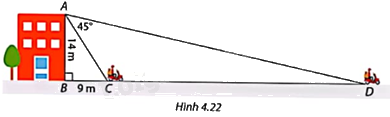
Trong Hình 4.22, một người đứng từ sân thượng tòa nhà và quan sát một người đi xe máy từ vị trí C đến vị trí D.
a) Giải tam giác vuông ABD.
b) Tính tốc độ của xe máy, biết thời gian xe đi từ C đến D là 6,5 giây. Làm tròn số đo góc đến độ và độ dài cạnh đến hàng phần mười mét.
Phương pháp giải:
a) + Tam giác ABC vuông tại B nên \(\tan BAC = \frac{{BC}}{{AB}}\), từ đó tính được góc BAC.
+ \(\widehat {BAD} = \widehat {BAC} + \widehat {CAD}\), \(\widehat D = {90^o} - \widehat {BAD}\).
+ \(AD = \frac{{AB}}{{\sin D}},BD = \frac{{AB}}{{\tan D}}\).
b) Áp dụng công thức: \(v = \frac{s}{t}\), trong đó s là quãng đường CD và t thời gian xe đi từ C đến D là 6,5 giây.
Lời giải chi tiết:
a) Tam giác ABC vuông tại B nên \(\tan BAC = \frac{{BC}}{{AB}} = \frac{9}{{14}}\) nên \(\widehat {BAC} \approx {33^o}\).
Suy ra: \(\widehat {BAD} = \widehat {BAC} + \widehat {CAD} \approx {78^o}\)
Tam giác ABD vuông tại B nên \(\widehat D = {90^o} - \widehat {BAD} \approx {12^o}\).
\(\begin{array}{l}AD = \frac{{AB}}{{\sin D}} \approx \frac{{14}}{{\sin {{12}^o}}} \approx 67,3\left( m \right),\\BD = \frac{{AB}}{{\tan D}} \approx \frac{{14}}{{\tan {{12}^o}}} \approx 65,9\left( m \right)\end{array}\)
b) \(CD = BD - BC = 65,9 - 9 = 56,9\left( m \right)\).
Tốc độ của xe máy đi từ C đến D là:
\(\frac{{56,9}}{{6,5}} \approx 8,8\left( {m/s} \right)\).
Trả lời câu hỏi Hoạt động 2 trang 84 SGK Toán 9 Cùng khám phá
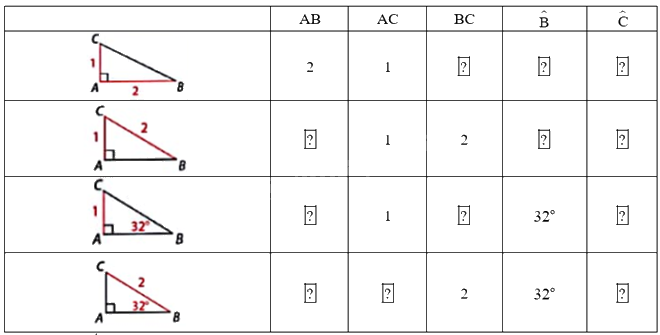
Trong mỗi trường hợp dưới đây, hãy xác định độ dài các cạnh và số đo góc ở các ô . Làm tròn số đo góc đến độ và độ dài cạnh đến hàng phần mười. Cho biết em đã sử dụng hệ thức, định lí nào để tính.
Phương pháp giải:
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
+ Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề;
+ Cạnh góc vuông còn lại nhân tang góc đối hoặc côtang góc kề.
Lời giải chi tiết:
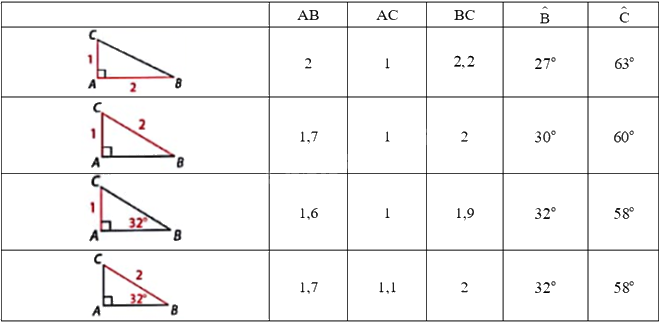
Em đã sử dụng các kiến thức:
- Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
+ Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề;
+ Cạnh góc vuông còn lại nhân tang góc đối hoặc côtang góc kề.
- Sử dụng định lí Pythagore trong tam giác vuông.
- Trong tam giác vuông có góc nhọn \(\alpha \), khi đó:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là \(\sin \alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là \(\cos \alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là \(\tan \alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là \(\cot \alpha \).
Trả lời câu hỏi Hoạt động 2 trang 84 SGK Toán 9 Cùng khám phá
Trong mỗi trường hợp dưới đây, hãy xác định độ dài các cạnh và số đo góc ở các ô . Làm tròn số đo góc đến độ và độ dài cạnh đến hàng phần mười. Cho biết em đã sử dụng hệ thức, định lí nào để tính.
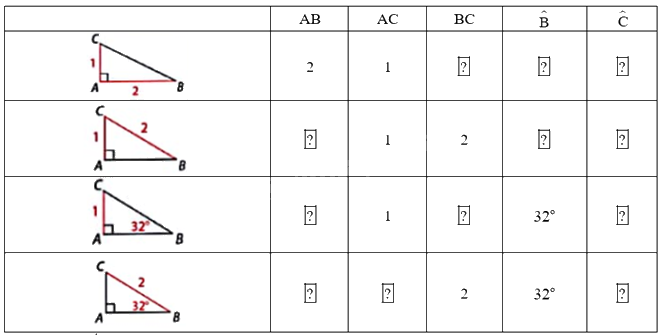
Phương pháp giải:
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
+ Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề;
+ Cạnh góc vuông còn lại nhân tang góc đối hoặc côtang góc kề.
Lời giải chi tiết:
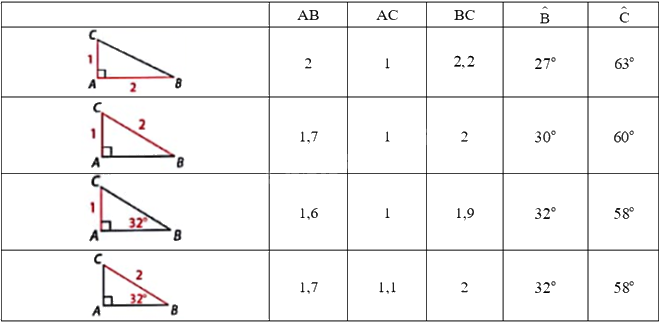
Em đã sử dụng các kiến thức:
- Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
+ Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề;
+ Cạnh góc vuông còn lại nhân tang góc đối hoặc côtang góc kề.
- Sử dụng định lí Pythagore trong tam giác vuông.
- Trong tam giác vuông có góc nhọn \(\alpha \), khi đó:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là \(\sin \alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là \(\cos \alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là \(\tan \alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là \(\cot \alpha \).
Trả lời câu hỏi Luyện tập 2 trang 85SGK Toán 9 Cùng khám phá
Giải các tam giác vuông MNP và XYZ trong Hình 4.21. Làm tròn số đo góc đến độ và độ dài cạnh đến hàng phần mười.
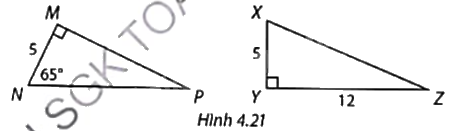
Phương pháp giải:
Tam giác MNP vuông tại M nên \(\hat P = {90^o} - \hat N\), \(MP = MN.\tan N\), \(NP = \frac{{NM}}{{\cos N}}\).
Tam giác XYZ vuông tại Y nên \(XZ = \sqrt {X{Y^2} + Y{Z^2}} \), \(\cos X = \frac{{XY}}{{XZ}}\) nên tính được góc X, \(\widehat Z = {90^o} - \widehat X\).
Lời giải chi tiết:
Tam giác MNP vuông tại M nên:
\(\widehat P = {90^o} - \widehat N = {90^o} - {65^o} = {25^o}\).
\(\begin{array}{l}MP = MN.\tan N = 5.\tan {65^o} \approx 10,7\\NP = \frac{{NM}}{{\cos N}} = \frac{5}{{\cos {{65}^o}}} = 11,8\end{array}\)
Tam giác XYZ vuông tại Y nên:
\(XZ = \sqrt {X{Y^2} + Y{Z^2}} = \sqrt {{5^2} + {{12}^2}} = 13\)
\(\cos X = \frac{{XY}}{{XZ}} = \frac{5}{{13}}\) nên \(\widehat X \approx {67^o}\).
Suy ra: \(\widehat Z = {90^o} - \widehat X \approx {23^o}\).
Trả lời câu hỏi Vận dụng 2 trang 85 SGK Toán 9 Cùng khám phá
Trong Hình 4.22, một người đứng từ sân thượng tòa nhà và quan sát một người đi xe máy từ vị trí C đến vị trí D.
a) Giải tam giác vuông ABD.
b) Tính tốc độ của xe máy, biết thời gian xe đi từ C đến D là 6,5 giây. Làm tròn số đo góc đến độ và độ dài cạnh đến hàng phần mười mét.
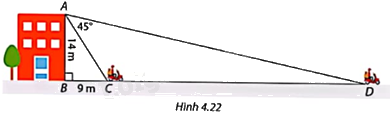
Phương pháp giải:
a) + Tam giác ABC vuông tại B nên \(\tan BAC = \frac{{BC}}{{AB}}\), từ đó tính được góc BAC.
+ \(\widehat {BAD} = \widehat {BAC} + \widehat {CAD}\), \(\widehat D = {90^o} - \widehat {BAD}\).
+ \(AD = \frac{{AB}}{{\sin D}},BD = \frac{{AB}}{{\tan D}}\).
b) Áp dụng công thức: \(v = \frac{s}{t}\), trong đó s là quãng đường CD và t thời gian xe đi từ C đến D là 6,5 giây.
Lời giải chi tiết:
a) Tam giác ABC vuông tại B nên \(\tan BAC = \frac{{BC}}{{AB}} = \frac{9}{{14}}\) nên \(\widehat {BAC} \approx {33^o}\).
Suy ra: \(\widehat {BAD} = \widehat {BAC} + \widehat {CAD} \approx {78^o}\)
Tam giác ABD vuông tại B nên \(\widehat D = {90^o} - \widehat {BAD} \approx {12^o}\).
\(\begin{array}{l}AD = \frac{{AB}}{{\sin D}} \approx \frac{{14}}{{\sin {{12}^o}}} \approx 67,3\left( m \right),\\BD = \frac{{AB}}{{\tan D}} \approx \frac{{14}}{{\tan {{12}^o}}} \approx 65,9\left( m \right)\end{array}\)
b) \(CD = BD - BC = 65,9 - 9 = 56,9\left( m \right)\).
Tốc độ của xe máy đi từ C đến D là:
\(\frac{{56,9}}{{6,5}} \approx 8,8\left( {m/s} \right)\).
Mục 2 của chương trình Toán 9 tập 1 thường tập trung vào các chủ đề như hàm số bậc nhất, đồ thị hàm số, và ứng dụng của hàm số trong giải quyết các bài toán thực tế. Việc nắm vững kiến thức trong mục này là nền tảng quan trọng để học tốt các chương tiếp theo.
Bài tập này yêu cầu học sinh xác định hàm số bậc nhất dựa trên các thông tin cho trước, vẽ đồ thị hàm số, và tìm các điểm thuộc đồ thị. Để giải bài tập này, học sinh cần nắm vững định nghĩa hàm số bậc nhất, công thức tính hệ số góc và tung độ gốc, và cách vẽ đồ thị hàm số.
Bài tập này thường liên quan đến các tình huống thực tế như tính quãng đường đi được, tính tiền lương, hoặc tính lợi nhuận. Để giải bài tập này, học sinh cần chuyển đổi các thông tin trong bài toán thành các biểu thức toán học và sử dụng hàm số bậc nhất để giải quyết.
Ví dụ, nếu một ô tô đi với vận tốc không đổi là 60km/h, thì quãng đường đi được sau t giờ là s = 60t. Đây là một hàm số bậc nhất với hệ số góc là 60 và tung độ gốc là 0.
Bài tập này yêu cầu học sinh tìm tọa độ giao điểm của hai đường thẳng. Để giải bài tập này, học sinh cần viết phương trình của hai đường thẳng và giải hệ phương trình hai ẩn để tìm tọa độ giao điểm.
Ví dụ, để tìm giao điểm của hai đường thẳng y = 2x + 1 và y = -x + 4, ta giải hệ phương trình sau:
Thay y = 2x + 1 vào phương trình thứ hai, ta được: 2x + 1 = -x + 4. Giải phương trình này, ta được x = 1. Thay x = 1 vào phương trình y = 2x + 1, ta được y = 3. Vậy giao điểm của hai đường thẳng là (1, 3).
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 9:
Hy vọng rằng với những hướng dẫn chi tiết trên, các em học sinh đã có thể tự tin giải quyết các bài tập trong mục 2 trang 84, 85 SGK Toán 9 tập 1. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!