Góc nội tiếp là một trong những kiến thức quan trọng của chương trình Toán 9, đóng vai trò then chốt trong việc giải các bài toán hình học. Bài viết này tại giaitoan.edu.vn sẽ cung cấp cho bạn một cách đầy đủ và dễ hiểu về lý thuyết góc nội tiếp, cùng với các ví dụ minh họa và bài tập thực hành.
Chúng tôi cam kết mang đến cho bạn trải nghiệm học toán online hiệu quả và thú vị.
1. Góc nội tiếp Định nghĩa Góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây của đường tròn được gọi là một góc nội tiếp của đường tròn.
1. Góc nội tiếp
Định nghĩa
Góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây của đường tròn được gọi là một góc nội tiếp của đường tròn. |
Lưu ý: Cung bị chắn bởi một góc nội tiếp là cung nằm trong góc nội tiếp đó.
2. Liên hệ giữa số đo của góc nội tiếp và số đo cung
Số đo góc nội tiếp
Trong một đường tròn, số đo của góc nội tiếp bằng một nửa số đo cung bị chắn bởi góc đó. |
Ví dụ:
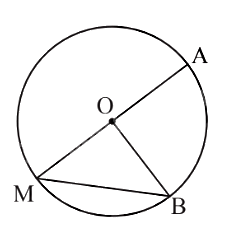
\(\widehat {AMB}\)là góc nội tiếp chắn $\overset\frown{AB}$ trên đường tròn (O) nên \(\widehat {AMB} = \frac{1}{2}\)sđ$\overset\frown{AB}$.
Nhận xét: Trong một đường tròn:
- Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
- Góc nội tiếp nhỏ hơn hoặc bằng \({90^o}\) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
Góc nội tiếp chắn nửa đường tròn là góc vuông.
Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai điểm khác nhau trên đường tròn. Hiểu rõ về góc nội tiếp là nền tảng để giải quyết nhiều bài toán hình học quan trọng trong chương trình Toán 9. Bài viết này sẽ đi sâu vào định nghĩa, tính chất, hệ quả và các ứng dụng thực tế của góc nội tiếp.
Góc nội tiếp của một đường tròn là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai điểm khác nhau trên đường tròn. Ví dụ, góc ∠ABC trong hình vẽ dưới đây là một góc nội tiếp của đường tròn (O).

Tính chất quan trọng nhất của góc nội tiếp là:
Cụ thể, nếu ∠ABC là góc nội tiếp chắn cung AC thì ∠ABC = 1/2 * số đo cung AC.
Từ tính chất trên, ta có một số hệ quả quan trọng:
Các bài tập về góc nội tiếp thường xoay quanh các chủ đề sau:
Ví dụ 1: Cho đường tròn (O) có bán kính 5cm. Trên đường tròn lấy hai điểm A và B sao cho số đo cung AB bằng 60°. Tính số đo góc nội tiếp ∠ACB (C là điểm bất kỳ trên đường tròn không trùng với A và B).
Giải: Vì ∠ACB là góc nội tiếp chắn cung AB nên ∠ACB = 1/2 * số đo cung AB = 1/2 * 60° = 30°.
Ví dụ 2: Cho tam giác ABC nội tiếp đường tròn (O). Biết ∠BAC = 80° và ∠ABC = 60°. Tính số đo góc ∠BOC.
Giải: Ta có ∠ACB = 180° - ∠BAC - ∠ABC = 180° - 80° - 60° = 40°. Vì ∠BOC là góc ở tâm chắn cung BC nên ∠BOC = 2 * ∠BAC = 2 * 80° = 160°.
Góc tạo bởi tiếp tuyến và dây cung tại điểm tiếp xúc bằng nửa số đo cung bị chắn. Điều này có thể được sử dụng để giải quyết các bài toán liên quan đến tiếp tuyến và dây cung.
Để nắm vững kiến thức về góc nội tiếp, bạn nên thực hành giải nhiều bài tập khác nhau. Dưới đây là một số bài tập gợi ý:
Lý thuyết góc nội tiếp là một phần quan trọng của chương trình Toán 9. Việc nắm vững lý thuyết và rèn luyện kỹ năng giải bài tập sẽ giúp bạn tự tin hơn trong các kỳ thi và ứng dụng kiến thức vào thực tế. Hãy truy cập giaitoan.edu.vn để học toán online hiệu quả và khám phá thêm nhiều kiến thức thú vị khác!
| Khái niệm | Định nghĩa |
|---|---|
| Góc nội tiếp | Góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai điểm khác nhau trên đường tròn. |
| Cung bị chắn | Cung nằm giữa hai điểm trên đường tròn mà hai cạnh của góc nội tiếp chứa. |