Chào mừng các em học sinh đến với bài giải bài tập 5.15 trang 110 SGK Toán 9 tập 1 tại giaitoan.edu.vn. Bài tập này thuộc chương Hàm số bậc nhất và là một phần quan trọng trong việc củng cố kiến thức về hàm số.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và áp dụng vào các bài tập tương tự. Ngoài ra, chúng tôi còn có các bài giảng video và tài liệu tham khảo hữu ích khác.
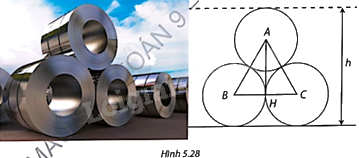
Trong Hình 5.28, các cuộn thép được đặt chồng lên nhau. Đường kính của mỗi cuộn thép là 1,2m. Gọi A, B, C lần lượt là tâm của mặt cắt các cuộn thép, H là tiếp điểm của hai cuộn thép phía dưới. a) Chứng minh \(\Delta ABC\) là tam giác đều và tính độ dài AH. b) Tính khoảng cách từ B và C đến mặt đất. c) Tính chiều cao h của khối ba cuộn thép.
Đề bài
Trong Hình 5.28, các cuộn thép được đặt chồng lên nhau. Đường kính của mỗi cuộn thép là 1,2m. Gọi A, B, C lần lượt là tâm của mặt cắt các cuộn thép, H là tiếp điểm của hai cuộn thép phía dưới.
a) Chứng minh \(\Delta ABC\) là tam giác đều và tính độ dài AH.
b) Tính khoảng cách từ B và C đến mặt đất.
c) Tính chiều cao h của khối ba cuộn thép.
Phương pháp giải - Xem chi tiết
a) + Gọi I là tiếp điểm của mặt cắt của các cuộn thép tâm A và tâm C, K là tiếp điểm của mặt cắt của các cuộn thép tâm A và tâm B.
+ Tính bán kính của các đường tròn (A), (B), (C).
+ Từ đó tính được \(AB = BC = AC\) nên tam giác ABC đều.
+ Chứng minh AH là đường trung tuyến đồng thời là đường cao trong tam giác ABC đều.
+ Áp dụng định lí Pythagore để tính AH.
b) Đường tròn tâm (B), (C) tiếp xúc với mặt đất nên khoảng cách từ B, C đến mặt đất bằng bán kính của đường tròn tâm (B), (C).
c) + Chiều cao của ba cuộn thép bằng tổng đường kính của hai đường tròn tâm A và tâm C.
Lời giải chi tiết
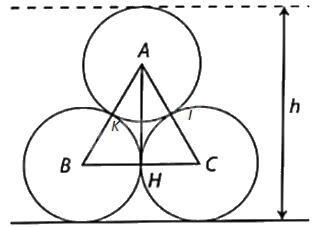
Gọi I là tiếp điểm của mặt cắt của các cuộn thép tâm A và tâm C, K là tiếp điểm của mặt cắt của các cuộn thép tâm A và tâm B.
a) Vì AI, AK là bán kính đường tròn (A) nên
\(AI = AK = \frac{{1,2}}{2} = 0,6m\).
Vì BH, BK là bán kính đường tròn (B) nên
\(BH = BK = \frac{{1,2}}{2} = 0,6m\).
Vì CI, CH là bán kính đường tròn (C) nên
\(CI = CH = \frac{{1,2}}{2} = 0,6m\).
Vì các cuộn thép tâm A, B, C đặt chồng lên nhau nên các mặt cắt của các cuộn thép tâm A, B, C tiếp xúc ngoài nhau.
Do đó, \(AC = AI + IC = 1,2m,BC = BH + HC = 1,2m,AB = BK + AK = 1,2m\)
Suy ra: \(AB = BC = AC\).
Vậy \(\Delta ABC\) là tam giác đều
Mà AH là đường trung tuyến của tam giác ABC (vì \(BH = HC\)) nên AH là đường cao của tam giác ABC. Suy ra, tam giác AHC vuông tại H.
Do đó, \(A{H^2} + H{C^2} = A{C^2}\) (định lí Pythagore), suy ra
\(AH = \sqrt {A{C^2} - A{H^2}} = \sqrt {1,{2^2} - 0,{6^2}} = \frac{{3\sqrt 3 }}{5}\left( m \right)\)
b) Vì đường tròn tâm (B), (C) tiếp xúc với mặt đất nên khoảng cách từ B, C đến mặt đất bằng bán kính của đường tròn tâm (B), (C).
Do đó, khoảng cách từ B và C đến mặt đất đều bằng 0,6m.
c) Vì các cuộn thép tâm A, B, C tiếp xúc ngoài nhau nên chiều cao h của khối ba cuộn thép là: \(h = 1,2 + 1,2 = 2,4\left( m \right)\)
Bài tập 5.15 trang 110 SGK Toán 9 tập 1 yêu cầu tìm phương trình đường thẳng là tiếp tuyến của đồ thị hàm số y = -2x + 3 tại điểm có hoành độ x = 1.
Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:
Bài toán yêu cầu tìm phương trình đường thẳng tiếp xúc với đồ thị hàm số y = -2x + 3 tại điểm có hoành độ x = 1. Điều này có nghĩa là đường thẳng cần tìm phải đi qua điểm có tọa độ (1, y) và có hệ số góc bằng -2.
Bước 1: Tìm tung độ của điểm tiếp xúc
Thay x = 1 vào phương trình hàm số y = -2x + 3, ta được:
y = -2 * 1 + 3 = 1
Vậy điểm tiếp xúc có tọa độ là (1, 1).
Bước 2: Viết phương trình đường thẳng tiếp tuyến
Vì đường thẳng tiếp tuyến có hệ số góc a = -2 và đi qua điểm (1, 1), ta có thể viết phương trình đường thẳng theo dạng:
y - y1 = a(x - x1)
Thay a = -2, x1 = 1, y1 = 1 vào phương trình, ta được:
y - 1 = -2(x - 1)
y - 1 = -2x + 2
y = -2x + 3
Vậy phương trình đường thẳng tiếp tuyến là y = -2x + 3.
Phương trình đường thẳng là tiếp tuyến của đồ thị hàm số y = -2x + 3 tại điểm có hoành độ x = 1 là y = -2x + 3.
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự sau:
Các em có thể tìm hiểu thêm về ứng dụng của tiếp tuyến trong việc giải các bài toán liên quan đến tối ưu hóa và tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số.
Ngoài ra, các em cũng có thể tham khảo thêm các tài liệu và bài giảng online khác để nắm vững kiến thức về hàm số và đồ thị hàm số.
Lưu ý: Bài giải trên chỉ mang tính chất tham khảo. Các em nên tự mình suy nghĩ và giải bài tập để hiểu rõ hơn về phương pháp giải.