Chào mừng các em học sinh đến với bài giải bài tập 5.40 trang 128 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương Hàm số bậc nhất và là một phần quan trọng trong việc củng cố kiến thức về hàm số.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và áp dụng vào các bài tập tương tự.
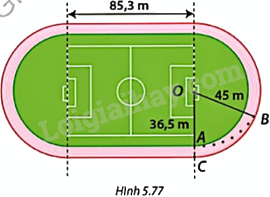
Trong Hình 5.77, mỗi làn chạy của sân vận động được thiết kế gồm hai phần là đường chạy thẳng và hai phần có dạng nửa đường tròn. Trong một cuộc thi điền kinh, vận động viên ở làn trong cùng xuất phát từ vị trí điểm A, chạy ngược chiều kim đồng hồ đúng một vòng và về đích ở điểm A. a) Tính cự li chạy của cuộc thi (tổng quãng đường vận động viên phải chạy). b) Để đảm bảo cự li chạy như nhau, vận động viên ở làn ngoài cùng không chạy đúng một vòng mà xuất phát từ vị trí điểm B và về đích ở điểm
Đề bài
Trong Hình 5.77, mỗi làn chạy của sân vận động được thiết kế gồm hai phần là đường chạy thẳng và hai phần có dạng nửa đường tròn. Trong một cuộc thi điền kinh, vận động viên ở làn trong cùng xuất phát từ vị trí điểm A, chạy ngược chiều kim đồng hồ đúng một vòng và về đích ở điểm A.
a) Tính cự li chạy của cuộc thi (tổng quãng đường vận động viên phải chạy).
b) Để đảm bảo cự li chạy như nhau, vận động viên ở làn ngoài cùng không chạy đúng một vòng mà xuất phát từ vị trí điểm B và về đích ở điểm C. Xác định số đo góc COB.
Phương pháp giải - Xem chi tiết
a) Tổng quãng đường vận động viên phải chạy bằng tổng độ dài 2 đường chạy thẳng dài, mỗi đường dài 85,3m và hai phần có dạng nửa đường tròn có bán kính 36,5m.
b) + Độ dài cung CB bằng độ dài làn ngoài cùng – tổng cự li chạy của cuộc thi.
+ Áp dụng công thức tính độ dài cung CB, để tính số đo cung CB nhỏ, từ đó tính được góc COB.
Lời giải chi tiết
a) Độ dài hai nửa đường tròn bán kính 36,5m là:
\({C_1} = 2.\pi .36,5 = 73\pi \left( m \right)\)
Tổng cự li chạy của cuộc là:
\(C = 73\pi + 85,3.2 = 73\pi + 170,6\left( m \right)\)
b) Độ dài làn ngoài cùng là:
\({C_2} = 2\pi .45 + 85,3.2 = 90\pi + 170,6\left( m \right)\)
Độ dài cung CB là:
\({C_3} = {C_2} - {C_1} = 90\pi + 170,6 - 73\pi - 170,6 = 17\pi \left( {cm} \right)\)
Do đó, $17\pi =\frac{\pi .45.sđ\overset\frown{BC}}{180}$, suy ra: $sđ\overset\frown{BC}={{68}^{o}}$
Vì BOC là góc ở tâm chắn cung BC nhỏ nên $\widehat{BOC}=sđ\overset\frown{BC}={{68}^{o}}$
Bài tập 5.40 trang 128 SGK Toán 9 tập 1 yêu cầu chúng ta tìm hiểu về hàm số bậc nhất và ứng dụng của nó trong việc giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản về hàm số, bao gồm tập xác định, tập giá trị, và cách biểu diễn hàm số trên mặt phẳng tọa độ.
Trước khi đi vào giải bài tập cụ thể, hãy cùng nhau ôn lại một số kiến thức lý thuyết quan trọng:
Bài tập 5.40 thường yêu cầu chúng ta:
Giả sử bài tập 5.40 có nội dung như sau: “Cho hàm số y = 2x - 3. Hãy xác định hệ số góc và tung độ gốc của hàm số. Vẽ đồ thị hàm số.”
Lời giải:
Ngoài bài tập 5.40, còn rất nhiều bài tập tương tự liên quan đến hàm số bậc nhất. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải:
Hàm số bậc nhất có rất nhiều ứng dụng trong thực tế, ví dụ như:
Để nắm vững kiến thức về hàm số bậc nhất, các em nên luyện tập thêm các bài tập khác trong SGK và các tài liệu tham khảo. Hãy tìm kiếm các bài tập có mức độ khó tăng dần để thử thách bản thân và nâng cao kỹ năng giải toán.
Bài tập 5.40 trang 128 SGK Toán 9 tập 1 là một bài tập quan trọng giúp các em hiểu rõ hơn về hàm số bậc nhất và ứng dụng của nó. Hy vọng với lời giải chi tiết và các phương pháp giải đã trình bày, các em sẽ tự tin hơn khi giải các bài tập tương tự.