Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho mục 2 trang 44, 45 SGK Toán 9 tập 2. Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán và đạt kết quả tốt trong môn Toán.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn bài giải một cách cẩn thận, kèm theo các bước giải thích rõ ràng, giúp các em hiểu sâu sắc bản chất của bài toán.
Cho các đa giác trong Bảng 8.1. So sánh các cạnh và các góc của mỗi đa giác, cho biết các đa giác ở cột B có đặc điểm gì khác so với đa giác tương ứng ở cột A.
Trả lời câu hỏi Luyện tập 2 trang 45SGK Toán 9 Cùng khám phá
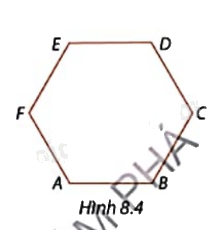
Tính số đo các góc B và E của lục giác đều trong Hình 8.4, biết \(\widehat A = {120^o}\).
Phương pháp giải:
Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
Lời giải chi tiết:
Ta có hình lục giác ABCDEF đều nên các góc bằng nhau
Suy ra \(\widehat B = \widehat E = \widehat A = {120^o}\).
Trả lời câu hỏi Vận dụng trang 45 SGK Toán 9 Cùng khám phá
Gọi tên các đa giác đều có trong Hình 8.6.

Phương pháp giải:
Nhìn hình và gọi tên.
Lời giải chi tiết:
a) Tam giác đều
b) Không phải đa giác đều
c) Lục giác đều
d) Không phải đa giác đều
e) Bát giác đều
f) Hình vuông.
Trả lời câu hỏi Hoạt động 3 trang 44 SGK Toán 9 Cùng khám phá
Cho các đa giác trong Bảng 8.1. So sánh các cạnh và các góc của mỗi đa giác, cho biết các đa giác ở cột B có đặc điểm gì khác so với đa giác tương ứng ở cột A.

Phương pháp giải:
Nhìn hình và nhận xét.
Lời giải chi tiết:
Các đa ở hình B có tất cả các cạnh bằng nhau và các góc bằng nhau.
Trả lời câu hỏi Hoạt động 3 trang 44 SGK Toán 9 Cùng khám phá
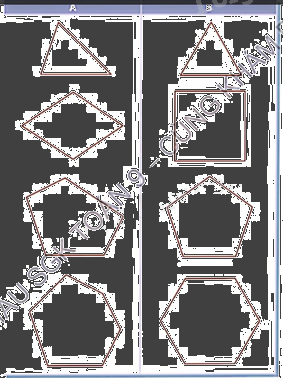
Cho các đa giác trong Bảng 8.1. So sánh các cạnh và các góc của mỗi đa giác, cho biết các đa giác ở cột B có đặc điểm gì khác so với đa giác tương ứng ở cột A.
Phương pháp giải:
Nhìn hình và nhận xét.
Lời giải chi tiết:
Các đa ở hình B có tất cả các cạnh bằng nhau và các góc bằng nhau.
Trả lời câu hỏi Luyện tập 2 trang 45SGK Toán 9 Cùng khám phá
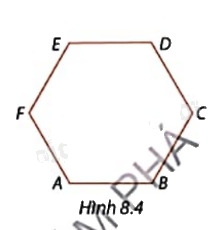
Tính số đo các góc B và E của lục giác đều trong Hình 8.4, biết \(\widehat A = {120^o}\).
Phương pháp giải:
Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
Lời giải chi tiết:
Ta có hình lục giác ABCDEF đều nên các góc bằng nhau
Suy ra \(\widehat B = \widehat E = \widehat A = {120^o}\).
Trả lời câu hỏi Vận dụng trang 45 SGK Toán 9 Cùng khám phá
Gọi tên các đa giác đều có trong Hình 8.6.

Phương pháp giải:
Nhìn hình và gọi tên.
Lời giải chi tiết:
a) Tam giác đều
b) Không phải đa giác đều
c) Lục giác đều
d) Không phải đa giác đều
e) Bát giác đều
f) Hình vuông.
Mục 2 trang 44, 45 SGK Toán 9 tập 2 thường xoay quanh các chủ đề về hàm số bậc nhất, hàm số bậc hai, và các ứng dụng của chúng. Các bài tập trong mục này thường yêu cầu học sinh vận dụng kiến thức về định nghĩa, tính chất, đồ thị của hàm số để giải quyết các bài toán thực tế.
Bài tập này thường yêu cầu học sinh xác định xem một biểu thức có phải là hàm số hay không, và nếu có thì xác định tập xác định và tập giá trị của hàm số đó. Để giải bài tập này, học sinh cần nắm vững định nghĩa về hàm số và các điều kiện để một biểu thức trở thành hàm số.
Bài tập này yêu cầu học sinh vẽ đồ thị của một hàm số cho trước. Để vẽ đồ thị, học sinh cần xác định một số điểm thuộc đồ thị, sau đó nối các điểm này lại với nhau. Ngoài ra, học sinh cũng cần chú ý đến các yếu tố như hệ số góc, giao điểm với các trục tọa độ để vẽ đồ thị chính xác.
Bài tập này yêu cầu học sinh tìm tọa độ giao điểm của hai đường thẳng. Để giải bài tập này, học sinh cần viết phương trình của hai đường thẳng, sau đó giải hệ phương trình để tìm tọa độ giao điểm.
Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số để giải quyết các bài toán thực tế, ví dụ như tính quãng đường, vận tốc, thời gian, hoặc tính lợi nhuận, chi phí. Để giải bài tập này, học sinh cần phân tích bài toán, xác định các yếu tố liên quan đến hàm số, và xây dựng phương trình hàm số phù hợp.
Bài tập: Cho hàm số y = 2x + 1. Hãy tìm tọa độ giao điểm của đường thẳng này với đường thẳng y = -x + 4.
Giải:
Để tìm tọa độ giao điểm, ta giải hệ phương trình:
Thay y = 2x + 1 vào phương trình thứ hai, ta được:
2x + 1 = -x + 4
3x = 3
x = 1
Thay x = 1 vào phương trình y = 2x + 1, ta được:
y = 2(1) + 1 = 3
Vậy tọa độ giao điểm của hai đường thẳng là (1; 3).
Để học tốt môn Toán, đặc biệt là phần hàm số, các em cần nắm vững kiến thức cơ bản, luyện tập thường xuyên và tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè khi gặp khó khăn. Chúc các em học tập tốt!
| Công thức | Mô tả |
|---|---|
| y = ax + b | Hàm số bậc nhất |
| y = ax2 + bx + c | Hàm số bậc hai |