Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Ở bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 1 trang 115, 116, 117 sách giáo khoa Toán 9 tập 1.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, nắm vững phương pháp giải và tự tin làm bài tập.
Cắt một hình tròn bằng giấy và gấp làm hai, làm tư, làm tám như trong Hình 5.45. 1. Cho biết giao điểm O của các đường gấp ở đâu trong hình tròn? 2. Các đường gấp chia hình tròn thành nhiều phần. Trong mỗi trường hợp, hãy: a) Cho biết khi đường tròn (O) được gấp lại, các cung của đường tròn nằm trong các phần chồng khít lên nhau không? b) So sánh số đo các góc đỉnh O trong mỗi phần và tính tổng số đo các góc đỉnh O trong tất cả các phần.
Trả lời câu hỏi Hoạt động 1 trang 115SGK Toán 9 Cùng khám phá
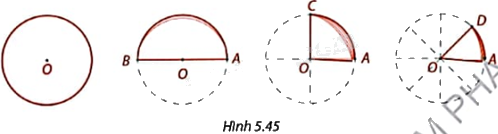
Cắt một hình tròn bằng giấy và gấp làm hai, làm tư, làm tám như trong Hình 5.45.
1. Cho biết giao điểm O của các đường gấp ở đâu trong hình tròn?
2. Các đường gấp chia hình tròn thành nhiều phần. Trong mỗi trường hợp, hãy:
a) Cho biết khi đường tròn (O) được gấp lại, các cung của đường tròn nằm trong các phần chồng khít lên nhau không?
b) So sánh số đo các góc đỉnh O trong mỗi phần và tính tổng số đo các góc đỉnh O trong tất cả các phần
Phương pháp giải:
Quan sát hình đã gấp rồi rút ra kết luận.
Lời giải chi tiết:
1. Giao điểm O của các đường gấp là tâm của hình tròn.
2. a) Khi đường tròn (O) được gấp lại, các cung của đường tròn nằm trong các phần chồng khít lên nhau.
b) + Khi gấp hình tròn làm hai: Số đo các góc ở đỉnh O trong mỗi phần bằng nhau và bằng 180 độ.
Tổng số đo của tất cả các góc đỉnh O đều bằng 360 độ.
+ Khi gấp hình tròn làm tư: Số đo các góc ở đỉnh O trong mỗi phần bằng nhau và bằng 90 độ.
Tổng số đo của tất cả các góc đỉnh O đều bằng 360 độ.
+ Khi gấp hình tròn làm tám: Số đo các góc ở đỉnh O trong mỗi phần bằng nhau và bằng 45 độ.
Tổng số đo của tất cả các góc đỉnh O đều bằng 360 độ.
Trả lời câu hỏi Luyện tập 1 trang 117 SGK Toán 9 Cùng khám phá
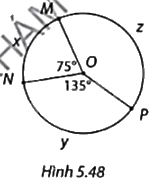
Xác định số đo của các cung MxN, NyP và MzP trong Hình 5.48.
Phương pháp giải:
Số đo của cung nhỏ là số đo của góc ở tâm chắn cung đó.
Lời giải chi tiết:
Ta có: $\widehat{MOP}$ $={{360}^{o}}-\widehat{MON}-\widehat{NOP}$ $={{360}^{o}}-{{75}^{o}}-{{135}^{o}}$ $={{150}^{o}}$.
Góc MON là góc ở tâm chắn cung MxN nên $sđ\overset\frown{MxN}$ $=\widehat{MON}$ $={{75}^{o}}$.
Góc PON là góc ở tâm chắn cung NyP nên $sđ\overset\frown{NyP}$ $=\widehat{PON}$ $={{135}^{o}}$.
Góc MOP là góc ở tâm chắn cung MzP nên $sđ\overset\frown{MzP}$ $=\widehat{MOP}$ $={{150}^{o}}$.
Trả lời câu hỏi Hoạt động 1 trang 115SGK Toán 9 Cùng khám phá
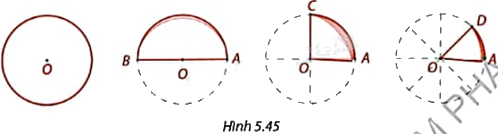
Cắt một hình tròn bằng giấy và gấp làm hai, làm tư, làm tám như trong Hình 5.45.
1. Cho biết giao điểm O của các đường gấp ở đâu trong hình tròn?
2. Các đường gấp chia hình tròn thành nhiều phần. Trong mỗi trường hợp, hãy:
a) Cho biết khi đường tròn (O) được gấp lại, các cung của đường tròn nằm trong các phần chồng khít lên nhau không?
b) So sánh số đo các góc đỉnh O trong mỗi phần và tính tổng số đo các góc đỉnh O trong tất cả các phần
Phương pháp giải:
Quan sát hình đã gấp rồi rút ra kết luận.
Lời giải chi tiết:
1. Giao điểm O của các đường gấp là tâm của hình tròn.
2. a) Khi đường tròn (O) được gấp lại, các cung của đường tròn nằm trong các phần chồng khít lên nhau.
b) + Khi gấp hình tròn làm hai: Số đo các góc ở đỉnh O trong mỗi phần bằng nhau và bằng 180 độ.
Tổng số đo của tất cả các góc đỉnh O đều bằng 360 độ.
+ Khi gấp hình tròn làm tư: Số đo các góc ở đỉnh O trong mỗi phần bằng nhau và bằng 90 độ.
Tổng số đo của tất cả các góc đỉnh O đều bằng 360 độ.
+ Khi gấp hình tròn làm tám: Số đo các góc ở đỉnh O trong mỗi phần bằng nhau và bằng 45 độ.
Tổng số đo của tất cả các góc đỉnh O đều bằng 360 độ.
Trả lời câu hỏi Luyện tập 1 trang 117 SGK Toán 9 Cùng khám phá
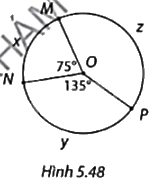
Xác định số đo của các cung MxN, NyP và MzP trong Hình 5.48.
Phương pháp giải:
Số đo của cung nhỏ là số đo của góc ở tâm chắn cung đó.
Lời giải chi tiết:
Ta có: $\widehat{MOP}$ $={{360}^{o}}-\widehat{MON}-\widehat{NOP}$ $={{360}^{o}}-{{75}^{o}}-{{135}^{o}}$ $={{150}^{o}}$.
Góc MON là góc ở tâm chắn cung MxN nên $sđ\overset\frown{MxN}$ $=\widehat{MON}$ $={{75}^{o}}$.
Góc PON là góc ở tâm chắn cung NyP nên $sđ\overset\frown{NyP}$ $=\widehat{PON}$ $={{135}^{o}}$.
Góc MOP là góc ở tâm chắn cung MzP nên $sđ\overset\frown{MzP}$ $=\widehat{MOP}$ $={{150}^{o}}$.
Mục 1 của chương trình Toán 9 tập 1 thường tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc nhất. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài tập này thường yêu cầu học sinh xác định các yếu tố của hàm số bậc nhất (hệ số a, b), vẽ đồ thị hàm số, tìm giao điểm của đồ thị hàm số với các trục tọa độ, và giải các bài toán liên quan đến ứng dụng của hàm số bậc nhất.
Bài tập này thường bao gồm các dạng bài tập khác nhau như:
Bài tập này thường kết hợp các kiến thức và kỹ năng đã học trong các bài tập trước để giải quyết các bài toán phức tạp hơn. Học sinh cần phải có khả năng phân tích bài toán, lựa chọn phương pháp giải phù hợp và thực hiện các phép tính chính xác.
Ví dụ: Cho hàm số y = 2x + 1. Hãy tìm tọa độ giao điểm của đồ thị hàm số với trục Ox.
Giải:
Để tìm tọa độ giao điểm của đồ thị hàm số với trục Ox, ta cần giải phương trình 2x + 1 = 0. Giải phương trình, ta được x = -1/2. Vậy tọa độ giao điểm của đồ thị hàm số với trục Ox là (-1/2, 0).
Khi giải bài tập về hàm số bậc nhất, học sinh cần lưu ý:
Hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh đã có thể tự tin giải các bài tập trong mục 1 trang 115, 116, 117 SGK Toán 9 tập 1. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!