Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 2 trang 112, 113, 114 sách giáo khoa Toán 9 tập 1.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, nắm vững phương pháp giải và tự tin làm bài tập.
Vẽ đường tròn (O) và lấy hai điểm A, B thuộc (O) (AB không là đường kính). Vẽ tiếp tuyến tại A và B cắt nhau tại M. Em hãy đo và so sánh: a) MA và MB; b) \(\widehat {AMO}\) và \(\widehat {BMO}\); c) \(\widehat {AOM}\) và \(\widehat {BOM}\).
Trả lời câu hỏi Hoạt động 3 trang 112 SGK Toán 9 Cùng khám phá
Vẽ đường tròn (O) và lấy hai điểm A, B thuộc (O) (AB không là đường kính). Vẽ tiếp tuyến tại A và B cắt nhau tại M. Em hãy đo và so sánh:
a) MA và MB;
b) \(\widehat {AMO}\) và \(\widehat {BMO}\);
c) \(\widehat {AOM}\) và \(\widehat {BOM}\).
Phương pháp giải:
Đo hình và đưa ra kết luận.
Lời giải chi tiết:
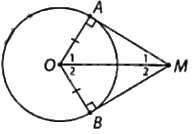
Tiến hành đo và so sánh ta có:
a) \(MA = MB\)
b) \(\widehat {AMO} = \widehat {BMO}\)
c) \(\widehat {AOM} = \widehat {BOM}\)
Trả lời câu hỏi Luyện tập 3 trang 113 SGK Toán 9 Cùng khám phá
Trong Hình 5.38, ZX và ZY là hai tiếp tuyến của đường tròn tâm O với tiếp điểm lần lượt là X và Y. Xác định số đo \(\widehat {XOY}\) và độ dài YZ.
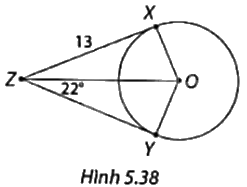
Phương pháp giải:
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:
+ Điểm đó cách đều hai tiếp điểm;
+ Tia kẻ từ tâm đi qua điểm đó là tia phân giác góc tạo bởi hai bán kính đi qua các tiếp điểm.
Lời giải chi tiết:
ZX và ZY là hai tiếp tuyến của đường tròn tâm O với tiếp điểm lần lượt là X và Ynên
+ \(YZ = ZX = 13\)
+ OZ là tia phân giác góc XOY nên \(\widehat {XOY} = 2\widehat {ZOY}\)
Vì ZY là tiếp tuyến của đường tròn tâm O nên \(ZY \bot OY\) nên tam giác ZOY vuông tại Y.
Do đó, \(\widehat {ZOY} = {90^o} - \widehat {YZO} = {90^o} - {22^o} = {68^o}\)
Vậy \(\widehat {XOY} = 2\widehat {ZOY} = {2.68^o} = {136^o}\).
Trả lời câu hỏi Vận dụng trang 114 SGK Toán 9 Cùng khám phá
Trong Hình 5.39, người ta dùng một đoạn dây gắn vào hai điểm A, B trên viền một chiếc gương tròn để treo gương vào điểm M. Biết tổng độ dài dây là 82cm, \(\widehat {AMB} = {52^o}\) và MA, MB tiếp xúc với viền gương. Tính đường kính của gương. Làm tròn kết quả đến đơn vị centimét.
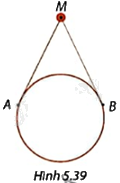
Phương pháp giải:
+ Vì MA, MB là tiếp tuyến của (O) nên \(\widehat {AMO} = \widehat {BMO} = \frac{1}{2}\widehat {AMB}\) và \(MA = MB\).
+ Tam giác AMO vuông tại A nên \(OA = AM.\tan AMO\), từ đó tính được OA.
+ Đường kính của gương là: \(2OA\).
Lời giải chi tiết:
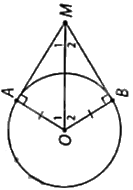
Gọi O là tâm của chiếc gương.
Vì MA, MB là tiếp tuyến của (O) nên:
+ MO là tia phân giác góc AMB, suy ra:
\(\widehat {AMO} = \widehat {BMO} = \frac{1}{2}\widehat {AMB} = \frac{1}{2}{.52^o} = {26^o}\).
+ \(MA = MB = \frac{{82}}{2} = 41cm\).
Vì MA là tiếp tuyến của (O) nên \(MA \bot AO\). Do đó, tam giác AMO vuông tại A.
Suy ra: \(OA = AM.\tan AMO = 41.\tan {26^o}\).
Vậy đường kính của gương là: \(2OA = 2.41.\tan {26^o} \approx 40\left( {cm} \right)\)
Trả lời câu hỏi Hoạt động 3 trang 112 SGK Toán 9 Cùng khám phá
Vẽ đường tròn (O) và lấy hai điểm A, B thuộc (O) (AB không là đường kính). Vẽ tiếp tuyến tại A và B cắt nhau tại M. Em hãy đo và so sánh:
a) MA và MB;
b) \(\widehat {AMO}\) và \(\widehat {BMO}\);
c) \(\widehat {AOM}\) và \(\widehat {BOM}\).
Phương pháp giải:
Đo hình và đưa ra kết luận.
Lời giải chi tiết:
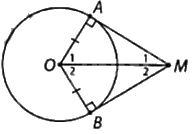
Tiến hành đo và so sánh ta có:
a) \(MA = MB\)
b) \(\widehat {AMO} = \widehat {BMO}\)
c) \(\widehat {AOM} = \widehat {BOM}\)
Trả lời câu hỏi Luyện tập 3 trang 113 SGK Toán 9 Cùng khám phá
Trong Hình 5.38, ZX và ZY là hai tiếp tuyến của đường tròn tâm O với tiếp điểm lần lượt là X và Y. Xác định số đo \(\widehat {XOY}\) và độ dài YZ.
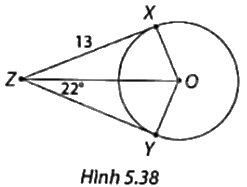
Phương pháp giải:
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:
+ Điểm đó cách đều hai tiếp điểm;
+ Tia kẻ từ tâm đi qua điểm đó là tia phân giác góc tạo bởi hai bán kính đi qua các tiếp điểm.
Lời giải chi tiết:
ZX và ZY là hai tiếp tuyến của đường tròn tâm O với tiếp điểm lần lượt là X và Ynên
+ \(YZ = ZX = 13\)
+ OZ là tia phân giác góc XOY nên \(\widehat {XOY} = 2\widehat {ZOY}\)
Vì ZY là tiếp tuyến của đường tròn tâm O nên \(ZY \bot OY\) nên tam giác ZOY vuông tại Y.
Do đó, \(\widehat {ZOY} = {90^o} - \widehat {YZO} = {90^o} - {22^o} = {68^o}\)
Vậy \(\widehat {XOY} = 2\widehat {ZOY} = {2.68^o} = {136^o}\).
Trả lời câu hỏi Vận dụng trang 114 SGK Toán 9 Cùng khám phá
Trong Hình 5.39, người ta dùng một đoạn dây gắn vào hai điểm A, B trên viền một chiếc gương tròn để treo gương vào điểm M. Biết tổng độ dài dây là 82cm, \(\widehat {AMB} = {52^o}\) và MA, MB tiếp xúc với viền gương. Tính đường kính của gương. Làm tròn kết quả đến đơn vị centimét.
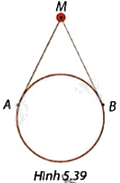
Phương pháp giải:
+ Vì MA, MB là tiếp tuyến của (O) nên \(\widehat {AMO} = \widehat {BMO} = \frac{1}{2}\widehat {AMB}\) và \(MA = MB\).
+ Tam giác AMO vuông tại A nên \(OA = AM.\tan AMO\), từ đó tính được OA.
+ Đường kính của gương là: \(2OA\).
Lời giải chi tiết:
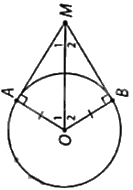
Gọi O là tâm của chiếc gương.
Vì MA, MB là tiếp tuyến của (O) nên:
+ MO là tia phân giác góc AMB, suy ra:
\(\widehat {AMO} = \widehat {BMO} = \frac{1}{2}\widehat {AMB} = \frac{1}{2}{.52^o} = {26^o}\).
+ \(MA = MB = \frac{{82}}{2} = 41cm\).
Vì MA là tiếp tuyến của (O) nên \(MA \bot AO\). Do đó, tam giác AMO vuông tại A.
Suy ra: \(OA = AM.\tan AMO = 41.\tan {26^o}\).
Vậy đường kính của gương là: \(2OA = 2.41.\tan {26^o} \approx 40\left( {cm} \right)\)
Mục 2 của chương trình Toán 9 tập 1 thường tập trung vào các chủ đề như hàm số bậc nhất, đồ thị hàm số, và ứng dụng của hàm số trong giải quyết các bài toán thực tế. Việc nắm vững kiến thức trong mục này là nền tảng quan trọng để học tốt các chương tiếp theo.
Trang 112 thường chứa các bài tập về việc xác định hàm số bậc nhất, tìm hệ số góc và tung độ gốc. Các bài tập này giúp học sinh rèn luyện kỹ năng phân tích và nhận biết các yếu tố cơ bản của hàm số.
Bài 1: Cho hàm số y = 2x + 3. Hãy xác định hệ số góc và tung độ gốc của hàm số.
Lời giải:
Trang 113 thường tập trung vào các bài tập về việc vẽ đồ thị hàm số bậc nhất. Học sinh cần nắm vững cách xác định các điểm thuộc đồ thị và nối chúng lại để tạo thành đường thẳng.
Bài 2: Vẽ đồ thị của hàm số y = -x + 1.
Lời giải:
Trang 114 thường chứa các bài tập ứng dụng hàm số bậc nhất vào giải quyết các bài toán thực tế, ví dụ như bài toán về quãng đường, thời gian, vận tốc. Các bài tập này đòi hỏi học sinh phải vận dụng kiến thức đã học để phân tích và giải quyết vấn đề.
Bài 3: Một ô tô đi từ A đến B với vận tốc 60km/h. Hãy viết công thức tính quãng đường đi được của ô tô theo thời gian.
Lời giải:
Gọi s là quãng đường đi được của ô tô (km), t là thời gian ô tô đi (giờ). Ta có công thức: s = 60t.
Để giải tốt các bài tập về hàm số bậc nhất, học sinh cần:
Khi giải bài tập về hàm số bậc nhất, học sinh cần chú ý:
Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh đã có thể tự tin giải các bài tập trong mục 2 trang 112, 113, 114 SGK Toán 9 tập 1. Chúc các em học tập tốt!
| Chủ đề | Nội dung chính |
|---|---|
| Hàm số bậc nhất | Định nghĩa, hệ số góc, tung độ gốc |
| Đồ thị hàm số | Cách vẽ, xác định điểm thuộc đồ thị |
| Ứng dụng | Giải bài toán thực tế |