Chào mừng các em học sinh đến với bài giải bài tập 9.5 trang 68 SGK Toán 9 tập 2 trên giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán. Đồng thời, chúng tôi cũng cung cấp các phương pháp giải khác nhau để các em có thể lựa chọn cách phù hợp nhất với bản thân.
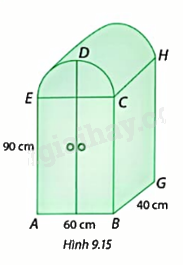
Hình 9.15 là một tủ chứa đồ. Biết cung CDE là nửa đường tròn. a) Tính thể tích của tủ đồ. b) Người ta muốn sơn tất cả các mặt ngoài của tủ (kể cả đáy). Hỏi diện tích cần sơn là bao nhiêu mét vuông (làm tròn kết quả đến hàng phần mười)?
Đề bài
Hình 9.15 là một tủ chứa đồ. Biết cung CDE là nửa đường tròn.
a) Tính thể tích của tủ đồ.
b) Người ta muốn sơn tất cả các mặt ngoài của tủ (kể cả đáy). Hỏi diện tích cần sơn là bao nhiêu mét vuông (làm tròn kết quả đến hàng phần mười)?
Phương pháp giải - Xem chi tiết
Dựa vào thể tích hình trụ: V = \(\pi {r^2}h\) (với r là bán kính đáy và h là chiều cao hình trụ).
Dựa vào: Diện tích xung quanh hình hộp chữ nhật Sxq = (a + b).2 (với a,b lần lượt là chiều dài, chiều rộng), diện tích xung quanh hình trụ \({S_{xq}} = 2\pi rh\) (với r là bán kính đáy và h là chiều cao hình trụ).
Lời giải chi tiết
a) Thể tích phần thân tủ dưới dạng hình hộp chữ nhật là 90.60.40 = 216000 (cm3)
Thể tích phần thân tủ trên là: \(\frac{{\pi {{.30}^2}.40}}{2} = 18000\pi \) (cm3)
Vậy thể tích của tủ đồ là: 216000 + \(18000\pi \) = 272548,7 (cm3).
b) Diện tích phần cần sơn bao gồm diện tích xung quanh của phần dạng hình hộp chữ nhật, diện tích mặt đáy, một nửa diện tích toàn phần của nửa hình trụ (diện tích phần thân tủ trên.
Diện tích cần sơn của phần thân tủ dưới dạng hình hộp chữ nhật là:
Sxq + Sđáy = (40 + 60).2.90 + 40.60 = 20400 (cm2)
Diện tích cần sơn của phần thân tủ trên (nửa hình trụ) là: \(\frac{{2\pi .30.40} + 2\pi.30^2}{2} = 2100\pi \) (cm2)
Vậy diện tích cần sơn là: 20400 + 2100\(\pi \) \( \approx \) 26997,3 cm2.
Bài tập 9.5 trang 68 SGK Toán 9 tập 2 yêu cầu chúng ta xét dấu của hàm số bậc nhất y = ax + b. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về hàm số bậc nhất, bao gồm:
Để giải bài tập này, chúng ta cần thực hiện các bước sau:
Giả sử chúng ta có hàm số y = 2x - 4. Hãy xét dấu của hàm số này.
| x | 2x - 4 |
|---|---|
| x < 2 | < 0 |
| x = 2 | = 0 |
| x > 2 | > 0 |
Vậy, hàm số y = 2x - 4 có giá trị âm khi x < 2, bằng 0 khi x = 2, và dương khi x > 2.
Khi xét dấu của hàm số, cần chú ý đến các trường hợp sau:
Để củng cố kiến thức, các em có thể tự giải các bài tập sau:
Việc nắm vững phương pháp xét dấu của hàm số bậc nhất là rất quan trọng để giải các bài tập liên quan đến hàm số và ứng dụng trong thực tế. Hy vọng bài giải chi tiết này sẽ giúp các em hiểu rõ hơn về bài tập 9.5 trang 68 SGK Toán 9 tập 2 và tự tin hơn trong quá trình học tập.