Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho mục 2 trang 76, 77 SGK Toán 9 tập 1. Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán và đạt kết quả tốt trong môn Toán.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn bài giải một cách cẩn thận, kèm theo các bước giải thích rõ ràng, giúp các em dễ dàng theo dõi và hiểu bài.
Trong Hình 4.6, tam giác ABC là tam giác gì? Xác định số đo và các tỉ số lượng giác của góc B.
Trả lời câu hỏi Luyện tập 2 trang 77 SGK Toán 9 Cùng khám phá
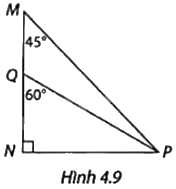
Trong Hình 4.9,hãy tính các tỉ số \(\frac{{PN}}{{PQ}}\) và \(\frac{{PN}}{{PM}}\), từ đó tìm \(\frac{{PQ}}{{PM}}\).
Phương pháp giải:
+ Xét tam giác NPQ vuông tại N có: \(\sin NQP = \frac{{PN}}{{PQ}}\), từ đó tính PQ theo PN và sin NQP.
+ Xét tam giác NPM vuông tại N có: \(\sin M = \frac{{NP}}{{MP}}\), từ đó tính MP theo PN và sinM.
+ Do đó, tính được tỉ số \(\frac{{PQ}}{{PM}}\)
Lời giải chi tiết:
Xét tam giác NPQ vuông tại N có:
\(\sin NQP = \frac{{PN}}{{PQ}}\) nên \(PQ = PN.\sin NQP = PN.\sin {60^o} = \frac{{\sqrt 3 }}{2}PN\).
Xét tam giác NPM vuông tại N có:
\(\sin M = \frac{{NP}}{{MP}}\), nên \(MP = PN.\sin M = PN.\sin {45^o} = \frac{{\sqrt 2 }}{2}PN\).
Do đó, \(\frac{{PQ}}{{PM}} = \frac{{\frac{{\sqrt 3 }}{2}PN}}{{\frac{{\sqrt 2 }}{2}PN}} = \frac{{\sqrt 6 }}{2}\)
Trả lời câu hỏi Hoạt động 2 trang 76 SGK Toán 9 Cùng khám phá
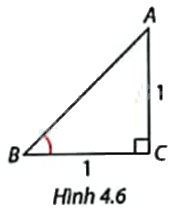
Trong Hình 4.6, tam giác ABC là tam giác gì? Xác định số đo và các tỉ số lượng giác của góc B.
Phương pháp giải:
Trong tam giác vuông có góc nhọn \(\alpha \), khi đó:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là \(\sin \alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là \(\cos \alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là \(\tan \alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là \(\cot \alpha \).
Lời giải chi tiết:
Tam giác ABC vuông tại C, \(CB = AC = 1\) nên tam giác ABC vuông cân tại C. Do đó, \(\widehat B = {45^o}\).
Tam giác ABC vuông tại C nên \(A{B^2} = B{C^2} + A{C^2} = {1^2} + {1^2} = 2\) (Định lí Pythagore).
Do đó, \(AB = \sqrt 2 \).
Suy ra, \(\sin B = \frac{{AC}}{{AB}} = \frac{1}{{\sqrt 2 }}\), \(\cos B = \frac{{BC}}{{AB}} = \frac{1}{{\sqrt 2 }}\), \(\tan B = \frac{{AC}}{{BC}} = 1\), \(\cot B = \frac{{BC}}{{AC}} = 1\).
Trả lời câu hỏi Hoạt động 3 trang 77SGK Toán 9 Cùng khám phá
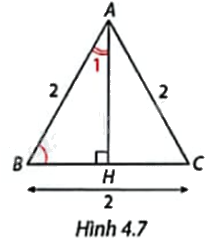
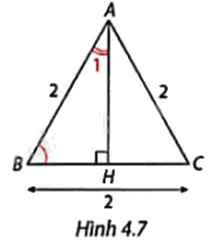
Trong Hình 4.7, tam giác ABC là tam giác gì? Xác định số đo và các tỉ số lượng giác của góc B và góc \({A_1}\).
Phương pháp giải:
Trong tam giác vuông có góc nhọn \(\alpha \), khi đó:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là \(\sin \alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là \(\cos \alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là \(\tan \alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là \(\cot \alpha \).
Lời giải chi tiết:
Tam giác ABC có \(AB = BC = CA = 2\) nên tam giác ABC đều.
Do đó, AH là đường cao đồng thời là đường trung tuyến.
Do đó, \(BH = \frac{1}{2}BC = \frac{1}{2}.2 = 1\).
Tam giác AHB vuông tại H nên \(A{H^2} + H{B^2} = A{B^2}\) (Định lí Pythagore).
Suy ra: \(A{H^2} = A{B^2} - B{H^2} = {2^2} - {1^2} = 3\).
Do đó, \(AH = \sqrt 3 \)
Do đó, \(\sin B = \frac{{AH}}{{AB}} = \frac{{\sqrt 3 }}{2}\), \(\cos B = \frac{{BH}}{{AB}} = \frac{1}{2}\), \(\tan B = \frac{{AH}}{{BH}} = \frac{{\sqrt 3 }}{1} = \sqrt 3 \), \(\cot B = \frac{{BH}}{{AH}} = \frac{1}{{\sqrt 3 }}\).
\(\sin {A_1} = \frac{{BH}}{{AB}} = \frac{1}{2}\), \(\cos {A_1} = \frac{{AH}}{{AB}} = \frac{{\sqrt 3 }}{2}\), \(\tan {A_1} = \frac{{BH}}{{AH}} = \frac{1}{{\sqrt 3 }}\), \(\cot {A_1} = \frac{{AH}}{{BH}} = \frac{{\sqrt 3 }}{1} = \sqrt 3 \).
Tam giác ABC đều nên \(\widehat B = {60^o}\).
Tam giác AHB vuông tại H nên \(\widehat {{A_1}} = {90^o} - \widehat B = {30^o}\).
Trả lời câu hỏi Hoạt động 2 trang 76 SGK Toán 9 Cùng khám phá
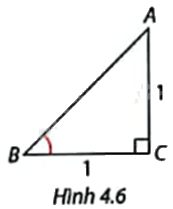
Trong Hình 4.6, tam giác ABC là tam giác gì? Xác định số đo và các tỉ số lượng giác của góc B.
Phương pháp giải:
Trong tam giác vuông có góc nhọn \(\alpha \), khi đó:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là \(\sin \alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là \(\cos \alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là \(\tan \alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là \(\cot \alpha \).
Lời giải chi tiết:
Tam giác ABC vuông tại C, \(CB = AC = 1\) nên tam giác ABC vuông cân tại C. Do đó, \(\widehat B = {45^o}\).
Tam giác ABC vuông tại C nên \(A{B^2} = B{C^2} + A{C^2} = {1^2} + {1^2} = 2\) (Định lí Pythagore).
Do đó, \(AB = \sqrt 2 \).
Suy ra, \(\sin B = \frac{{AC}}{{AB}} = \frac{1}{{\sqrt 2 }}\), \(\cos B = \frac{{BC}}{{AB}} = \frac{1}{{\sqrt 2 }}\), \(\tan B = \frac{{AC}}{{BC}} = 1\), \(\cot B = \frac{{BC}}{{AC}} = 1\).
Trả lời câu hỏi Hoạt động 3 trang 77SGK Toán 9 Cùng khám phá
Trong Hình 4.7, tam giác ABC là tam giác gì? Xác định số đo và các tỉ số lượng giác của góc B và góc \({A_1}\).
Phương pháp giải:
Trong tam giác vuông có góc nhọn \(\alpha \), khi đó:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là \(\sin \alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là \(\cos \alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là \(\tan \alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là \(\cot \alpha \).
Lời giải chi tiết:
Tam giác ABC có \(AB = BC = CA = 2\) nên tam giác ABC đều.
Do đó, AH là đường cao đồng thời là đường trung tuyến.
Do đó, \(BH = \frac{1}{2}BC = \frac{1}{2}.2 = 1\).
Tam giác AHB vuông tại H nên \(A{H^2} + H{B^2} = A{B^2}\) (Định lí Pythagore).
Suy ra: \(A{H^2} = A{B^2} - B{H^2} = {2^2} - {1^2} = 3\).
Do đó, \(AH = \sqrt 3 \)
Do đó, \(\sin B = \frac{{AH}}{{AB}} = \frac{{\sqrt 3 }}{2}\), \(\cos B = \frac{{BH}}{{AB}} = \frac{1}{2}\), \(\tan B = \frac{{AH}}{{BH}} = \frac{{\sqrt 3 }}{1} = \sqrt 3 \), \(\cot B = \frac{{BH}}{{AH}} = \frac{1}{{\sqrt 3 }}\).
\(\sin {A_1} = \frac{{BH}}{{AB}} = \frac{1}{2}\), \(\cos {A_1} = \frac{{AH}}{{AB}} = \frac{{\sqrt 3 }}{2}\), \(\tan {A_1} = \frac{{BH}}{{AH}} = \frac{1}{{\sqrt 3 }}\), \(\cot {A_1} = \frac{{AH}}{{BH}} = \frac{{\sqrt 3 }}{1} = \sqrt 3 \).
Tam giác ABC đều nên \(\widehat B = {60^o}\).
Tam giác AHB vuông tại H nên \(\widehat {{A_1}} = {90^o} - \widehat B = {30^o}\).
Trả lời câu hỏi Luyện tập 2 trang 77 SGK Toán 9 Cùng khám phá
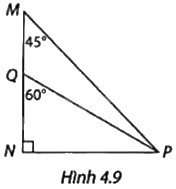
Trong Hình 4.9,hãy tính các tỉ số \(\frac{{PN}}{{PQ}}\) và \(\frac{{PN}}{{PM}}\), từ đó tìm \(\frac{{PQ}}{{PM}}\).
Phương pháp giải:
+ Xét tam giác NPQ vuông tại N có: \(\sin NQP = \frac{{PN}}{{PQ}}\), từ đó tính PQ theo PN và sin NQP.
+ Xét tam giác NPM vuông tại N có: \(\sin M = \frac{{NP}}{{MP}}\), từ đó tính MP theo PN và sinM.
+ Do đó, tính được tỉ số \(\frac{{PQ}}{{PM}}\)
Lời giải chi tiết:
Xét tam giác NPQ vuông tại N có:
\(\sin NQP = \frac{{PN}}{{PQ}}\) nên \(PQ = PN.\sin NQP = PN.\sin {60^o} = \frac{{\sqrt 3 }}{2}PN\).
Xét tam giác NPM vuông tại N có:
\(\sin M = \frac{{NP}}{{MP}}\), nên \(MP = PN.\sin M = PN.\sin {45^o} = \frac{{\sqrt 2 }}{2}PN\).
Do đó, \(\frac{{PQ}}{{PM}} = \frac{{\frac{{\sqrt 3 }}{2}PN}}{{\frac{{\sqrt 2 }}{2}PN}} = \frac{{\sqrt 6 }}{2}\)
Mục 2 trang 76, 77 SGK Toán 9 tập 1 thường xoay quanh các chủ đề về hàm số bậc nhất, bao gồm việc xác định hàm số, vẽ đồ thị hàm số, và ứng dụng của hàm số trong giải quyết các bài toán thực tế. Để giải tốt các bài tập trong mục này, học sinh cần nắm vững các khái niệm cơ bản về hàm số, đặc biệt là hàm số bậc nhất.
Hàm số bậc nhất có dạng y = ax + b, trong đó a và b là các số thực, a ≠ 0. 'a' được gọi là hệ số góc, quyết định độ dốc của đường thẳng biểu diễn hàm số. 'b' là tung độ gốc, là giao điểm của đường thẳng với trục Oy.
Để xác định một hàm số bậc nhất, ta cần biết hai điểm thuộc đồ thị hàm số hoặc biết hệ số góc 'a' và tung độ gốc 'b'. Ví dụ, nếu cho hai điểm A(x1, y1) và B(x2, y2) thuộc đồ thị hàm số, ta có thể tính hệ số góc 'a' bằng công thức: a = (y2 - y1) / (x2 - x1).
Để vẽ đồ thị hàm số y = ax + b, ta thực hiện các bước sau:
Lưu ý: Nếu a > 0, hàm số đồng biến (đồ thị đi lên). Nếu a < 0, hàm số nghịch biến (đồ thị đi xuống).
Hàm số bậc nhất có nhiều ứng dụng trong thực tế, ví dụ như:
Bài tập 1: Xác định hàm số bậc nhất đi qua hai điểm A(1, 2) và B(3, 6).
Lời giải: Hệ số góc a = (6 - 2) / (3 - 1) = 2. Thay điểm A(1, 2) vào phương trình y = 2x + b, ta có 2 = 2 * 1 + b => b = 0. Vậy hàm số bậc nhất cần tìm là y = 2x.
Bài tập 2: Vẽ đồ thị hàm số y = -x + 3.
Lời giải: Xác định hai điểm thuộc đồ thị hàm số. Ví dụ, khi x = 0, y = 3 (điểm A(0, 3)). Khi x = 3, y = 0 (điểm B(3, 0)). Vẽ đường thẳng đi qua hai điểm A và B.
Các bài tập về hàm số bậc nhất thường gặp các dạng sau:
Để giải các bài tập này, học sinh cần nắm vững các khái niệm cơ bản, các công thức và phương pháp giải đã được trình bày ở trên. Ngoài ra, việc luyện tập thường xuyên cũng rất quan trọng để củng cố kiến thức và rèn luyện kỹ năng giải bài tập.
Để học tốt môn Toán nói chung và hàm số bậc nhất nói riêng, các em nên:
Hy vọng với bài viết này, các em học sinh đã có thêm kiến thức và kỹ năng để giải quyết các bài tập về mục 2 trang 76, 77 SGK Toán 9 tập 1 một cách hiệu quả. Chúc các em học tập tốt!