Chào mừng bạn đến với bài học về Lý thuyết Bất phương trình bậc nhất một ẩn Toán 9 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp cho bạn kiến thức nền tảng, các quy tắc quan trọng và ví dụ minh họa để bạn có thể hiểu rõ và áp dụng thành thạo kiến thức này.
Bất phương trình bậc nhất một ẩn là một phần quan trọng trong chương trình Toán 9, giúp bạn rèn luyện tư duy logic và kỹ năng giải quyết vấn đề. Hãy cùng bắt đầu khám phá nhé!
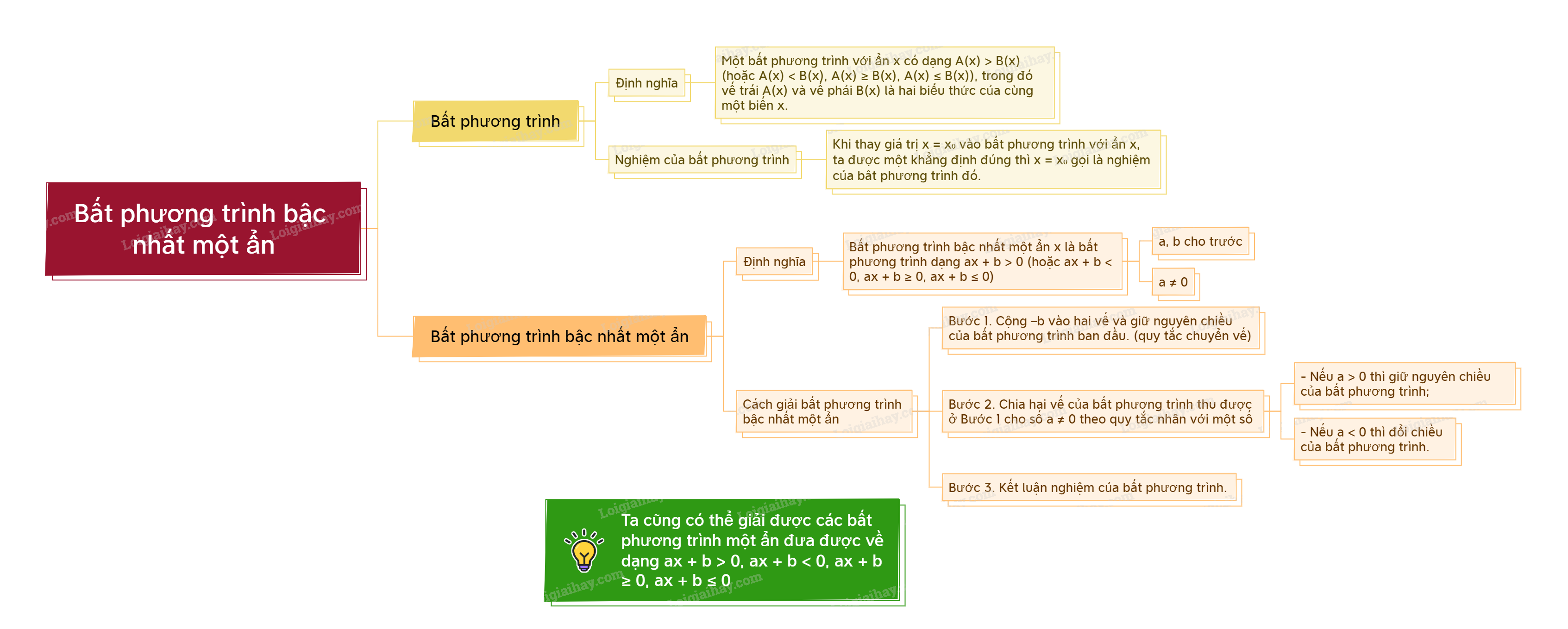
1. Mở đầu về bất phương trình Định nghĩa bất phương trình Cho A(x), B(x) là hai biểu thức của biến x. Khi cần tìm x sao cho A(x) > B(x) (hoặc A(x) < B(x), A(x) ( & ge ) B(x), A(x) ( le ) B(x)) thì ta nói cho A(x) > B(x) (hoặc A(x) < B(x), A(x) ( & ge ) B(x), A(x) ( le ) B(x)) là một bất phương trình ẩn x. A(x) và B(x) lần lượt được gọi là vế trái và vế phải của bất phương trình.
1. Mở đầu về bất phương trình
Định nghĩa bất phương trình
Cho A(x), B(x) là hai biểu thức của biến x. Khi cần tìm x sao cho A(x) > B(x) (hoặc A(x) < B(x), A(x) \( \ge \) B(x), A(x) \( \le \) B(x)) thì ta nói cho A(x) > B(x) (hoặc A(x) < B(x), A(x) \( \ge \) B(x), A(x) \( \le \) B(x)) là một bất phương trình ẩn x. A(x) và B(x) lần lượt được gọi là vế trái và vế phải của bất phương trình. |
Nghiệm của bất phương trình
Khi thay giá trị \(x = {x_0}\) vào hai vế của một bất phương trình ẩn x mà được một khẳng định đúng thì ta nói \(x = {x_0}\) (hay \({x_0}\)) là một nghiệm của bất phương trình đó. |
Ví dụ:
Số -2 là nghiệm của bất phương trình \(2x - 10 < 0\) vì \(2.\left( { - 2} \right) - 10 = - 4 - 10 = - 14 < 0\).
Số 6 không là nghiệm của bất phương trình \(2x - 10 < 0\) vì \(2.6 - 10 = 12 - 10 = 2 > 0\).
2. Bất phương trình bậc nhất một ẩn
Định nghĩa
Bất phương trình dạng \(ax + b > 0\) (hoặc \(ax + b < 0,ax + b \ge 0,ax + b \le 0\)), trong đó a, b là hai số đã cho, \(a \ne 0\) được gọi là bất phương trình bậc nhất một ẩn (x là ẩn). |
Ví dụ: \(3x + 16 \le 0\); \( - 3x > 0\) là các bất phương trình bậc nhất một ẩn x.
\({x^2} - 4 \ge 0\) không phải là một bất phương trình bậc nhất một ẩn x vì \({x^2} - 4\) là một đa thức bậc hai.
\(3x - 2y < 2\) không phải là một bất phương trình bậc nhất một ẩn vì đa thức \(3x - 2y\) là đa thức với hai biến x và y.
3. Cách giải bất phương trình bậc nhất một ẩn
Giải một bất phương trình nghĩa là tìm tất cả các nghiệm của nó.
Để giải bất phương trình \(ax + b > 0\) (hoặc \(ax + b < 0,ax + b \ge 0,ax + b \le 0\)), trong đó \(a \ne 0\), ta thực hiện ba bước sau: Bước 1. Cộng –b vào hai vế và giữ nguyên chiều của bất phương trình ban đầu. Bước 2. Chia hai vế của bất phương trình thu được ở Bước 1 cho số \(a \ne 0\) theo quy tắc: - Nếu \(a > 0\) thì giữ nguyên chiều của bất phương trình; - Nếu \(a < 0\) thì đổi chiều của bất phương trình. Bước 3. Kết luận nghiệm của bất phương trình. |
Ví dụ:Giải bất phương trình \( - 2x - 4 > 0\)
Lời giải:Ta có:
\(\begin{array}{l} - 2x - 4 > 0\\ - 2x > 0 + 4\\ - 2x > 4\\x < 4.\left( { - \frac{1}{2}} \right)\\x < - 2\end{array}\)
Vậy nghiệm của bất phương trình là \(x < - 2\).
Lưu ý:
Ở Bước 1, ta đã thực hiện quy tắc sau, gọi là quy tắc chuyển vế: Khi chuyển một hạng tử từ vế này sang vế kia, ta phải đổi dấu hạng tử đó.
Quy tắc thực hiện ở Bước 2 gọi là quy tắc nhân với một số: Khi nhân hai vế của một bất phương trình cùng một số khác 0, ta phải:
- Giữ nguyên chiều bất phương trình nếu số đó dương;
- Đổi chiều bất phương trình nếu số đó âm.
Nhờ hai quy tắc này, ta có thể giải được nhiều bất phương trình phức tạp hơn.
Bất phương trình bậc nhất một ẩn là một công cụ toán học mạnh mẽ, được sử dụng rộng rãi trong nhiều lĩnh vực của khoa học và kỹ thuật. Việc nắm vững lý thuyết và kỹ năng giải bất phương trình bậc nhất một ẩn là rất quan trọng đối với học sinh lớp 9, không chỉ để đạt kết quả tốt trong môn Toán mà còn để phát triển tư duy logic và khả năng giải quyết vấn đề.
Bất phương trình bậc nhất một ẩn là bất phương trình có dạng:
Trong đó:
Để giải bất phương trình bậc nhất một ẩn, chúng ta sử dụng các phép biến đổi tương đương. Hai bất phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm.
Các phép biến đổi tương đương thường được sử dụng:
Quy tắc chuyển vế là một trường hợp đặc biệt của phép cộng hoặc trừ cả hai vế của bất phương trình.
Ví dụ:
Để giải bất phương trình bậc nhất một ẩn, ta thực hiện các bước sau:
Ví dụ 1: Giải bất phương trình 2x + 3 > 7
Giải:
Vậy tập nghiệm của bất phương trình là x > 2.
Ví dụ 2: Giải bất phương trình -3x + 5 ≤ 11
Giải:
Vậy tập nghiệm của bất phương trình là x ≥ -2.
Để củng cố kiến thức, bạn hãy thử giải các bài tập sau:
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về Lý thuyết Bất phương trình bậc nhất một ẩn Toán 9. Chúc bạn học tập tốt!