Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho mục 2 trang 32, 33 SGK Toán 9 tập 2. Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán và đạt kết quả tốt trong môn Toán.
Trong Hình 7.6, O là giao điểm của ba đường phân giác của (Delta )ABC và OM, ON, OP là các đường vuông góc hạ từ O xuống ba cạnh của tam giác. Giải thích vì sao đường tròn tâm O bán kính OM tiếp xúc cả ba cạnh của (Delta )ABC.
Trả lời câu hỏi Luyện tập 2 trang 33 SGK Toán 9 Cùng khám phá
Tính bán kính đường tròn nội tiếp tam giác đều ABC có cạnh là \(2\sqrt 3 \)cm.
Phương pháp giải:
Đường tròn nội tiếp của tam giác đều cạnh a có tâm là trọng tâm tam giác đều và bán kính bằng \(\frac{{a\sqrt 3 }}{6}\).
Lời giải chi tiết:
Bán kính đường tròn nội tiếp tam giác đều ABC có cạnh là \(2\sqrt 3 \)cm là \(\frac{{2\sqrt 3 .\sqrt 3 }}{6} = 1\) cm.
Trả lời câu hỏi Hoạt động 2 trang 32 SGK Toán 9 Cùng khám phá
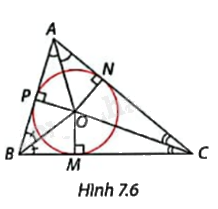
Trong Hình 7.6, O là giao điểm của ba đường phân giác của \(\Delta \)ABC và OM, ON, OP là các đường vuông góc hạ từ O xuống ba cạnh của tam giác. Giải thích vì sao đường tròn tâm O bán kính OM tiếp xúc cả ba cạnh của \(\Delta \)ABC.
Phương pháp giải:
Ba đường phân giác của một tam giác cùng đi qua một điểm và điểm này cách đều ba cạnh của tam giác.
Lời giải chi tiết:
Ta có ba đường phân giác của tam giác ABC cùng đi qua một điểm O nên ta có OP = ON = OM. Vì vậy đường tròn tâm O bán kính OM tiếp xúc cả ba cạnh của \(\Delta \)ABC.
Trả lời câu hỏi Vận dụng trang 33SGK Toán 9 Cùng khám phá
Tam giác đều ABC có cạnh bằng 6 cm. Tính tổng chu vi của \(\Delta \)ABC, chu vi đường tròn nội tiếp và chu vi đường tròn ngoại tiếp của nó. Từ đó trả lời câu hỏi của bài toán ở phần Khởi động.
Phần Khởi động: Bạn Uyên dùng một sợi thép để uốn thành mẫu hoạ tiết (Hình 7.1). Độ dài của sợi thép ít nhất là bao nhiêu để tam giác đều trong mẫu hoạ tiết có cạnh bằng 6 cm?

Phương pháp giải:
Chu vi tam giác đều P = 3a
Bán kính đường tròn nội tiếp của tam giác đều bằng \(\frac{{a\sqrt 3 }}{6}\).
Chu vi đường tròn nội tiếp của tam giác đều là S = \(2\pi r\)
Bán kính đường tròn ngoại tiếp của tam giác đều bằng \(\frac{{a\sqrt 3 }}{3}\).
Chu vi đường tròn ngoại tiếp của tam giác đều là S = \(2\pi R\)
Lời giải chi tiết:
Chu vi tam giác đều P = 3a = 3.6 = 18 cm.
Bán kính đường tròn nội tiếp của tam giác đều bằng \(\frac{{a\sqrt 3 }}{6} = \frac{{6\sqrt 3 }}{6} = \sqrt 3 \)cm.
Chu vi đường tròn nội tiếp của tam giác đều là S = \(2\pi r = 2\sqrt 3 \pi \).
Bán kính đường tròn ngoại tiếp của tam giác đều bằng \(\frac{{a\sqrt 3 }}{3} = \frac{{6\sqrt 3 }}{3} = 2\sqrt 3 \)cm.
Chu vi đường tròn ngoại tiếp của tam giác đều là S = \(2\pi R = 4\sqrt 3 \pi \)cm.
Vậy độ dài của sợi thép ít nhất là: \(18 + 2\sqrt 3 \pi + 4\sqrt 3 \pi \approx 50,65\)cm.
Trả lời câu hỏi Hoạt động 2 trang 32 SGK Toán 9 Cùng khám phá
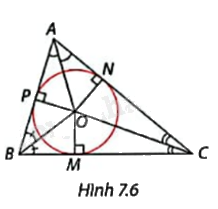
Trong Hình 7.6, O là giao điểm của ba đường phân giác của \(\Delta \)ABC và OM, ON, OP là các đường vuông góc hạ từ O xuống ba cạnh của tam giác. Giải thích vì sao đường tròn tâm O bán kính OM tiếp xúc cả ba cạnh của \(\Delta \)ABC.
Phương pháp giải:
Ba đường phân giác của một tam giác cùng đi qua một điểm và điểm này cách đều ba cạnh của tam giác.
Lời giải chi tiết:
Ta có ba đường phân giác của tam giác ABC cùng đi qua một điểm O nên ta có OP = ON = OM. Vì vậy đường tròn tâm O bán kính OM tiếp xúc cả ba cạnh của \(\Delta \)ABC.
Trả lời câu hỏi Luyện tập 2 trang 33 SGK Toán 9 Cùng khám phá
Tính bán kính đường tròn nội tiếp tam giác đều ABC có cạnh là \(2\sqrt 3 \)cm.
Phương pháp giải:
Đường tròn nội tiếp của tam giác đều cạnh a có tâm là trọng tâm tam giác đều và bán kính bằng \(\frac{{a\sqrt 3 }}{6}\).
Lời giải chi tiết:
Bán kính đường tròn nội tiếp tam giác đều ABC có cạnh là \(2\sqrt 3 \)cm là \(\frac{{2\sqrt 3 .\sqrt 3 }}{6} = 1\) cm.
Trả lời câu hỏi Vận dụng trang 33SGK Toán 9 Cùng khám phá
Tam giác đều ABC có cạnh bằng 6 cm. Tính tổng chu vi của \(\Delta \)ABC, chu vi đường tròn nội tiếp và chu vi đường tròn ngoại tiếp của nó. Từ đó trả lời câu hỏi của bài toán ở phần Khởi động.
Phần Khởi động: Bạn Uyên dùng một sợi thép để uốn thành mẫu hoạ tiết (Hình 7.1). Độ dài của sợi thép ít nhất là bao nhiêu để tam giác đều trong mẫu hoạ tiết có cạnh bằng 6 cm?

Phương pháp giải:
Chu vi tam giác đều P = 3a
Bán kính đường tròn nội tiếp của tam giác đều bằng \(\frac{{a\sqrt 3 }}{6}\).
Chu vi đường tròn nội tiếp của tam giác đều là S = \(2\pi r\)
Bán kính đường tròn ngoại tiếp của tam giác đều bằng \(\frac{{a\sqrt 3 }}{3}\).
Chu vi đường tròn ngoại tiếp của tam giác đều là S = \(2\pi R\)
Lời giải chi tiết:
Chu vi tam giác đều P = 3a = 3.6 = 18 cm.
Bán kính đường tròn nội tiếp của tam giác đều bằng \(\frac{{a\sqrt 3 }}{6} = \frac{{6\sqrt 3 }}{6} = \sqrt 3 \)cm.
Chu vi đường tròn nội tiếp của tam giác đều là S = \(2\pi r = 2\sqrt 3 \pi \).
Bán kính đường tròn ngoại tiếp của tam giác đều bằng \(\frac{{a\sqrt 3 }}{3} = \frac{{6\sqrt 3 }}{3} = 2\sqrt 3 \)cm.
Chu vi đường tròn ngoại tiếp của tam giác đều là S = \(2\pi R = 4\sqrt 3 \pi \)cm.
Vậy độ dài của sợi thép ít nhất là: \(18 + 2\sqrt 3 \pi + 4\sqrt 3 \pi \approx 50,65\)cm.
Mục 2 của SGK Toán 9 tập 2 thường tập trung vào một chủ đề cụ thể trong hình học hoặc đại số. Để giải quyết các bài tập trong mục này, học sinh cần nắm vững các định nghĩa, tính chất và định lý liên quan. Việc hiểu rõ lý thuyết là nền tảng để áp dụng vào giải bài tập một cách hiệu quả.
Bài tập 1 thường là bài tập áp dụng trực tiếp các kiến thức đã học. Để giải bài này, các em cần:
Bài tập 2 có thể là bài tập nâng cao hơn, đòi hỏi học sinh phải vận dụng kiến thức một cách linh hoạt và sáng tạo. Các em có thể tham khảo các ví dụ tương tự trong sách giáo khoa hoặc trên internet để tìm kiếm hướng giải quyết.
Bài tập 3 thường là bài tập tổng hợp, kết hợp nhiều kiến thức khác nhau. Để giải bài này, các em cần có cái nhìn tổng quan về chủ đề và khả năng liên kết các kiến thức lại với nhau.
Bài tập 4 có thể là bài tập thực tế, yêu cầu học sinh áp dụng kiến thức vào giải quyết các vấn đề trong cuộc sống. Các em cần phân tích tình huống thực tế và tìm ra cách giải quyết phù hợp.
Giả sử bài tập yêu cầu tính độ dài cạnh huyền của một tam giác vuông có hai cạnh góc vuông lần lượt là 3cm và 4cm. Các em có thể sử dụng định lý Pitago để giải bài toán này:
Độ dài cạnh huyền = √(32 + 42) = √(9 + 16) = √25 = 5cm
Việc giải bài tập Toán 9 tập 2 đòi hỏi sự kiên trì, cẩn thận và nắm vững kiến thức. Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em sẽ tự tin giải quyết các bài tập trong mục 2 trang 32, 33 SGK Toán 9 tập 2 một cách hiệu quả. Chúc các em học tốt!
| Công thức | Mô tả |
|---|---|
| Định lý Pitago | a2 + b2 = c2 (trong đó a, b là độ dài hai cạnh góc vuông, c là độ dài cạnh huyền) |
| Diện tích tam giác | S = (1/2) * đáy * chiều cao |