Chào mừng các em học sinh đến với bài giải bài tập 8.10 trang 55 SGK Toán 9 tập 2 trên giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
Tính số đo mỗi góc của khung gỗ trang trí có hình bát giác đều như Hình 8.37.
Đề bài
Tính số đo mỗi góc của khung gỗ trang trí có hình bát giác đều như Hình 8.37.
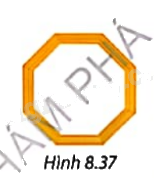
Phương pháp giải - Xem chi tiết
Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
Lời giải chi tiết
Hình bát giác đều có 8 góc bằng nhau nên số đo mỗi góc là: \(\frac{{{{360}^o}}}{8} = {45^o}\).
Bài tập 8.10 trang 55 SGK Toán 9 tập 2 yêu cầu chúng ta xét hàm số y = (m-1)x + 3. Để hàm số này là hàm số bậc nhất, điều kiện cần và đủ là hệ số m-1 khác 0. Bài viết này sẽ đi sâu vào phân tích điều kiện này và cách xác định giá trị của m để đảm bảo hàm số thỏa mãn yêu cầu.
Hàm số y = ax + b được gọi là hàm số bậc nhất khi và chỉ khi a khác 0. Trong trường hợp bài tập này, a = m-1. Do đó, để y = (m-1)x + 3 là hàm số bậc nhất, chúng ta cần có:
Điều này có nghĩa là giá trị của m không thể bằng 1. Nếu m = 1, hàm số sẽ trở thành y = 0x + 3 = 3, là một hàm số hằng, không phải hàm số bậc nhất.
Việc xác định m ≠ 1 là bước quan trọng để đảm bảo tính chất bậc nhất của hàm số. Khi m khác 1, hệ số góc của đường thẳng (m-1) sẽ khác 0, cho phép đường thẳng có độ dốc và cắt trục hoành tại một điểm xác định. Điều này tạo nên một đường thẳng thực sự, chứ không phải một đường thẳng trùng với trục tung hoặc là một đường thẳng nằm ngang.
Hãy xét một vài trường hợp cụ thể để hiểu rõ hơn:
Hàm số bậc nhất có nhiều ứng dụng trong thực tế, từ việc mô tả các mối quan hệ tuyến tính đến việc dự đoán xu hướng. Việc hiểu rõ các tính chất của hàm số bậc nhất, bao gồm hệ số góc, giao điểm với các trục tọa độ, và điều kiện để hàm số là bậc nhất, là nền tảng quan trọng cho việc học tập các chủ đề toán học nâng cao hơn.
Để củng cố kiến thức về hàm số bậc nhất, các em có thể luyện tập thêm các bài tập tương tự. Ví dụ:
Bài tập 8.10 trang 55 SGK Toán 9 tập 2 là một bài tập cơ bản nhưng quan trọng để hiểu rõ về hàm số bậc nhất. Việc nắm vững điều kiện để một hàm số là hàm số bậc nhất sẽ giúp các em giải quyết các bài tập phức tạp hơn một cách dễ dàng và hiệu quả. Hãy luyện tập thường xuyên và đừng ngần ngại tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè nếu gặp khó khăn.
Giaitoan.edu.vn hy vọng rằng bài giải chi tiết này sẽ giúp các em hiểu rõ hơn về bài tập 8.10 trang 55 SGK Toán 9 tập 2 và tự tin hơn trong việc học tập môn Toán.