Chào mừng bạn đến với bài học về Lý thuyết Tần số Toán 9 tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về tần số, giúp bạn hiểu rõ hơn về khái niệm này và ứng dụng nó vào giải các bài toán thực tế.
Chúng tôi sẽ cùng nhau khám phá định nghĩa, các loại tần số, cách tính tần số và những bài tập minh họa để bạn có thể nắm vững kiến thức một cách dễ dàng.
1. Tần số và bảng tần số Tập hợp các dữ liệu thu thập được khi điều tra thống kê về một dấu hiệu nào đó được gọi là mẫu dữ liệu. Số giá trị (có thể lặp lại) của mẫu dữ liệu được gọi là kích thước mẫu (hay cỡ mẫu).
1. Tần số và bảng tần số
Tập hợp các dữ liệu thu thập được khi điều tra thống kê về một dấu hiệu nào đó được gọi là mẫu dữ liệu. Số giá trị (có thể lặp lại) của mẫu dữ liệu được gọi là kích thước mẫu (hay cỡ mẫu).
Tần số
Số lần xuất hiện một giá trị trong mẫu dữ liệu có dấu hiệu điều tra được gọi là tần số của giá trị đó. |
Bảng tần số
Bảng tần số là bảng biểu diễn dữ liệu, trong đó: - Dòng (cột) thứ nhất ghi các giá trị khác nhau của dấu hiệu điều tra; - Dòng (cột) thứ hai ghi tần số của giá trị tương ứng ở dòng (cột) thứ nhất. |
Nhận xét: Trong bảng tần số với dữ liệu là số, người ta thường sắp xếp các giá trị từ nhỏ đến lớn (hoặc từ lớn đến nhỏ) và viết thêm tổng các tần số (tổng đó chính là kích thước mẫu).
Ví dụ: Thống kê khối lượng rau thu hoạch một vụ (đơn vị: tạ) của mỗi hộ gia đình trong 38 hộ gia đình tham gia chương trình trồng rau theo tiêu chuẩn VIETGAP như sau:

Trong 38 số liệu thống kê ở trên có 7 giá trị khác nhau là:
\({x_1} = 4;{x_2} = 5;{x_3} = 6;{x_4} = 7;{x_5} = 8;{x_6} = 9;{x_7} = 10\)
Tần số của giá trị \({x_1},{x_2},{x_3},{x_4},{x_5},{x_6},{x_7}\) lần lượt là:
\({m_1} = 4;{m_2} = 7;{m_3} = 5;{m_4} = 8;{m_5} = 7;{m_6} = 5;{m_7} = 2\).
Bảng tần số của mẫu số liệu thống kê là:

Nhận xét: Ý nghĩa và vai trò của tần số
Tần số cho ta biết mỗi giá trị xuất hiện nhiều hay ít trong mẫu. Bảng tần số biểu diễn dữ liệu gọn gàng và thuận tiện cho việc so sánh, xác định những giá trị phổ biến hoặc rất ít xuất hiện để từ đó ta có thể đưa ra kết luận hợp lí.
2. Biểu đồ tần số
Khái niệm
Bảng tần số có thể được biểu thị bởi biểu đồ cột hoặc biểu đồ đoạn thẳng. Các biểu đồ này được gọi là biểu đồ tần số dạng cột và biểu đồ tần số dạng đoạn thẳng. |
Ví dụ: Biểu đồ tần số của mẫu số thống kê trong bảng tần số sau:
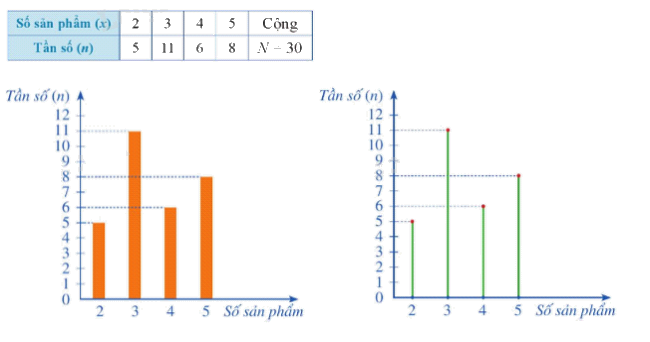
Nhận xét: Ý nghĩa và vai trò của biểu đồ tần số
- Biểu đồ tần số dạng cột biểu diễn một cách trực quan sự phân bố của dữ liệu. Nó cho ta biết dữ liệu tập trung nhiều nhất ở giá trị nào, ít xuất hiện nhất ở giá trị nào. Nó thuận tiện cho việc so sánh tần số của các giá trị hoặc xác định những giá trị đặc biệt trong mẫu dữ liệu.
- Biểu đồ tần số dạng đoạn thẳng biểu thị rõ xu hướng thay đổi tần số các giá trị theo thời gian, giúp ta so sánh mức độ biến động của tần số.
Lưu ý:
Khi biểu diễn bảng tần số bằng một biểu đồ hay khi đọc và phân tích dữ liệu trên các biểu đồ, ta phải chú ý đến đơn vị của trục tung, tránh đưa ra những kết luận không chính xác do chỉ căn cứ vào hình vẽ.
Lưu ý:
Khi vẽ biểu đồ, ta nên chọn đơn vị phù hợp cho trục tần số để có thể bắt đầu từ số 0, không gây nhầm lẫn về thị giác.
Ví dụ: Hai biểu đồ này cùng mô tả một dữ liệu.
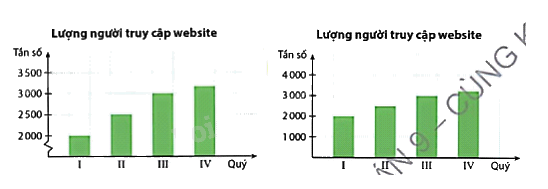
Trong toán học, đặc biệt là trong thống kê và xác suất, tần số đóng vai trò quan trọng trong việc mô tả sự xuất hiện của một giá trị hoặc một sự kiện trong một tập dữ liệu. Đối với học sinh lớp 9, việc hiểu rõ khái niệm tần số là nền tảng để tiếp cận các bài toán liên quan đến thống kê, biểu đồ và phân tích dữ liệu.
Định nghĩa: Tần số của một giá trị trong một tập dữ liệu là số lần giá trị đó xuất hiện trong tập dữ liệu đó.
Có một số loại tần số thường gặp trong toán học:
Việc tính tần số khá đơn giản. Bạn chỉ cần đếm số lần xuất hiện của một giá trị trong tập dữ liệu. Ví dụ:
Cho tập dữ liệu: 2, 3, 3, 4, 5, 5, 5, 6
Tổng số phần tử trong tập dữ liệu là 8.
Lý thuyết tần số có nhiều ứng dụng trong thực tế, bao gồm:
Một lớp học có 30 học sinh. Kết quả kiểm tra môn Toán của các học sinh được cho như sau:
| Điểm | Số học sinh |
|---|---|
| 5 | 3 |
| 6 | 5 |
| 7 | 8 |
| 8 | 7 |
| 9 | 4 |
| 10 | 3 |
Hãy tính tần số tương đối của mỗi điểm:
Để củng cố kiến thức về lý thuyết tần số, bạn hãy thử giải các bài tập sau:
Hy vọng bài học về Lý thuyết Tần số Toán 9 này đã giúp bạn hiểu rõ hơn về khái niệm tần số và ứng dụng của nó. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải các bài toán liên quan.