Chào mừng các em học sinh đến với bài giải bài tập 4.5 trang 82 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương Hàm số bậc nhất và là một phần quan trọng trong việc củng cố kiến thức về hàm số.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin làm bài tập.
Sử dụng máy tính cầm tay, tính số đo góc nhọn \(\alpha \), biết: a) \(\sin \alpha = 0,3\); b) \(\cos \alpha = \frac{1}{2}\); c) \(\tan \alpha = \frac{5}{7}\); d) \(\cot \alpha = 4\). Làm tròn số đo góc đến phút.
Đề bài
Sử dụng máy tính cầm tay, tính số đo góc nhọn \(\alpha \), biết:
a) \(\sin \alpha = 0,3\);
b) \(\cos \alpha = \frac{1}{2}\);
c) \(\tan \alpha = \frac{5}{7}\);
d) \(\cot \alpha = 4\).
Làm tròn số đo góc đến phút.
Phương pháp giải - Xem chi tiết
Sử dụng máy tính cầm tay để tính.
Lời giải chi tiết
a) Để tìm góc \(\alpha \) có \(\sin \alpha = 0,3\), ta lần lượt bấm các nút
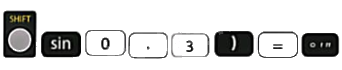
và được kết quả

Vậy \(\alpha \approx {17^o}27'\).
b) Để tìm góc \(\alpha \) có \(\cos \alpha = \frac{1}{2}\), ta lần lượt bấm các nút

ta được kết quả:

Vậy \(\alpha = {60^o}\).
c) Để tìm góc \(\alpha \) có \(\tan \alpha = \frac{5}{7}\), ta lần lượt bấm các nút

và được kết quả

Vậy \(\alpha \approx {35^o}32'\).
d) Để tìm góc \(\alpha \) có \(\cot \alpha = 4\), ta lần lượt bấm các nút

và được kết quả

Vậy \(\alpha \approx {14^o}2'\).
Bài tập 4.5 trang 82 SGK Toán 9 tập 1 yêu cầu chúng ta xét dấu của hàm số bậc nhất. Để giải bài tập này, trước hết cần nắm vững kiến thức về hàm số bậc nhất, đặc biệt là hệ số a và cách xác định khoảng đồng biến, nghịch biến của hàm số.
Bài tập thường yêu cầu xét dấu của một hàm số bậc nhất cụ thể. Ví dụ, xét hàm số y = 2x - 4. Để xét dấu, ta tìm nghiệm của phương trình 2x - 4 = 0, tức là x = 2. Sau đó, ta xét các khoảng:
Vậy, hàm số y = 2x - 4 âm khi x < 2, bằng 0 khi x = 2 và dương khi x > 2.
Do bài tập 4.5 có thể có nhiều dạng khác nhau, chúng ta sẽ xét một số ví dụ cụ thể:
Để hiểu rõ hơn về cách xét dấu hàm số bậc nhất, các em có thể làm thêm các bài tập tương tự trong SGK và sách bài tập. Hãy chú ý đến hệ số a và nghiệm của phương trình ax + b = 0 để xác định khoảng đồng biến, nghịch biến và xét dấu của hàm số.
Ngoài ra, các em có thể tham khảo thêm các tài liệu học toán online trên giaitoan.edu.vn để nâng cao kiến thức và kỹ năng giải bài tập.
Hy vọng với bài giải chi tiết này, các em sẽ hiểu rõ hơn về cách giải bài tập 4.5 trang 82 SGK Toán 9 tập 1. Chúc các em học tập tốt!