Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 1 trang 30, 31, 32 của sách giáo khoa Toán 9 tập 2.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, nắm vững phương pháp giải và tự tin làm bài tập.
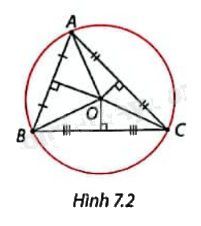
Vẽ tam giác ABC. Vẽ ba đường trung trực của tam giác ABC và xác định giao điểm O của chúng. Giải thích vì sao đường tròn tâm O bán kính OA đi qua cả ba đỉnh của (Delta )ABC. (Hình 7.2)
Trả lời câu hỏi Hoạt động 1 trang 30 SGK Toán 9 Cùng khám phá
Vẽ tam giác ABC. Vẽ ba đường trung trực của tam giác ABC và xác định giao điểm O của chúng. Giải thích vì sao đường tròn tâm O bán kính OA đi qua cả ba đỉnh của \(\Delta \)ABC. (Hình 7.2)
Phương pháp giải:
Ba đường trung trực của một tam giác cùng đi qua một điểm và điểm này cách đều ba đỉnh của tam giác.
Lời giải chi tiết:
Ta có ba đường trung trực của tam giác ABC cùng đi qua một điểm O nên ta có OC = OB = OA. Vì vậy đường tròn tâm O bán kính OA đi qua cả ba đỉnh của \(\Delta \)ABC.
Trả lời câu hỏi Luyện tập 1 trang 32SGK Toán 9 Cùng khám phá
Tam giác đều ABC có cạnh bằng 4, M là trung điểm của BC và O là trọng tâm. Xác định tâm, bán kính và vẽ đường tròn ngoại tiếp tam giác ABC và AMC.
Phương pháp giải:
Đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm của tam đều có bán kính bằng \(\frac{{a\sqrt 3 }}{3}\).
Lời giải chi tiết:
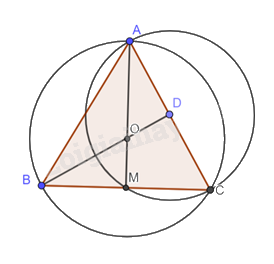
Đường tròn ngoại tiếp tam giác ABC có tâm là O, bán kính OA = \(\frac{{4\sqrt 3 }}{3}\) cm.
Đường tròn ngoại tiếp tam giác AMC có tâm là trung điểm AC là D, bán kính DA.
Ta có DA = \(\frac{1}{2}AC = \frac{1}{2}.4 = 2\) cm.
Trả lời câu hỏi Hoạt động 1 trang 30 SGK Toán 9 Cùng khám phá
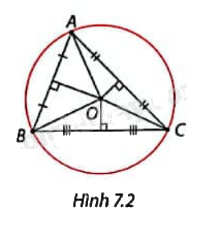
Vẽ tam giác ABC. Vẽ ba đường trung trực của tam giác ABC và xác định giao điểm O của chúng. Giải thích vì sao đường tròn tâm O bán kính OA đi qua cả ba đỉnh của \(\Delta \)ABC. (Hình 7.2)
Phương pháp giải:
Ba đường trung trực của một tam giác cùng đi qua một điểm và điểm này cách đều ba đỉnh của tam giác.
Lời giải chi tiết:
Ta có ba đường trung trực của tam giác ABC cùng đi qua một điểm O nên ta có OC = OB = OA. Vì vậy đường tròn tâm O bán kính OA đi qua cả ba đỉnh của \(\Delta \)ABC.
Trả lời câu hỏi Luyện tập 1 trang 32SGK Toán 9 Cùng khám phá
Tam giác đều ABC có cạnh bằng 4, M là trung điểm của BC và O là trọng tâm. Xác định tâm, bán kính và vẽ đường tròn ngoại tiếp tam giác ABC và AMC.
Phương pháp giải:
Đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm của tam đều có bán kính bằng \(\frac{{a\sqrt 3 }}{3}\).
Lời giải chi tiết:
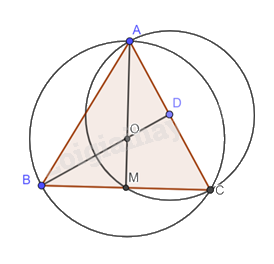
Đường tròn ngoại tiếp tam giác ABC có tâm là O, bán kính OA = \(\frac{{4\sqrt 3 }}{3}\) cm.
Đường tròn ngoại tiếp tam giác AMC có tâm là trung điểm AC là D, bán kính DA.
Ta có DA = \(\frac{1}{2}AC = \frac{1}{2}.4 = 2\) cm.
Mục 1 của SGK Toán 9 tập 2 thường tập trung vào một chủ đề quan trọng trong chương trình học. Việc nắm vững kiến thức và kỹ năng trong mục này là nền tảng để giải quyết các bài toán phức tạp hơn ở các chương tiếp theo. Chúng ta sẽ đi sâu vào từng bài tập, phân tích đề bài, trình bày lời giải chi tiết và cung cấp các lưu ý quan trọng.
Bài tập này yêu cầu học sinh vận dụng các công thức và phương pháp đã học để giải các phương trình bậc hai. Các phương pháp thường được sử dụng bao gồm:
Ví dụ: Giải phương trình x^2 - 5x + 6 = 0
Ta có thể phân tích thành nhân tử: (x - 2)(x - 3) = 0
Suy ra x = 2 hoặc x = 3
Bài tập này đòi hỏi học sinh phải chuyển đổi bài toán thực tế thành phương trình bậc hai và giải phương trình đó. Đây là một kỹ năng quan trọng giúp học sinh áp dụng kiến thức toán học vào cuộc sống.
Ví dụ: Một khu vườn hình chữ nhật có chiều dài hơn chiều rộng 5m. Diện tích khu vườn là 150m^2. Tính chiều dài và chiều rộng của khu vườn.
Gọi chiều rộng của khu vườn là x (m). Khi đó, chiều dài của khu vườn là x + 5 (m).
Diện tích khu vườn là x(x + 5) = 150
Suy ra x^2 + 5x - 150 = 0
Giải phương trình này, ta được x = 10 (chỉ nhận nghiệm dương).
Vậy chiều rộng của khu vườn là 10m và chiều dài là 15m.
Bài tập này yêu cầu học sinh phải hiểu rõ mối quan hệ giữa nghiệm và hệ số của phương trình bậc hai. Các công thức liên quan bao gồm:
Ví dụ: Cho phương trình x^2 - 3x + 2 = 0. Tính tổng và tích của hai nghiệm.
Ta có a = 1, b = -3, c = 2
Tổng hai nghiệm là x1 + x2 = -(-3)/1 = 3
Tích hai nghiệm là x1 * x2 = 2/1 = 2
Hy vọng với hướng dẫn chi tiết này, các em học sinh đã có thể tự tin giải các bài tập trong mục 1 trang 30, 31, 32 SGK Toán 9 tập 2. Hãy tiếp tục luyện tập và khám phá thêm nhiều kiến thức thú vị khác trên giaitoan.edu.vn!