Chào mừng các em học sinh đến với bài giải chi tiết mục 2 trang 71, 72 SGK Toán 9 tập 2 trên giaitoan.edu.vn. Chúng tôi cung cấp lời giải đầy đủ, chính xác, giúp các em hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Mục tiêu của chúng tôi là hỗ trợ các em học tập Toán 9 một cách hiệu quả nhất, đồng thời giúp các em tự tin hơn trong quá trình ôn tập và làm bài kiểm tra.
Cắt mặt xung quanh của một hình nón có đường sinh dài 6 cm, bán kính đáy 2 cm (Hình 9.22a) dọc theo đường sinh SA của nó rồi trải phẳng ra, ta được hình khai triển của hình nón đó (Hình 9.22b). a) Tính chu vi đáy của hình nón, từ đó cho biết độ dài cung ứng với hình quạt tròn ở Hình 9.22b. b) Tính diện tích của hình quạt tròn khai triển trong Hình 9.22b.
Trả lời câu hỏi Vận dụng 2 trang 72 SGK Toán 9 Cùng khám phá
Nón lá phổ biến ở cả ba miền của nước ta nhưng nón lá Huế từ lâu đã trở thành nguồn cảm hứng cho thi ca. Nón Huế thường có màu trắng xanh, thanh tao, mỏng, nhẹ, mềm mại. Nón lá Huế có khung gồm 16 vòng cách đều nhau (khuôn nón còn được gọi là khung chằm) và được lợp bằng nhiều lớp lá của cây lá nón trồng ở huyện A Lưới và huyện Nam Đông, thuộc tỉnh Thừa Thiên Huế. Tính diện tích bề mặt ngoài (theo centimet vuông) của một chiếc nón lá có đường kính đáy 41 cm và chiều cao 18 cm (làm tròn kết quả đến hàng phần mười).
Phương pháp giải:
Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rn\) (với r là bán kính đáy và n là đường sinh của hình nón).
Lời giải chi tiết:
Ta có đường sinh của chiếc nón lá là:
\(\sqrt {{{\left( {\frac{{41}}{2}} \right)}^2} + {{18}^2}} \approx 27,3\) cm (theo định lí pythagore)
Vậy diện tích bề mặt ngoài của chiếc nón lá là:
\({S_{xq}} = \pi rn = \pi .\frac{{41}}{2}.27,3 \approx 1758,2\)cm2
Trả lời câu hỏi Luyện tập 2 trang 72SGK Toán 9 Cùng khám phá
Tính chiều cao của một hình nó có đường sinh dài 20 cm và diện tích xung quanh bằng 240\(\pi \)cm2.
Phương pháp giải:
Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rn\) (với r là bán kính đáy và n là đường sinh của hình nón).
Lời giải chi tiết:
Ta có:\({S_{xq}} = \pi rn\)
suy ra r = \(\frac{{{S_{xq}}}}{{\pi .n}} = \frac{{240\pi }}{{\pi .20}} = 12\)cm.
Từ đó, ta có chiều cao của hình nón là:
\(\sqrt {{{20}^2} - {{12}^2}} = 16\) cm (Theo định lý Pythagore).
Trả lời câu hỏi Hoạt động 2 trang 71 SGK Toán 9 Cùng khám phá
Cắt mặt xung quanh của một hình nón có đường sinh dài 6 cm, bán kính đáy 2 cm (Hình 9.22a) dọc theo đường sinh SA của nó rồi trải phẳng ra, ta được hình khai triển của hình nón đó (Hình 9.22b).
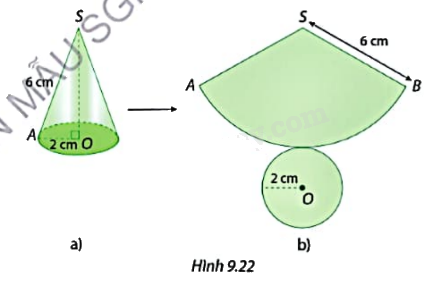
a) Tính chu vi đáy của hình nón, từ đó cho biết độ dài cung ứng với hình quạt tròn ở Hình 9.22b.
b) Tính diện tích của hình quạt tròn khai triển trong Hình 9.22b.
Phương pháp giải:
Chu vi đường tròn: C = \(\pi {r^2}\)(r là bán kính đường tròn).
Lời giải chi tiết:
a) Chu vi đáy hình nón là:
\(\pi {r^2} = 4\pi \)(cm).
Suy ra độ dài cung ứng với hình quạt tròn là: \(r.n\) (n: số đo góc ở tâm chắn cung đó).
b) Diện tích hình quạt tròn khai triển là:
S = \(\frac{{\pi .{r^2}.n}}{{360}}\).
Trả lời câu hỏi Luyện tập 2 trang 72SGK Toán 9 Cùng khám phá
Tính chiều cao của một hình nó có đường sinh dài 20 cm và diện tích xung quanh bằng 240\(\pi \)cm2.
Phương pháp giải:
Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rn\) (với r là bán kính đáy và n là đường sinh của hình nón).
Lời giải chi tiết:
Ta có:\({S_{xq}} = \pi rn\)
suy ra r = \(\frac{{{S_{xq}}}}{{\pi .n}} = \frac{{240\pi }}{{\pi .20}} = 12\)cm.
Từ đó, ta có chiều cao của hình nón là:
\(\sqrt {{{20}^2} - {{12}^2}} = 16\) cm (Theo định lý Pythagore).
Trả lời câu hỏi Vận dụng 2 trang 72 SGK Toán 9 Cùng khám phá
Nón lá phổ biến ở cả ba miền của nước ta nhưng nón lá Huế từ lâu đã trở thành nguồn cảm hứng cho thi ca. Nón Huế thường có màu trắng xanh, thanh tao, mỏng, nhẹ, mềm mại. Nón lá Huế có khung gồm 16 vòng cách đều nhau (khuôn nón còn được gọi là khung chằm) và được lợp bằng nhiều lớp lá của cây lá nón trồng ở huyện A Lưới và huyện Nam Đông, thuộc tỉnh Thừa Thiên Huế. Tính diện tích bề mặt ngoài (theo centimet vuông) của một chiếc nón lá có đường kính đáy 41 cm và chiều cao 18 cm (làm tròn kết quả đến hàng phần mười).
Phương pháp giải:
Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rn\) (với r là bán kính đáy và n là đường sinh của hình nón).
Lời giải chi tiết:
Ta có đường sinh của chiếc nón lá là:
\(\sqrt {{{\left( {\frac{{41}}{2}} \right)}^2} + {{18}^2}} \approx 27,3\) cm (theo định lí pythagore)
Vậy diện tích bề mặt ngoài của chiếc nón lá là:
\({S_{xq}} = \pi rn = \pi .\frac{{41}}{2}.27,3 \approx 1758,2\)cm2
Trả lời câu hỏi Hoạt động 2 trang 71 SGK Toán 9 Cùng khám phá
Cắt mặt xung quanh của một hình nón có đường sinh dài 6 cm, bán kính đáy 2 cm (Hình 9.22a) dọc theo đường sinh SA của nó rồi trải phẳng ra, ta được hình khai triển của hình nón đó (Hình 9.22b).
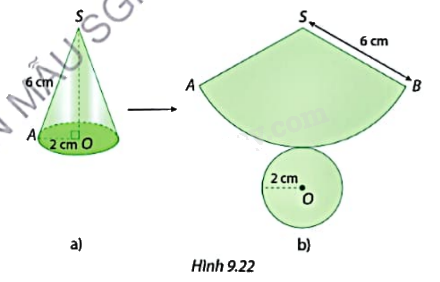
a) Tính chu vi đáy của hình nón, từ đó cho biết độ dài cung ứng với hình quạt tròn ở Hình 9.22b.
b) Tính diện tích của hình quạt tròn khai triển trong Hình 9.22b.
Phương pháp giải:
Chu vi đường tròn: C = \(\pi {r^2}\)(r là bán kính đường tròn).
Lời giải chi tiết:
a) Chu vi đáy hình nón là:
\(\pi {r^2} = 4\pi \)(cm).
Suy ra độ dài cung ứng với hình quạt tròn là: \(r.n\) (n: số đo góc ở tâm chắn cung đó).
b) Diện tích hình quạt tròn khai triển là:
S = \(\frac{{\pi .{r^2}.n}}{{360}}\).
Mục 2 trang 71, 72 SGK Toán 9 tập 2 thường xoay quanh các chủ đề về hàm số bậc nhất và ứng dụng của nó. Để giải quyết các bài tập trong mục này, học sinh cần nắm vững các khái niệm cơ bản như:
Các bài tập loại này yêu cầu học sinh xác định xem một biểu thức có phải là hàm số bậc nhất hay không, và nếu có thì xác định hệ số a và b. Ví dụ:
Cho biểu thức y = 2x - 3. Hãy xác định xem đây có phải là hàm số bậc nhất hay không? Nếu có, hãy xác định hệ số a và b.
Giải: Đây là hàm số bậc nhất với a = 2 và b = -3.
Để vẽ đồ thị hàm số bậc nhất, ta thực hiện các bước sau:
Ví dụ: Vẽ đồ thị hàm số y = x + 1.
Giải:
Các bài toán thực tế thường yêu cầu học sinh xây dựng hàm số bậc nhất để mô tả mối quan hệ giữa các đại lượng, sau đó sử dụng hàm số để giải quyết bài toán. Ví dụ:
Một người nông dân có một mảnh đất hình chữ nhật. Chiều dài của mảnh đất là 20m, chiều rộng là 10m. Người nông dân muốn tăng chiều dài của mảnh đất thêm x mét. Hãy viết hàm số biểu thị diện tích của mảnh đất sau khi tăng chiều dài.
Giải:
Diện tích của mảnh đất sau khi tăng chiều dài là: S = (20 + x) * 10 = 200 + 10x. Vậy hàm số biểu thị diện tích của mảnh đất là S(x) = 200 + 10x.
Việc nắm vững kiến thức về hàm số bậc nhất và ứng dụng của nó là rất quan trọng đối với học sinh lớp 9. Hy vọng rằng với bài giải chi tiết và các ví dụ minh họa trên, các em sẽ tự tin hơn trong quá trình học tập và giải bài tập Toán 9. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán nhé!