Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 1 trang 75 và 76 sách giáo khoa Toán 9 tập 1.
Mục tiêu của chúng ta là nắm vững kiến thức, hiểu rõ phương pháp giải và áp dụng thành thạo vào các bài tập tương tự. Hãy cùng bắt đầu!
1. Vẽ một góc nhọn có số đo (alpha ) bất kì. Chọn một điểm C trên một cạnh và vẽ đường vuông góc CA từ C xuống cạnh còn lại (Hình 4.3). Hãy đo và tính các tỉ số cạnh đối và cạnh huyền, cạnh kề và cạnh huyền, cạnh đối và cạnh kề của góc B trong tam giác ABC. 2. Vẽ thêm một góc nhọn B’ cũng có số đo (alpha ) như trên và thực hiện tương tự. 3. Sử dụng dấu hiệu đồng dạng của hai tam giác vuông, hãy giải thích vì sao các cặp tỉ số tương ứng của (widehat B) và (widehat {B'}) bằng nhau.
Trả lời câu hỏi Luyện tập 1 trang 76 SGK Toán 9 Cùng khám phá
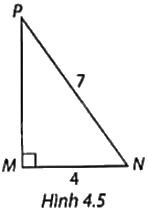
Tính các tỉ số lượng giác của góc N và góc P trong Hình 4.5.
Phương pháp giải:
Trong tam giác vuông có góc nhọn \(\alpha \), khi đó:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là \(\sin \alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là \(\cos \alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là \(\tan \alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là \(\cot \alpha \).
Lời giải chi tiết:
Tam giác MNP vuông tại M nên \(M{P^2} + M{N^2} = N{P^2}\) (Định lí Pythagore).
Suy ra: \(M{P^2} = N{P^2} - M{N^2} = {7^2} - {4^2} = 33\). Do đó, \(MP = \sqrt {33} \).
Do đó, \(\sin N = \frac{{MP}}{{PN}} = \frac{{\sqrt {33} }}{7}\), \(\cos N = \frac{{MN}}{{PN}} = \frac{4}{7}\), \(\tan N = \frac{{MP}}{{MN}} = \frac{{\sqrt {33} }}{4}\), \(\cot N = \frac{{MN}}{{MP}} = \frac{4}{{\sqrt {33} }}\).
\(\sin P = \frac{{MN}}{{PN}} = \frac{4}{7}\), \(\cos P = \frac{{MP}}{{PN}} = \frac{{\sqrt {33} }}{7}\), \(\tan P = \frac{{MN}}{{MP}} = \frac{4}{{\sqrt {33} }}\), \(\cot P = \frac{{MP}}{{MN}} = \frac{{\sqrt {33} }}{4}\).
Trả lời câu hỏi Hoạt động 1 trang 75 SGK Toán 9 Cùng khám phá
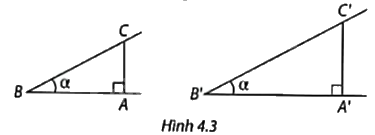
1. Vẽ một góc nhọn có số đo \(\alpha \) bất kì. Chọn một điểm C trên một cạnh và vẽ đường vuông góc CA từ C xuống cạnh còn lại (Hình 4.3). Hãy đo và tính các tỉ số cạnh đối và cạnh huyền, cạnh kề và cạnh huyền, cạnh đối và cạnh kề của góc B trong tam giác ABC.
2. Vẽ thêm một góc nhọn B’ cũng có số đo \(\alpha \) như trên và thực hiện tương tự.
3. Sử dụng dấu hiệu đồng dạng của hai tam giác vuông, hãy giải thích vì sao các cặp tỉ số tương ứng của \(\widehat B\) và \(\widehat {B'}\) bằng nhau.
Phương pháp giải:
Chứng minh tam giác ABC đồng dạng với tam giác A’B’C’ theo trường hợp góc – góc, từ đó suy ra các cặp tỉ số tương ứng của \(\widehat B\) và \(\widehat {B'}\) bằng nhau.
Lời giải chi tiết:
1. Ta đo được \(AB = 1,6cm,AC = 0,8cm,BC = 1,8cm\).
Tỉ số cạnh đối và cạnh huyền của góc B là:
\(\frac{{CA}}{{BC}} = \frac{{0,8}}{{1,8}} = \frac{4}{9}\).
Tỉ số cạnh kề và cạnh huyền của góc B là:
\(\frac{{BA}}{{BC}} = \frac{{1,6}}{{1,8}} = \frac{8}{9}\).
Tỉ số cạnh đối và cạnh kề của góc B là:
\(\frac{{CA}}{{AB}} = \frac{{0,8}}{{1,6}} = \frac{1}{2}\).
2. Ta đo được \(A'B' = 2,4cm,A'C' = 1,2cm,BC = 2,7cm\).
Tỉ số cạnh đối và cạnh huyền của góc B’ là:
\(\frac{{C'A'}}{{B'C'}} = \frac{{1,2}}{{2,7}} = \frac{4}{9}\).
Tỉ số cạnh kề và cạnh huyền của góc B’ là:
\(\frac{{B'A'}}{{B'C'}} = \frac{{2,4}}{{2,7}} = \frac{8}{9}\).
Tỉ số cạnh đối và cạnh kề của góc B’ là:
\(\frac{{C'A'}}{{A'B'}} = \frac{{1,2}}{{2,4}} = \frac{1}{2}\).
Trả lời câu hỏi Hoạt động 1 trang 75 SGK Toán 9 Cùng khám phá
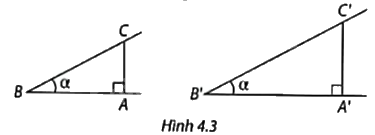
1. Vẽ một góc nhọn có số đo \(\alpha \) bất kì. Chọn một điểm C trên một cạnh và vẽ đường vuông góc CA từ C xuống cạnh còn lại (Hình 4.3). Hãy đo và tính các tỉ số cạnh đối và cạnh huyền, cạnh kề và cạnh huyền, cạnh đối và cạnh kề của góc B trong tam giác ABC.
2. Vẽ thêm một góc nhọn B’ cũng có số đo \(\alpha \) như trên và thực hiện tương tự.
3. Sử dụng dấu hiệu đồng dạng của hai tam giác vuông, hãy giải thích vì sao các cặp tỉ số tương ứng của \(\widehat B\) và \(\widehat {B'}\) bằng nhau.
Phương pháp giải:
Chứng minh tam giác ABC đồng dạng với tam giác A’B’C’ theo trường hợp góc – góc, từ đó suy ra các cặp tỉ số tương ứng của \(\widehat B\) và \(\widehat {B'}\) bằng nhau.
Lời giải chi tiết:
1. Ta đo được \(AB = 1,6cm,AC = 0,8cm,BC = 1,8cm\).
Tỉ số cạnh đối và cạnh huyền của góc B là:
\(\frac{{CA}}{{BC}} = \frac{{0,8}}{{1,8}} = \frac{4}{9}\).
Tỉ số cạnh kề và cạnh huyền của góc B là:
\(\frac{{BA}}{{BC}} = \frac{{1,6}}{{1,8}} = \frac{8}{9}\).
Tỉ số cạnh đối và cạnh kề của góc B là:
\(\frac{{CA}}{{AB}} = \frac{{0,8}}{{1,6}} = \frac{1}{2}\).
2. Ta đo được \(A'B' = 2,4cm,A'C' = 1,2cm,BC = 2,7cm\).
Tỉ số cạnh đối và cạnh huyền của góc B’ là:
\(\frac{{C'A'}}{{B'C'}} = \frac{{1,2}}{{2,7}} = \frac{4}{9}\).
Tỉ số cạnh kề và cạnh huyền của góc B’ là:
\(\frac{{B'A'}}{{B'C'}} = \frac{{2,4}}{{2,7}} = \frac{8}{9}\).
Tỉ số cạnh đối và cạnh kề của góc B’ là:
\(\frac{{C'A'}}{{A'B'}} = \frac{{1,2}}{{2,4}} = \frac{1}{2}\).
Trả lời câu hỏi Luyện tập 1 trang 76 SGK Toán 9 Cùng khám phá
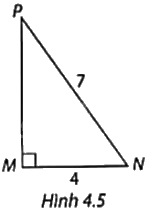
Tính các tỉ số lượng giác của góc N và góc P trong Hình 4.5.
Phương pháp giải:
Trong tam giác vuông có góc nhọn \(\alpha \), khi đó:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là \(\sin \alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là \(\cos \alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là \(\tan \alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là \(\cot \alpha \).
Lời giải chi tiết:
Tam giác MNP vuông tại M nên \(M{P^2} + M{N^2} = N{P^2}\) (Định lí Pythagore).
Suy ra: \(M{P^2} = N{P^2} - M{N^2} = {7^2} - {4^2} = 33\). Do đó, \(MP = \sqrt {33} \).
Do đó, \(\sin N = \frac{{MP}}{{PN}} = \frac{{\sqrt {33} }}{7}\), \(\cos N = \frac{{MN}}{{PN}} = \frac{4}{7}\), \(\tan N = \frac{{MP}}{{MN}} = \frac{{\sqrt {33} }}{4}\), \(\cot N = \frac{{MN}}{{MP}} = \frac{4}{{\sqrt {33} }}\).
\(\sin P = \frac{{MN}}{{PN}} = \frac{4}{7}\), \(\cos P = \frac{{MP}}{{PN}} = \frac{{\sqrt {33} }}{7}\), \(\tan P = \frac{{MN}}{{MP}} = \frac{4}{{\sqrt {33} }}\), \(\cot P = \frac{{MP}}{{MN}} = \frac{{\sqrt {33} }}{4}\).
Mục 1 của chương trình Toán 9 tập 1 thường tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc nhất. Các bài tập trong trang 75 và 76 SGK thường xoay quanh việc xác định hàm số, vẽ đồ thị hàm số, và giải các bài toán liên quan đến ứng dụng của hàm số bậc nhất trong thực tế.
Trước khi đi vào giải các bài tập cụ thể, chúng ta cần ôn lại một số kiến thức cơ bản về hàm số bậc nhất:
Các bài tập trang 75 thường yêu cầu học sinh xác định các hệ số a và b của hàm số, vẽ đồ thị hàm số, và tìm các điểm đặc biệt trên đồ thị.
Ví dụ: Cho hàm số y = 2x - 3. Hãy xác định hệ số a và b, vẽ đồ thị hàm số, và tìm giao điểm của đồ thị với trục Ox và trục Oy.
Các bài tập trang 76 thường liên quan đến việc giải các bài toán thực tế bằng cách sử dụng hàm số bậc nhất. Ví dụ, bài toán về quãng đường đi được của một vật chuyển động đều.
Ví dụ: Một ô tô đi từ A đến B với vận tốc 60km/h. Hãy viết hàm số biểu thị quãng đường đi được của ô tô theo thời gian và tính quãng đường ô tô đi được sau 2 giờ.
Để nắm vững kiến thức và kỹ năng giải bài tập, các em nên luyện tập thêm với các bài tập tương tự trong sách bài tập và các đề thi thử. Giaitoan.edu.vn cung cấp nhiều bài tập luyện tập khác với các mức độ khó khác nhau để các em có thể rèn luyện và nâng cao khả năng của mình.
Việc giải các bài tập trong mục 1 trang 75, 76 SGK Toán 9 tập 1 là bước quan trọng để các em nắm vững kiến thức về hàm số bậc nhất. Hy vọng với những hướng dẫn chi tiết và các ví dụ minh họa trên, các em sẽ tự tin hơn trong việc giải các bài tập Toán 9.