Chào mừng các em học sinh đến với bài giải bài tập 4.19 trang 89 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương Hàm số bậc nhất và là một phần quan trọng trong việc củng cố kiến thức về hàm số.
Chúng tôi sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và áp dụng vào các bài tập tương tự.
Làm tròn số đo góc đến phút và độ dài đến hàng phần mười của đơn vị đo độ dài được cho. Khi tia sáng được truyền qua mặt phân cách giữa không khí và nước thì đường đi tia sáng sẽ bị lệch đi do hiện tượng khúc xạ ánh sáng. Góc tới i và góc khúc xạ r như Hình 4.33 liên hệ với nhau theo công thức \(\frac{{\sin i}}{{\sin r}} = \frac{3}{4}\). Một con cá bơi ở vị trí C. Do ánh sáng bị khúc xạ nên Minh đứng trên bờ nhìn xuống nước với góc \(r = {54^o}\) thì thấy con cá ở vị trí A thẳng hàng với O, M v
Đề bài
Làm tròn số đo góc đến phút và độ dài đến hàng phần mười của đơn vị đo độ dài được cho.
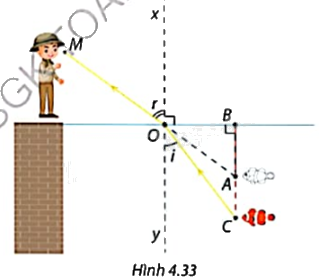
Khi tia sáng được truyền qua mặt phân cách giữa không khí và nước thì đường đi tia sáng sẽ bị lệch đi do hiện tượng khúc xạ ánh sáng. Góc tới i và góc khúc xạ r như Hình 4.33 liên hệ với nhau theo công thức \(\frac{{\sin i}}{{\sin r}} = \frac{3}{4}\). Một con cá bơi ở vị trí C. Do ánh sáng bị khúc xạ nên Minh đứng trên bờ nhìn xuống nước với góc \(r = {54^o}\) thì thấy con cá ở vị trí A thẳng hàng với O, M và cách mặt nước một đoạn \(AB = 71cm\).
a) Tính góc tới i.
b) Tính độ sâu BC từ mặt nước đến vị trí thực sự mà con cá đang bơi.
Phương pháp giải - Xem chi tiết
a) Ta có: \(\frac{{\sin i}}{{\sin r}} = \frac{3}{4}\) nên \(\sin i = \frac{3}{4}\sin r\), do đó tính được góc tới i.
b) Ta có: \(\widehat {yOA} = \hat r = {54^o}\), \(\widehat {AOB} = {90^o} - \widehat {yOA} = {36^o}\), \(\widehat {BOC} = {90^o} - \hat i\).
Tam giác AOB vuông tại B nên \(OB = AB.\cot \widehat {AOB}\).
Tam giác CBO vuông tại B nên \(BC = OB.\tan \widehat {BOC}\).
Lời giải chi tiết
a) Ta có: \(\frac{{\sin i}}{{\sin r}} = \frac{3}{4}\) nên \(\sin i = \frac{3}{4}\sin r = \frac{3}{4}\sin {54^o} \approx 0,6\), do đó, \(\widehat i \approx {37^o}21'\).
b) Ta có: \(\widehat {yOA} = \hat r = {54^o}\), \(\widehat {AOB} = {90^o} - \widehat {yOA} = {36^o}\), \(\widehat {BOC} = {90^o} - \hat i \approx {52^o}39'\)
Tam giác AOB vuông tại B nên
\(OB = AB.\cot \widehat {AOB} = 71.\cot {36^o} \approx 97,7\left( {cm} \right)\)
Tam giác CBO vuông tại B nên
\(BC = OB.\tan \widehat {BOC} \approx 97,7.\tan {52^o}39' \approx 128\left( {cm} \right)\)
Vậy độ sâu từ mặt nước đến vị trí thực sự mà con cá đang bơi là khoảng 128cm.
Bài tập 4.19 trang 89 SGK Toán 9 tập 1 yêu cầu chúng ta xét hàm số y = (m-2)x + 3. Để hàm số này là hàm số bậc nhất, điều kiện cần và đủ là hệ số của x khác 0, tức là m-2 ≠ 0. Bài viết này sẽ đi sâu vào phân tích điều kiện này và cách xác định giá trị của m để đảm bảo hàm số thỏa mãn yêu cầu.
Hàm số y = ax + b được gọi là hàm số bậc nhất khi và chỉ khi a ≠ 0. Trong trường hợp bài tập này, a = m-2. Do đó, để y = (m-2)x + 3 là hàm số bậc nhất, chúng ta cần có:
m - 2 ≠ 0
Giải phương trình này, ta được:
m ≠ 2
Điều kiện m ≠ 2 có nghĩa là giá trị của m không thể bằng 2. Nếu m = 2, hàm số sẽ trở thành y = (2-2)x + 3 = 0x + 3 = 3, đây là một hàm số hằng, không phải hàm số bậc nhất. Do đó, để đảm bảo hàm số là bậc nhất, m phải khác 2.
Xét một số trường hợp cụ thể:
Hàm số bậc nhất có dạng y = ax + b, trong đó a là hệ số góc và b là tung độ gốc. Hệ số góc a quyết định độ dốc của đường thẳng biểu diễn hàm số. Nếu a > 0, đường thẳng đi lên từ trái sang phải. Nếu a < 0, đường thẳng đi xuống từ trái sang phải. Tung độ gốc b là giao điểm của đường thẳng với trục Oy.
Để củng cố kiến thức, các em có thể thử giải các bài tập tương tự sau:
Khi giải các bài tập về hàm số bậc nhất, các em cần chú ý:
Bài tập 4.19 trang 89 SGK Toán 9 tập 1 là một bài tập cơ bản nhưng quan trọng trong việc hiểu và vận dụng kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và các phân tích trên, các em đã nắm vững phương pháp giải và có thể tự tin giải quyết các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!