Chào mừng các em học sinh đến với bài giải bài tập 5.11 trang 109 SGK Toán 9 tập 1 của giaitoan.edu.vn. Bài tập này thuộc chương Hàm số bậc nhất và là một phần quan trọng trong việc củng cố kiến thức về hàm số.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và áp dụng vào các bài tập tương tự.
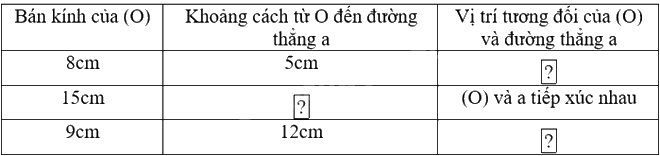
Thay các ô ? trong bảng dưới đây bằng một độ dài hoặc một khẳng định thích hợp.
Đề bài
Thay các ô ? trong bảng dưới đây bằng một độ dài hoặc một khẳng định thích hợp.
Phương pháp giải - Xem chi tiết
Cho đường tròn (O; R) và đường thẳng a. Đặt d là khoảng cách từ O đến đường thẳng a. Vị trí tương đối của đường thẳng a và đường tròn (O; R) có thể được xác định dựa vào mối quan hệ giữa R và d như sau:
+ Nếu \(d > R\) thì đường thẳng a và đường tròn (O) không giao nhau.
+ Nếu \(d = R\) thì đường thẳng a và đường tròn (O) tiếp xúc nhau.
+ Nếu \(d < R\) thì đường thẳng a và đường tròn (O) cắt nhau.
Lời giải chi tiết

Bài tập 5.11 trang 109 SGK Toán 9 tập 1 yêu cầu tìm phương trình đường thẳng là tiếp tuyến của đồ thị hàm số y = -2x + 3 tại điểm có hoành độ x = 1.
Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:
a) Tìm f(x0) và f'(x0)
Với hàm số y = -2x + 3 và x0 = 1, ta có:
b) Viết phương trình tiếp tuyến
Áp dụng công thức phương trình tiếp tuyến, ta có:
y = f'(x0)(x - x0) + f(x0)
y = -2(x - 1) + 1
y = -2x + 2 + 1
y = -2x + 3
Vậy, phương trình đường thẳng là tiếp tuyến của đồ thị hàm số y = -2x + 3 tại điểm có hoành độ x = 1 là y = -2x + 3.
Kết quả cho thấy, trong trường hợp này, tiếp tuyến tại điểm x = 1 chính là bản thân đường thẳng y = -2x + 3. Điều này là do điểm x = 1 nằm trên đường thẳng và đạo hàm của hàm số là một hằng số.
Để hiểu rõ hơn về tiếp tuyến, các em có thể tìm hiểu thêm về các bài tập tương tự với các hàm số phức tạp hơn, ví dụ như hàm số bậc hai hoặc hàm số lượng giác.
Dưới đây là một số bài tập tương tự để các em luyện tập:
Hy vọng bài giải này sẽ giúp các em hiểu rõ hơn về cách giải bài tập 5.11 trang 109 SGK Toán 9 tập 1. Chúc các em học tập tốt!
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.