Chào mừng các em học sinh đến với bài giải bài tập 7.20 trang 39 SGK Toán 9 tập 2 trên giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán. Đồng thời, chúng tôi cũng cung cấp các bài tập tương tự để các em luyện tập và củng cố kiến thức.
Tam giác ABC có \(\widehat B = {76^o},\widehat C = {40^o}\). Đường tròn (O) nội tiếp \(\Delta \)ABC tiếp xúc với các cạnh AB, BC, AC lần lượt tại các điểm M, N, P. a) Chứng minh AMOP, BMON và CNOP là các tứ giác nội tiếp. b) Tính số đo cung nhỏ MN, NP và MP. c) Tính các góc của \(\Delta \)MNP.
Đề bài
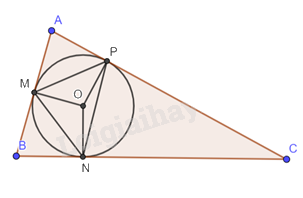
Tam giác ABC có \(\widehat B = {76^o},\widehat C = {40^o}\). Đường tròn (O) nội tiếp \(\Delta \)ABC tiếp xúc với các cạnh AB, BC, AC lần lượt tại các điểm M, N, P.
a) Chứng minh AMOP, BMON và CNOP là các tứ giác nội tiếp.
b) Tính số đo cung nhỏ MN, NP và MP.
c) Tính các góc của \(\Delta \)MNP.
Phương pháp giải - Xem chi tiết
Đọc kĩ dữ liệu đề bài để vẽ hình.
Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm của đường tròn đó.
Nếu một tứ giác có tổng số đo hai góc đối diện bằng 180° thì tứ giác đó nội tiếp được đường tròn.
Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
Góc nội tiếp bằng nửa số đo của góc ở tâm cùng chắn một cung.
Lời giải chi tiết
a) Xét tứ giác AMOP có \(\widehat {BMO} + \widehat {BNO} = {90^o} + {90^o} = {180^o}\)(tính chất tiếp tuyến)
Suy ra tứ giác AMOP nội tiếp.
Chứng minh tương tự ta có BMON và CNOP là các tứ giác nội tiếp.
b) Ta có \(\widehat {MON} = {180^o} - \widehat {MBN} = {180^o} - {76^o} = {104^o}\) (do BMON nội tiếp)
Suy ra \(sđ\overset\frown{MN}=\widehat{MON}={{104}^{o}}\) (Tính chất góc ở tâm)
Ta có \(\widehat {NOP} = {180^o} - \widehat {PCN} = {180^o} - {40^o} = {140^o}\)(do CNOP nội tiếp)
Suy ra \(sđ\overset\frown{NP}=\widehat{NOP}={{140}^{o}}\) (Tính chất góc ở tâm)
Suy ra \(sđ\overset\frown{MP}={{360}^{o}}-sđ\overset\frown{NP}-sđ\overset\frown{MN}={{360}^{o}}-{{140}^{o}}-{{104}^{o}}={{116}^{o}}\)
c) Xét tam giác MNP:
Ta có \(\widehat {NMP} = \frac{1}{2}\widehat {NOP} = \frac{1}{2}{.140^o} = {70^o}\) (góc nội tiếp bằng nửa góc ở tâm cùng chắn cung nhỏ NP)
\(\widehat {MPN} = \frac{1}{2}\widehat {MON} = \frac{1}{2}{.104^o} = {52^o}\) (góc nội tiếp bằng nửa góc ở tâm cùng chắn cung nhỏ MN)
\(\widehat {MNP} = {180^o} - \widehat {NMP} - \widehat {MPN} = {180^o} - {70^o} - {52^o} = {58^o}\)
Bài tập 7.20 trang 39 SGK Toán 9 tập 2 yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết một bài toán thực tế liên quan đến việc xác định phương trình đường thẳng và ứng dụng của nó. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm và công thức sau:
Bài tập 7.20 thường đưa ra một tình huống thực tế, ví dụ như việc xác định phương trình đường thẳng đi qua hai điểm cho trước, hoặc đường thẳng song song/vuông góc với một đường thẳng khác. Để giải bài toán, chúng ta cần:
Giả sử bài tập yêu cầu tìm phương trình đường thẳng đi qua hai điểm A(1; 2) và B(3; 4). Chúng ta có thể giải như sau:
Ngoài bài tập 7.20, còn rất nhiều bài tập tương tự trong SGK Toán 9 tập 2. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải:
Để nắm vững kiến thức về hàm số bậc nhất và ứng dụng, các em nên luyện tập thêm các bài tập khác trong SGK và sách bài tập. Ngoài ra, các em có thể tham khảo các tài liệu học tập trực tuyến trên giaitoan.edu.vn để có thêm nhiều bài tập và lời giải chi tiết.
Bài tập 7.20 trang 39 SGK Toán 9 tập 2 là một bài tập quan trọng giúp các em củng cố kiến thức về hàm số bậc nhất và ứng dụng. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, các em có thể giải bài tập này một cách dễ dàng và hiệu quả. Chúc các em học tập tốt!
| Khái niệm | Công thức |
|---|---|
| Hệ số góc | a = (y2 - y1) / (x2 - x1) |
| Phương trình đường thẳng | y = ax + b |
| Điều kiện song song | a1 = a2 |
| Điều kiện vuông góc | a1 * a2 = -1 |