Chào mừng bạn đến với bài học về lý thuyết đường tròn ngoại tiếp và nội tiếp tam giác trong chương trình Toán 9. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về hai loại đường tròn đặc biệt này, cùng với các ứng dụng thực tế trong giải toán.
Chúng ta sẽ cùng nhau khám phá định nghĩa, tính chất, cách xác định tâm và bán kính của đường tròn ngoại tiếp và nội tiếp, cũng như mối liên hệ giữa chúng với các yếu tố của tam giác.
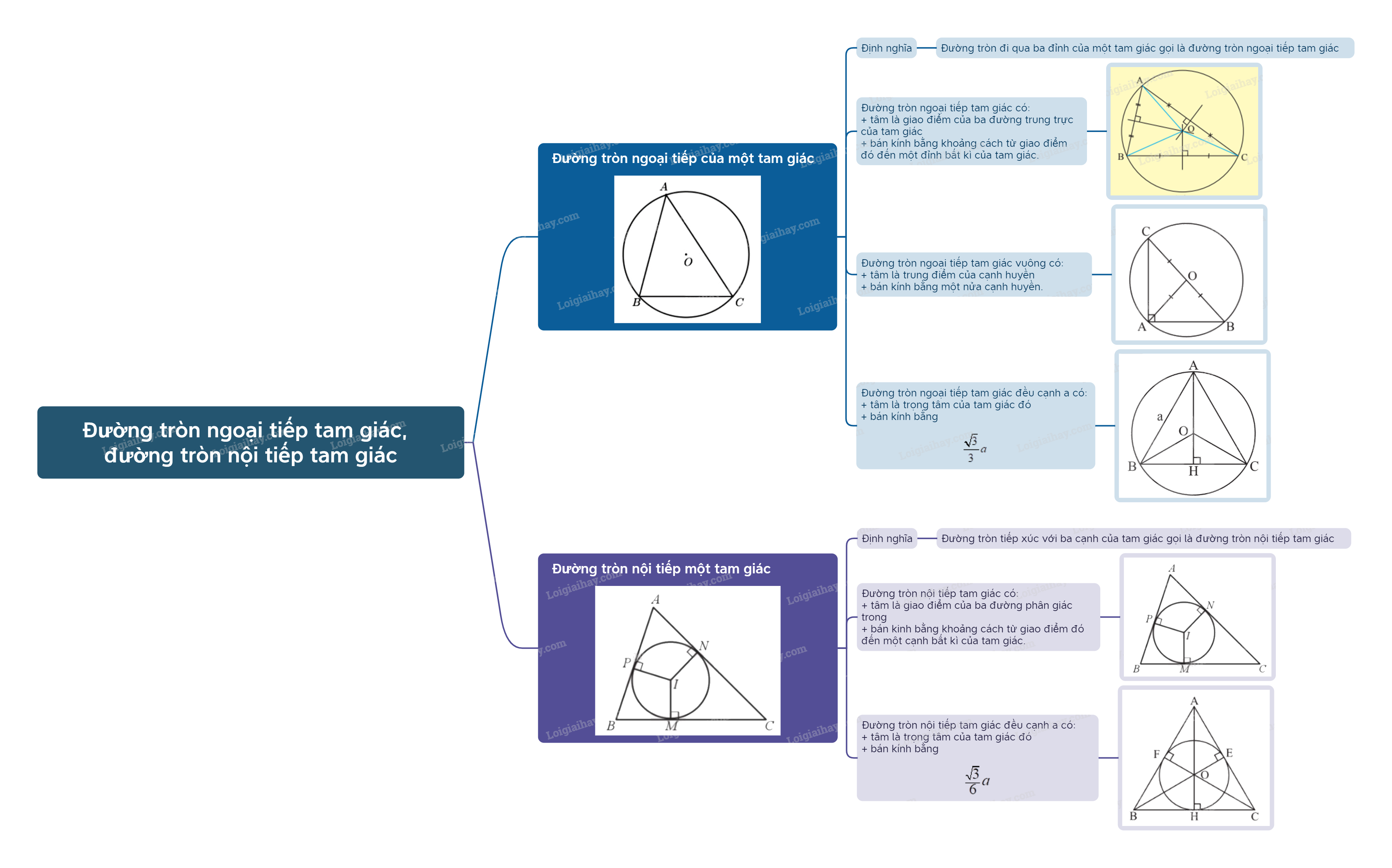
1. Đường tròn ngoại tiếp tam giác Định nghĩa đường tròn ngoại tiếp tam giác – Đường tròn đi qua ba đỉnh của một tam giác gọi là đường tròn ngoại tiếp tam giác, khi đó tam giác được gọi là tam giác nội tiếp đường tròn. – Tâm của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó. Bán kính của đường tròn ngoại tiếp tam giác là khoảng cách từ giao điểm này đến một đỉnh bất kì của tam giác.
1. Đường tròn ngoại tiếp tam giác
Định nghĩa đường tròn ngoại tiếp tam giác
– Đường tròn đi qua ba đỉnh của một tam giác gọi là đường tròn ngoại tiếp tam giác, khi đó tam giác được gọi là tam giác nội tiếp đường tròn. – Tâm của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó. Bán kính của đường tròn ngoại tiếp tam giác là khoảng cách từ giao điểm này đến một đỉnh bất kì của tam giác.
|
Ví dụ:
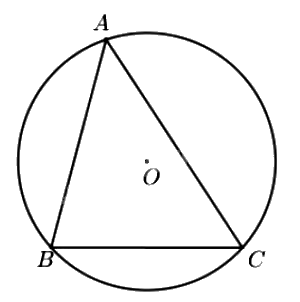
- Đường tròn (O) ngoại tiếp tam giác ABC. Tam giác ABC nội tiếp đường tròn (O).
- Tâm O là giao điểm của ba đường trung trực của tam giác ABC.
Đường tròn ngoại tiếp tam giác vuông
Đường tròn ngoại tiếp tam giác vuông có tâm là trung điểm của cạnh huyền và bán kính bằng một nửa cạnh huyền.
|
Ví dụ:
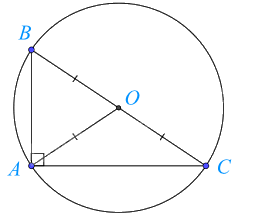
Tam giác ABC nội tiếp đường tròn (O; BO).
Đường tròn ngoại tiếp tam giác đều
Đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{3}a\).
|
Ví dụ:
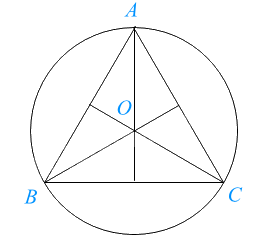
Đường tròn (O) ngoại tiếp tam giác đều ABC, bán kính \(OA = OB = OC = \frac{{\sqrt 3 }}{3}AB\).
2. Đường tròn nội tiếp một tam giác
Định nghĩa đường tròn nội tiếp tam giác
- Đường tròn tiếp xúc với ba cạnh của tam giác gọi là đường tròn nội tiếp tam giác, khi đó tam giác được gọi là tam giác ngoại tiếpđường tròn. - Đường tròn nội tiếp tam giác có tâm là giao điểm của ba đường phân giác trong và bán kính bằng khoảng cách từ giao điểm đó đến một cạnh bất kì của tam giác.
|
Ví dụ:
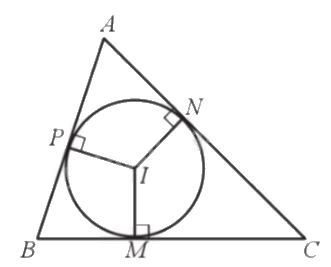
- Đường tròn (I) nội tiếp tam giác ABC. Tam giác ABC ngoại tiếp đường tròn (I).
- Tâm I là giao điểm của ba đường phân giác của tam giác.
Đường tròn nội tiếp tam giác đều
Đường tròn nội tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{6}a\).
|
Ví dụ:
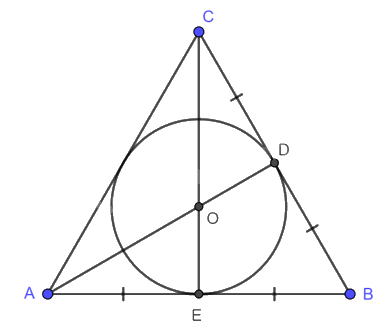
Đường tròn (O) nội tiếp tam giác đều ABC, bán kính \(OD = OE = \frac{{\sqrt 3 }}{6}AB\).
Trong hình học, đường tròn đóng vai trò quan trọng trong việc nghiên cứu các tính chất và mối quan hệ giữa các điểm và đường thẳng. Đặc biệt, đường tròn ngoại tiếp và nội tiếp tam giác là hai khái niệm cơ bản và thường xuyên xuất hiện trong các bài toán hình học lớp 9.
Định nghĩa: Đường tròn ngoại tiếp tam giác là đường tròn đi qua ba đỉnh của tam giác đó.
Tâm đường tròn ngoại tiếp: Giao điểm của các đường trung trực của tam giác.
Bán kính đường tròn ngoại tiếp (R): Khoảng cách từ tâm đường tròn ngoại tiếp đến một đỉnh của tam giác.
Công thức tính R:
a/(2sinA) = b/(2sinB) = c/(2sinC) (với a, b, c là độ dài các cạnh, A, B, C là các góc đối diện)abc/(4S) (với S là diện tích tam giác)Tính chất:
Định nghĩa: Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với cả ba cạnh của tam giác đó.
Tâm đường tròn nội tiếp: Giao điểm của các đường phân giác của tam giác.
Bán kính đường tròn nội tiếp (r): Khoảng cách từ tâm đường tròn nội tiếp đến một cạnh của tam giác.
Công thức tính r:
2S/(a+b+c) (với S là diện tích tam giác, a, b, c là độ dài các cạnh)S/p (với p là nửa chu vi của tam giác: p = (a+b+c)/2)Tính chất:
Công thức Euler: d2 = R(R - 2r) (với d là khoảng cách giữa tâm đường tròn ngoại tiếp và tâm đường tròn nội tiếp).
Mối quan hệ này cho thấy sự liên kết mật thiết giữa hai loại đường tròn đặc biệt này trong một tam giác.
Lý thuyết về đường tròn ngoại tiếp và nội tiếp tam giác có nhiều ứng dụng trong giải toán hình học, đặc biệt là trong việc chứng minh các tính chất liên quan đến tam giác, tính góc, tính độ dài cạnh và diện tích tam giác.
Bài tập 1: Cho tam giác ABC vuông tại A, AB = 3cm, AC = 4cm. Tính bán kính đường tròn ngoại tiếp và nội tiếp của tam giác ABC.
Giải:
Bài tập 2:...
Hi vọng bài học này đã giúp bạn hiểu rõ hơn về lý thuyết đường tròn ngoại tiếp và nội tiếp tam giác trong chương trình Toán 9. Hãy luyện tập thêm nhiều bài tập để nắm vững kiến thức và áp dụng thành thạo vào giải toán.