Chào mừng các em học sinh đến với bài giải chi tiết mục 3 trang 60, 61 SGK Toán 9 tập 1 tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Bài học này tập trung vào việc... (nội dung giới thiệu ngắn gọn về chủ đề bài học)
Hãy chép lại và hoàn thành Bảng 3.2. Em có nhận xét gì về giá trị của \(\sqrt {\left( {x + 1} \right)\left( {x + 3} \right)} \) và \(\sqrt {x + 1} .\sqrt {x + 3} \)?
Trả lời câu hỏi Vận dụng 1 trang 61 SGK Toán 9 Cùng khám phá
Một hình chữ nhật có chiều dài là \(\sqrt {\frac{a}{3}} \) mét và chiều rộng là \(\sqrt {\frac{a}{{12}}} \) (mét) \(\left( {a > 0} \right)\). Tính diện tích của hình chữ nhật theo a.
Phương pháp giải:
+ Với hai biểu thức A và B không âm, ta có: \(\sqrt {A.B} = \sqrt A .\sqrt B \).
+ Diện tích hình chữ nhật bằng chiều dài nhân chiều rộng.
Lời giải chi tiết:
Diện tích của hình chữ nhật là:
\(\sqrt {\frac{a}{3}} .\sqrt {\frac{a}{{12}}} = \sqrt {\frac{a}{3}.\frac{a}{{12}}} = \sqrt {\frac{{{a^2}}}{{36}}} = \sqrt {{{\left( {\frac{a}{6}} \right)}^2}} = \left| {\frac{a}{6}} \right| = \frac{a}{6}\) (do \(a > 0\) nên \(\frac{a}{6} > 0\)).
Trả lời câu hỏi Luyện tập 3 trang 61 SGK Toán 9 Cùng khám phá
Rút gọn các biểu thức sau:
a) \(\sqrt {36{x^8}{{\left( {2 - y} \right)}^2}} \) với \(y \ge 2\);
b) \(\sqrt {\frac{{7z}}{3}} .\sqrt {\frac{3}{{28z}}} \) với \(z > 0\).
Phương pháp giải:
Với hai biểu thức A và B không âm, ta có: \(\sqrt {A.B} = \sqrt A .\sqrt B \).
Lời giải chi tiết:
a) \(\sqrt {36{x^8}{{\left( {2 - y} \right)}^2}} \)\( = \sqrt {36} .\sqrt {{x^8}} .\sqrt {{{\left( {2 - y} \right)}^2}} \)\( = 6.\sqrt {{{\left( {{x^4}} \right)}^2}} .\left| {2 - y} \right|\)\( = 6{x^4}\left( {y - 2} \right)\) (vì \(y \ge 2\) nên \(2 - y \le 0\))
b) \(\sqrt {\frac{{7z}}{3}} .\sqrt {\frac{3}{{28z}}} \)\( = \sqrt {\frac{{7z}}{3}.\frac{3}{{28z}}} \)\( = \sqrt {\frac{1}{4}} \)\( = \sqrt {{{\left( {\frac{1}{2}} \right)}^2}} \)\( = \frac{1}{2}\).
Trả lời câu hỏi Hoạt động 3 trang 60 SGK Toán 9 Cùng khám phá
Hãy chép lại và hoàn thành Bảng 3.2. Em có nhận xét gì về giá trị của \(\sqrt {\left( {x + 1} \right)\left( {x + 3} \right)} \) và \(\sqrt {x + 1} .\sqrt {x + 3} \)?
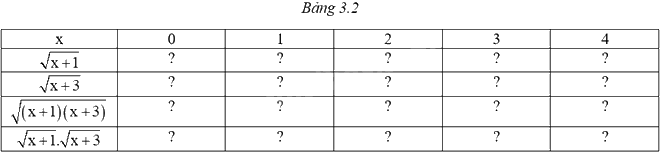
Phương pháp giải:
Thay từng giá trị của x vào các căn thức \(\sqrt {\left( {x + 1} \right)\left( {x + 3} \right)} \) và \(\sqrt {x + 1} .\sqrt {x + 3} \) để tính giá trị tương ứng, từ đó rút ra nhận xét.
Lời giải chi tiết:

Ta thấy: \(\sqrt {\left( {x + 1} \right)\left( {x + 3} \right)} = \sqrt {x + 1} .\sqrt {x + 3} \).
Trả lời câu hỏi Hoạt động 3 trang 60 SGK Toán 9 Cùng khám phá
Hãy chép lại và hoàn thành Bảng 3.2. Em có nhận xét gì về giá trị của \(\sqrt {\left( {x + 1} \right)\left( {x + 3} \right)} \) và \(\sqrt {x + 1} .\sqrt {x + 3} \)?
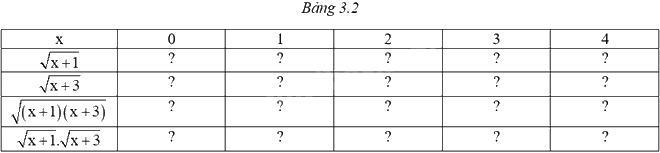
Phương pháp giải:
Thay từng giá trị của x vào các căn thức \(\sqrt {\left( {x + 1} \right)\left( {x + 3} \right)} \) và \(\sqrt {x + 1} .\sqrt {x + 3} \) để tính giá trị tương ứng, từ đó rút ra nhận xét.
Lời giải chi tiết:

Ta thấy: \(\sqrt {\left( {x + 1} \right)\left( {x + 3} \right)} = \sqrt {x + 1} .\sqrt {x + 3} \).
Trả lời câu hỏi Luyện tập 3 trang 61 SGK Toán 9 Cùng khám phá
Rút gọn các biểu thức sau:
a) \(\sqrt {36{x^8}{{\left( {2 - y} \right)}^2}} \) với \(y \ge 2\);
b) \(\sqrt {\frac{{7z}}{3}} .\sqrt {\frac{3}{{28z}}} \) với \(z > 0\).
Phương pháp giải:
Với hai biểu thức A và B không âm, ta có: \(\sqrt {A.B} = \sqrt A .\sqrt B \).
Lời giải chi tiết:
a) \(\sqrt {36{x^8}{{\left( {2 - y} \right)}^2}} \)\( = \sqrt {36} .\sqrt {{x^8}} .\sqrt {{{\left( {2 - y} \right)}^2}} \)\( = 6.\sqrt {{{\left( {{x^4}} \right)}^2}} .\left| {2 - y} \right|\)\( = 6{x^4}\left( {y - 2} \right)\) (vì \(y \ge 2\) nên \(2 - y \le 0\))
b) \(\sqrt {\frac{{7z}}{3}} .\sqrt {\frac{3}{{28z}}} \)\( = \sqrt {\frac{{7z}}{3}.\frac{3}{{28z}}} \)\( = \sqrt {\frac{1}{4}} \)\( = \sqrt {{{\left( {\frac{1}{2}} \right)}^2}} \)\( = \frac{1}{2}\).
Trả lời câu hỏi Vận dụng 1 trang 61 SGK Toán 9 Cùng khám phá
Một hình chữ nhật có chiều dài là \(\sqrt {\frac{a}{3}} \) mét và chiều rộng là \(\sqrt {\frac{a}{{12}}} \) (mét) \(\left( {a > 0} \right)\). Tính diện tích của hình chữ nhật theo a.
Phương pháp giải:
+ Với hai biểu thức A và B không âm, ta có: \(\sqrt {A.B} = \sqrt A .\sqrt B \).
+ Diện tích hình chữ nhật bằng chiều dài nhân chiều rộng.
Lời giải chi tiết:
Diện tích của hình chữ nhật là:
\(\sqrt {\frac{a}{3}} .\sqrt {\frac{a}{{12}}} = \sqrt {\frac{a}{3}.\frac{a}{{12}}} = \sqrt {\frac{{{a^2}}}{{36}}} = \sqrt {{{\left( {\frac{a}{6}} \right)}^2}} = \left| {\frac{a}{6}} \right| = \frac{a}{6}\) (do \(a > 0\) nên \(\frac{a}{6} > 0\)).
Mục 3 trang 60, 61 SGK Toán 9 tập 1 thuộc chương trình học Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Đây là một phần quan trọng, nền tảng cho các kiến thức nâng cao hơn trong chương trình học. Bài học này giúp học sinh hiểu rõ hơn về các khái niệm như hàm số, đồ thị hàm số, và cách xác định các yếu tố của hàm số.
Mục 3 bao gồm các bài tập vận dụng kiến thức về hàm số bậc nhất vào giải quyết các bài toán thực tế. Cụ thể, các bài tập thường yêu cầu:
Bài 1 yêu cầu học sinh xác định hệ số a của hàm số y = ax + b, biết đồ thị của hàm số đi qua hai điểm A(0; 2) và B(2; 6). Để giải bài này, ta thay tọa độ của hai điểm A và B vào phương trình hàm số, ta được:
Vậy hàm số cần tìm là y = 2x + 2.
Bài 2 yêu cầu học sinh vẽ đồ thị của hàm số y = -x + 3. Để vẽ đồ thị, ta thực hiện các bước sau:
Đồ thị hàm số y = -x + 3 là một đường thẳng cắt trục Oy tại điểm (0; 3) và trục Ox tại điểm (3; 0).
Ngoài các bài tập trực tiếp như trên, còn có một số dạng bài tập khác thường gặp trong mục 3, bao gồm:
Để học tốt phần hàm số bậc nhất, các em cần:
Hy vọng với bài giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ tự tin hơn khi giải các bài tập mục 3 trang 60, 61 SGK Toán 9 tập 1. Chúc các em học tập tốt và đạt kết quả cao!
| Bài tập | Mức độ khó | Gợi ý giải |
|---|---|---|
| Bài 1 (Trang 60) | Dễ | Thay tọa độ điểm vào phương trình hàm số |
| Bài 2 (Trang 61) | Trung bình | Xác định hai điểm và vẽ đồ thị |