Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các câu hỏi trong sách giáo khoa Toán 9 tập 1, trang 130, 131 và 132.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập. Hãy cùng nhau khám phá và chinh phục những bài toán thú vị này nhé!
Dựng đường phân giác góc xOy: • Vẽ đường tròn (O) cắt hai cạnh của góc xOy tại A và B; • Vẽ hai đường tròn tâm A và B có cùng bán kính cắt nhau tại điểm C khác điểm O. Khi đó, OC là tia phân giác của góc xOy. Dựng đường trung trực của đoạn thẳng AB: Vẽ hai đường tròn tâm A và tâm B có cùng bán kính lớn hơn \(\frac{1}{2}AB\) cắt nhau tại hai điểm M, N. Khi đó MN là đường trung trực của AB. Dựng đường thẳng qua điểm A và vuông góc với đường thẳng d: • Vẽ đường tròn tâm A cắt d tại hai điểm B
Trả lời câu hỏi Câu hỏi 1 trang 131SGK Toán 9 Cùng khám phá
Vẽ chắp nối trơn hai tia Ox và Oy tại điểm A thuộc Ox:
Bước 1: Dựng đường phân giác Oz của góc xOy và đường thẳng qua A vuông góc với Ox. Hai đường thẳng cắt nhau tại M.
Bước 2: Dựng đường thẳng qua M vuông góc với Oy cắt tia Oy tại B. Vẽ đường tròn tâm M đi qua A ta được cung AB nối trơn với hai tia Ox và Oy.
Vì sao với cách dựng như trên thì đường tròn (M; MA) tiếp xúc với cả hai tia Ox và Oy?
Phương pháp giải:
+ Vì \(MA \bot Ox\) tại A nên đường tròn (M; MA) tiếp xúc với tia Ox tại A.
+ Chứng minh \(\Delta MOA = \Delta MOB\left( {ch - gn} \right)\) nên \(MA = MB\) nên B thuộc đường tròn (M; MA).
+ Vì \(MB \bot Oy\) tại B nên đường tròn (M; MA) tiếp xúc với tia Oy tại B.
Lời giải chi tiết:
Vì \(MA \bot Ox\) tại A nên đường tròn (M; MA) tiếp xúc với tia Ox tại A.
Vì Oz là tia phân giác góc xOy nên \(\widehat {yOz} = \widehat {zOx}\).
Tam giác MOA và tam giác MOB có: \(\widehat {MBO} = \widehat {MAO} = {90^o},\widehat {BOM} = \widehat {MOA},OM\;chung\).
Do đó, \(\Delta MOA = \Delta MOB\left( {ch - gn} \right)\) nên \(MA = MB\) nên B thuộc đường tròn (M; MA).
Vì \(MB \bot Oy\) tại B nên đường tròn (M; MA) tiếp xúc với tia Oy tại B.
Trả lời câu hỏi Hoạt động 1 trang 130 SGK Toán 9 Cùng khám phá
Dựng đường phân giác góc xOy:
• Vẽ đường tròn (O) cắt hai cạnh của góc xOy tại A và B;
• Vẽ hai đường tròn tâm A và B có cùng bán kính cắt nhau tại điểm C khác điểm O. Khi đó, OC là tia phân giác của góc xOy.
Dựng đường trung trực của đoạn thẳng AB: Vẽ hai đường tròn tâm A và tâm B có cùng bán kính lớn hơn \(\frac{1}{2}AB\) cắt nhau tại hai điểm M, N. Khi đó MN là đường trung trực của AB.
Dựng đường thẳng qua điểm A và vuông góc với đường thẳng d:
• Vẽ đường tròn tâm A cắt d tại hai điểm B và C;
• Vẽ hai đường tròn tâm B và C có cùng bán kính cắt nhau tại điểm D khác A. Khi đó AD là đường thẳng cần dựng.
Vì sao các cách dựng trên cho ta đường phân giác, đường trung trực và đường thẳng vuông góc cần dựng?
Phương pháp giải:
+ Chứng minh cách dựng đường phân giác: Chứng minh \(\Delta BOC = \Delta AOC\left( {c.c.c} \right)\), suy ra \(\widehat {BOC} = \widehat {AOC}\) nên OC là tia phân giác của góc xOy.
+ Chứng minh đường trung trực: Chứng minh \(MA = MB,NA = NB\) nên M, N thuộc đường trung trực của AB, do đó, MN là đường trung trực của AB.
+ Chứng minh đường thẳng vuông góc: Chứng minh \(AB = AC,BD = DC\) nên A, D thuộc đường trung trực của BC. Do đó, AD là đường trung trực của BC nên AD vuông góc với BC.
Lời giải chi tiết:
+ Chứng minh cách dựng đường phân giác:
Vì B, A thuộc (O) nên \(OA = OB\).
Vì đường tròn tâm A và B có cùng bán kính và cắt nhau tại C nên \(CB = CA\).
\(\Delta \)BOC và \(\Delta \)AOC có: \(OA = OB\), \(CB = CA\), OC chung nên \(\Delta BOC = \Delta AOC\left( {c.c.c} \right)\), do đó, \(\widehat {BOC} = \widehat {AOC}\) nên OC là tia phân giác của góc xOy.
+ Chứng minh đường trung trực: Vì hai đường tròn tâm A và tâm B có cùng bán kính và cắt nhau tại M và N nên \(MA = MB,NA = NB\). Do đó, hai điểm M, N thuộc đường trung trực của AB, do đó, MN là đường trung trực của AB.
+ Chứng minh đường thẳng vuông góc:
Vì B, C thuộc (A) nên \(AB = AC\), suy ra A thuộc đường trung trực của BC.
Vì hai đường tròn tâm B và C có cùng bán kính cắt nhau tại điểm D khác A nên \(BD = DC\), suy ra D thuộc đường trung trực của BC.
Vậy AD là đường trung trực của BC. Do đó, đường thẳng AD vuông góc với BC.
Trả lời câu hỏi Câu hỏi trang 132SGK Toán 9 Cùng khám phá
Nối trơn đường thẳng xy và đường tròn (O) tại điểm A thuộc (O).
Bước 1: Vẽ tiếp tuyến của đường tròn (O) tại A, cắt xy tại điểm M.
Bước 2: Nối trơn tiếp tuyến Mz và tia My tại điểm A theo các bước ở Hoạt động 2, ta được đường nối cần dựng.
Vì sao với cách dựng như trên thì đường tròn (I; IA) tiếp xúc với đường tròn (O) và đường thẳng xy? Trong trường hợp nào hai đường tròn (O) và (I) tiếp xúc ngoài, trong trường hợp nào hai đường tròn tiếp xúc trong?
Phương pháp giải:
+ Theo cách vẽ nối trơn ở hoạt động 2 thì (I; IA) tiếp xúc với My, do đó, (I; IA) tiếp xúc với đường thẳng xy.
+ Vì Mz tiếp xúc với đường tròn (I; IA) tại A, và Mz tiếp xúc với đường tròn (O) tại A nên đường tròn (I; IA) tiếp xúc với đường tròn (O).
+ Nếu \(OA + AI = OI\) nên đường tròn (I; IA) tiếp xúc ngoài với đường tròn (O).
+ Nếu \(\left| {OA - AI} \right| = OI\) nên đường tròn (I; IA) tiếp xúc trong với đường tròn (O).
Lời giải chi tiết:
Vì (I; IA) tiếp xúc với My, do đó, (I; IA) tiếp xúc với đường thẳng xy.
Vì Mz tiếp xúc với đường tròn (I; IA) tại A, và Mz tiếp xúc với đường tròn (O) tại A nên đường tròn (I; IA) tiếp xúc với đường tròn (O).
Nếu \(OA + AI = OI\) nên đường tròn (I; IA) tiếp xúc ngoài với đường tròn (O).
Nếu \(\left| {OA - AI} \right| = OI\) nên đường tròn (I; IA) tiếp xúc trong với đường tròn (O).
Trả lời câu hỏi Câu hỏi 2 trang 133 SGK Toán 9 Cùng khám phá
Nối trơn hai đường tròn (O) và (I) từ điểm A thuộc (O).
Bước 1: Xác định điểm J trên bán kính OA sao cho AJ bằng bán kính của (I).
Bước 2: Dựng đường trung trực của IJ cắt đường thẳng OA tại M.
Bước 3: Xác định giao điểm B của MI và đường tròn (I). Vẽ đường tròn tâm M đi qua A, ta được cung AB là đường nối trơn cần dựng.
Vì sao với cách dựng như trên thì \(MA = MB\) và đường tròn (M; MA) tiếp xúc với cả hai đường tròn (O) và (I)?
Phương pháp giải:
+ Chứng minh \(MI = MJ\), \(AJ = BI\), do đó \(MJ - AJ = MI - BI\), nên \(MA = MB\).
+ Vì \(MO = AM + AO\) nên đường tròn (M; MA) tiếp xúc với đường tròn (O).
+ Vì \(MB + BI = MI\) nên đường tròn (M; MA) tiếp xúc với đường tròn (I).
Lời giải chi tiết:
Vì M thuộc đường trung trực của IJ nên \(MI = MJ\).
Vì AJ bằng bán kính (I) mà B thuộc (I) nên \(AJ = BI\).
Do đó, \(MJ - AJ = MI - BI\), nên \(MA = MB\).
Vì \(MO = AM + AO\) nên đường tròn (M; MA) tiếp xúc với đường tròn (O).
Vì \(MB + BI = MI\) nên đường tròn (M; MA) tiếp xúc với đường tròn (I).
Trả lời câu hỏi Thực hành 5 trang 134 SGK Toán 9 Cùng khám phá
Sử dụng các phương pháp dựng hình và chắp nối trơn như trên để thực hiện một thiết kế hoặc mẫu hoa văn trang trí tùy ý. Trình bày ý tưởng và mẫu thiết kế trước lớp.
Phương pháp giải:
Sử dụng các phương pháp chắp nối trơn đã nêu ở trên để vẽ.
Lời giải chi tiết:
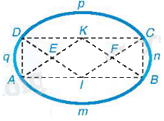
Cách vẽ hình “trái xoan”
+ Vẽ hình chữ nhật ABCD.
+ Xác định trung điểm I của đoạn thẳng AB và trung điểm K của đoạn thẳng CD.
+ Tìm giao điểm E của AK và DI; giao điểm F của BK và CI.
+ Vẽ 4 cung: Cung AmB (tâm K), cung CpD (tâm I), cung BnC (tâm F), cung DqA (tâm E).
Khi đó, bốn cung tròn vừa vẽ tạo nên hình “trái xoan”. Trong đó, tâm hai cung liên tiếp, chẳng hạn tâm K của cung AmB và tâm F của cung BnC thẳng hàng với điểm nối trơn B, chứng tỏ hai đường tròn (K) và (F) tiếp xúc nhau tại B. Khi đó, hai cung này nối trơn với nhau tại B.
Chứng minh tương tự với các cặp cung còn lại.
Trả lời câu hỏi Thực hành 2 trang 132SGK Toán 9 Cùng khám phá
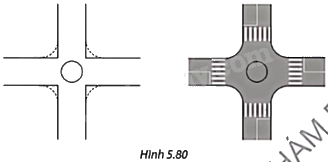
Sử dụng phương pháp nối trơn hai đường thẳng để hoàn thiện phác thảo bên trái và trang trí thành bản vẽ thiết kế ngã tư đường như trong Hình 5.80
Phương pháp giải:
Trong thiết kế và đồ họa, có các chi tiết được chắp nối với nhau bằng các cung của đường tròn. Các đường tròn này thường tiếp xúc với các chi tiết được nối với chúng sao cho đường đi không bị “gãy” mà được trơn tại điểm nối. Khi đó, ta nói các chi tiết được ghép trơn với nhau.
Lời giải chi tiết:
+ Sử dụng phương pháp nối trơn hai đường thẳng, ta vẽ được:
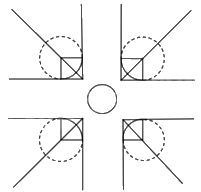
Tiến hành trang trí ta được:

Trả lời câu hỏi Thực hành 3 trang 133SGK Toán 9 Cùng khám phá
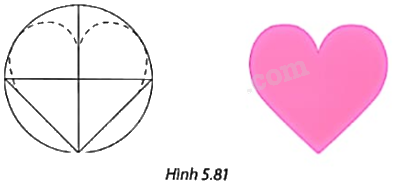
Sử dụng phương pháp nối trơn đường thẳng với đường tròn để hoàn thiện phác thảo bên trái và tô màu thành hoa văn hình trái tim như trong Hình 5.81.
Phương pháp giải:
Sử dụng phương pháp nối trơn đường thẳng với đường tròn.
Lời giải chi tiết:
+ Sử dụng phương pháp nối trơn đường thẳng với đường tròn ta phác thảo được hình trái tim:
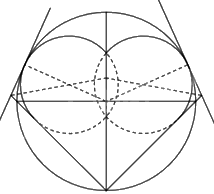
Hoàn thiện hình vẽ ta được:

Trả lời câu hỏi Thực hành 4 trang 133 SGK Toán 9 Cùng khám phá
Sử dụng phương pháp nối trơn đường tròn với đường tròn ở trên để hoàn thiện phác thảo bên trái và trang trí thành thiết kế hồ bơi trong Hình 5.82.
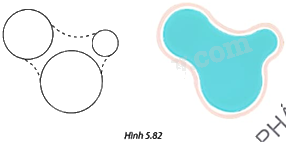
Phương pháp giải:
Sử dụng phương pháp nối trơn đường tròn với đường tròn để hoàn thiện bảng phác thảo.
Lời giải chi tiết:
Sử dụng phương pháp nối trơn đường tròn với đường tròn ta được các đường nét trơn (màu xanh):
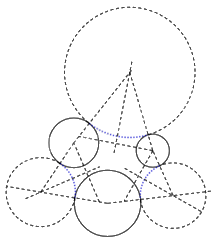
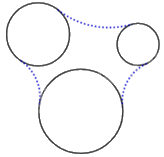
Hoàn thiện hình vẽ ta được:

Trả lời câu hỏi Thực hành 1 trang 131 SGK Toán 9 Cùng khám phá
Em hãy tìm thêm các hình ảnh về các chi tiết được chắp nối trơn trên thực tế.
Phương pháp giải:
Trong thiết kế và đồ họa, có các chi tiết được chắp nối với nhau bằng các cung của đường tròn. Các đường tròn này thường tiếp xúc với các chi tiết được nối với chúng sao cho đường đi không bị “gãy” mà được trơn tại điểm nối. Khi đó, ta nói các chi tiết được ghép trơn với nhau.
Lời giải chi tiết:
+ Đường vòng xuyến:

+ Xích xe với hai bánh xe:
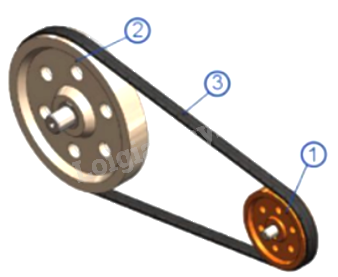
+ Vòi nước:

Trả lời câu hỏi Hoạt động 1 trang 130 SGK Toán 9 Cùng khám phá
Dựng đường phân giác góc xOy:
• Vẽ đường tròn (O) cắt hai cạnh của góc xOy tại A và B;
• Vẽ hai đường tròn tâm A và B có cùng bán kính cắt nhau tại điểm C khác điểm O. Khi đó, OC là tia phân giác của góc xOy.
Dựng đường trung trực của đoạn thẳng AB: Vẽ hai đường tròn tâm A và tâm B có cùng bán kính lớn hơn \(\frac{1}{2}AB\) cắt nhau tại hai điểm M, N. Khi đó MN là đường trung trực của AB.
Dựng đường thẳng qua điểm A và vuông góc với đường thẳng d:
• Vẽ đường tròn tâm A cắt d tại hai điểm B và C;
• Vẽ hai đường tròn tâm B và C có cùng bán kính cắt nhau tại điểm D khác A. Khi đó AD là đường thẳng cần dựng.
Vì sao các cách dựng trên cho ta đường phân giác, đường trung trực và đường thẳng vuông góc cần dựng?
Phương pháp giải:
+ Chứng minh cách dựng đường phân giác: Chứng minh \(\Delta BOC = \Delta AOC\left( {c.c.c} \right)\), suy ra \(\widehat {BOC} = \widehat {AOC}\) nên OC là tia phân giác của góc xOy.
+ Chứng minh đường trung trực: Chứng minh \(MA = MB,NA = NB\) nên M, N thuộc đường trung trực của AB, do đó, MN là đường trung trực của AB.
+ Chứng minh đường thẳng vuông góc: Chứng minh \(AB = AC,BD = DC\) nên A, D thuộc đường trung trực của BC. Do đó, AD là đường trung trực của BC nên AD vuông góc với BC.
Lời giải chi tiết:
+ Chứng minh cách dựng đường phân giác:
Vì B, A thuộc (O) nên \(OA = OB\).
Vì đường tròn tâm A và B có cùng bán kính và cắt nhau tại C nên \(CB = CA\).
\(\Delta \)BOC và \(\Delta \)AOC có: \(OA = OB\), \(CB = CA\), OC chung nên \(\Delta BOC = \Delta AOC\left( {c.c.c} \right)\), do đó, \(\widehat {BOC} = \widehat {AOC}\) nên OC là tia phân giác của góc xOy.
+ Chứng minh đường trung trực: Vì hai đường tròn tâm A và tâm B có cùng bán kính và cắt nhau tại M và N nên \(MA = MB,NA = NB\). Do đó, hai điểm M, N thuộc đường trung trực của AB, do đó, MN là đường trung trực của AB.
+ Chứng minh đường thẳng vuông góc:
Vì B, C thuộc (A) nên \(AB = AC\), suy ra A thuộc đường trung trực của BC.
Vì hai đường tròn tâm B và C có cùng bán kính cắt nhau tại điểm D khác A nên \(BD = DC\), suy ra D thuộc đường trung trực của BC.
Vậy AD là đường trung trực của BC. Do đó, đường thẳng AD vuông góc với BC.
Trả lời câu hỏi Thực hành 1 trang 131 SGK Toán 9 Cùng khám phá
Em hãy tìm thêm các hình ảnh về các chi tiết được chắp nối trơn trên thực tế.
Phương pháp giải:
Trong thiết kế và đồ họa, có các chi tiết được chắp nối với nhau bằng các cung của đường tròn. Các đường tròn này thường tiếp xúc với các chi tiết được nối với chúng sao cho đường đi không bị “gãy” mà được trơn tại điểm nối. Khi đó, ta nói các chi tiết được ghép trơn với nhau.
Lời giải chi tiết:
+ Đường vòng xuyến:

+ Xích xe với hai bánh xe:
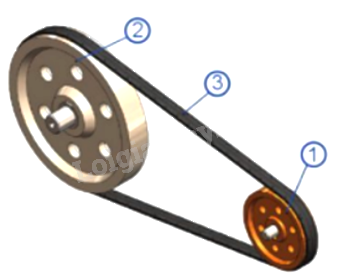
+ Vòi nước:

Trả lời câu hỏi Câu hỏi 1 trang 131SGK Toán 9 Cùng khám phá
Vẽ chắp nối trơn hai tia Ox và Oy tại điểm A thuộc Ox:
Bước 1: Dựng đường phân giác Oz của góc xOy và đường thẳng qua A vuông góc với Ox. Hai đường thẳng cắt nhau tại M.
Bước 2: Dựng đường thẳng qua M vuông góc với Oy cắt tia Oy tại B. Vẽ đường tròn tâm M đi qua A ta được cung AB nối trơn với hai tia Ox và Oy.
Vì sao với cách dựng như trên thì đường tròn (M; MA) tiếp xúc với cả hai tia Ox và Oy?
Phương pháp giải:
+ Vì \(MA \bot Ox\) tại A nên đường tròn (M; MA) tiếp xúc với tia Ox tại A.
+ Chứng minh \(\Delta MOA = \Delta MOB\left( {ch - gn} \right)\) nên \(MA = MB\) nên B thuộc đường tròn (M; MA).
+ Vì \(MB \bot Oy\) tại B nên đường tròn (M; MA) tiếp xúc với tia Oy tại B.
Lời giải chi tiết:
Vì \(MA \bot Ox\) tại A nên đường tròn (M; MA) tiếp xúc với tia Ox tại A.
Vì Oz là tia phân giác góc xOy nên \(\widehat {yOz} = \widehat {zOx}\).
Tam giác MOA và tam giác MOB có: \(\widehat {MBO} = \widehat {MAO} = {90^o},\widehat {BOM} = \widehat {MOA},OM\;chung\).
Do đó, \(\Delta MOA = \Delta MOB\left( {ch - gn} \right)\) nên \(MA = MB\) nên B thuộc đường tròn (M; MA).
Vì \(MB \bot Oy\) tại B nên đường tròn (M; MA) tiếp xúc với tia Oy tại B.
Trả lời câu hỏi Thực hành 2 trang 132SGK Toán 9 Cùng khám phá
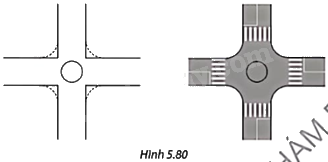
Sử dụng phương pháp nối trơn hai đường thẳng để hoàn thiện phác thảo bên trái và trang trí thành bản vẽ thiết kế ngã tư đường như trong Hình 5.80
Phương pháp giải:
Trong thiết kế và đồ họa, có các chi tiết được chắp nối với nhau bằng các cung của đường tròn. Các đường tròn này thường tiếp xúc với các chi tiết được nối với chúng sao cho đường đi không bị “gãy” mà được trơn tại điểm nối. Khi đó, ta nói các chi tiết được ghép trơn với nhau.
Lời giải chi tiết:
+ Sử dụng phương pháp nối trơn hai đường thẳng, ta vẽ được:
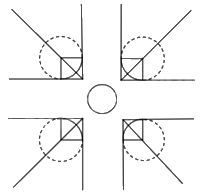
Tiến hành trang trí ta được:

Trả lời câu hỏi Câu hỏi trang 132SGK Toán 9 Cùng khám phá
Nối trơn đường thẳng xy và đường tròn (O) tại điểm A thuộc (O).
Bước 1: Vẽ tiếp tuyến của đường tròn (O) tại A, cắt xy tại điểm M.
Bước 2: Nối trơn tiếp tuyến Mz và tia My tại điểm A theo các bước ở Hoạt động 2, ta được đường nối cần dựng.
Vì sao với cách dựng như trên thì đường tròn (I; IA) tiếp xúc với đường tròn (O) và đường thẳng xy? Trong trường hợp nào hai đường tròn (O) và (I) tiếp xúc ngoài, trong trường hợp nào hai đường tròn tiếp xúc trong?
Phương pháp giải:
+ Theo cách vẽ nối trơn ở hoạt động 2 thì (I; IA) tiếp xúc với My, do đó, (I; IA) tiếp xúc với đường thẳng xy.
+ Vì Mz tiếp xúc với đường tròn (I; IA) tại A, và Mz tiếp xúc với đường tròn (O) tại A nên đường tròn (I; IA) tiếp xúc với đường tròn (O).
+ Nếu \(OA + AI = OI\) nên đường tròn (I; IA) tiếp xúc ngoài với đường tròn (O).
+ Nếu \(\left| {OA - AI} \right| = OI\) nên đường tròn (I; IA) tiếp xúc trong với đường tròn (O).
Lời giải chi tiết:
Vì (I; IA) tiếp xúc với My, do đó, (I; IA) tiếp xúc với đường thẳng xy.
Vì Mz tiếp xúc với đường tròn (I; IA) tại A, và Mz tiếp xúc với đường tròn (O) tại A nên đường tròn (I; IA) tiếp xúc với đường tròn (O).
Nếu \(OA + AI = OI\) nên đường tròn (I; IA) tiếp xúc ngoài với đường tròn (O).
Nếu \(\left| {OA - AI} \right| = OI\) nên đường tròn (I; IA) tiếp xúc trong với đường tròn (O).
Trả lời câu hỏi Thực hành 3 trang 133SGK Toán 9 Cùng khám phá
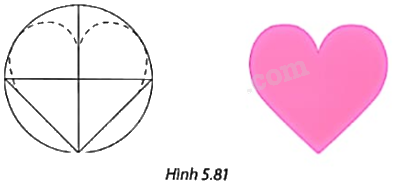
Sử dụng phương pháp nối trơn đường thẳng với đường tròn để hoàn thiện phác thảo bên trái và tô màu thành hoa văn hình trái tim như trong Hình 5.81.
Phương pháp giải:
Sử dụng phương pháp nối trơn đường thẳng với đường tròn.
Lời giải chi tiết:
+ Sử dụng phương pháp nối trơn đường thẳng với đường tròn ta phác thảo được hình trái tim:
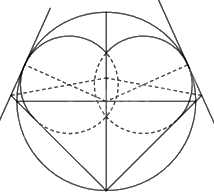
Hoàn thiện hình vẽ ta được:

Trả lời câu hỏi Câu hỏi 2 trang 133 SGK Toán 9 Cùng khám phá
Nối trơn hai đường tròn (O) và (I) từ điểm A thuộc (O).
Bước 1: Xác định điểm J trên bán kính OA sao cho AJ bằng bán kính của (I).
Bước 2: Dựng đường trung trực của IJ cắt đường thẳng OA tại M.
Bước 3: Xác định giao điểm B của MI và đường tròn (I). Vẽ đường tròn tâm M đi qua A, ta được cung AB là đường nối trơn cần dựng.
Vì sao với cách dựng như trên thì \(MA = MB\) và đường tròn (M; MA) tiếp xúc với cả hai đường tròn (O) và (I)?
Phương pháp giải:
+ Chứng minh \(MI = MJ\), \(AJ = BI\), do đó \(MJ - AJ = MI - BI\), nên \(MA = MB\).
+ Vì \(MO = AM + AO\) nên đường tròn (M; MA) tiếp xúc với đường tròn (O).
+ Vì \(MB + BI = MI\) nên đường tròn (M; MA) tiếp xúc với đường tròn (I).
Lời giải chi tiết:
Vì M thuộc đường trung trực của IJ nên \(MI = MJ\).
Vì AJ bằng bán kính (I) mà B thuộc (I) nên \(AJ = BI\).
Do đó, \(MJ - AJ = MI - BI\), nên \(MA = MB\).
Vì \(MO = AM + AO\) nên đường tròn (M; MA) tiếp xúc với đường tròn (O).
Vì \(MB + BI = MI\) nên đường tròn (M; MA) tiếp xúc với đường tròn (I).
Trả lời câu hỏi Thực hành 4 trang 133 SGK Toán 9 Cùng khám phá
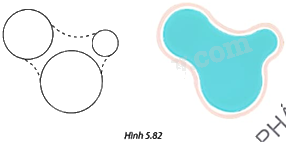
Sử dụng phương pháp nối trơn đường tròn với đường tròn ở trên để hoàn thiện phác thảo bên trái và trang trí thành thiết kế hồ bơi trong Hình 5.82.
Phương pháp giải:
Sử dụng phương pháp nối trơn đường tròn với đường tròn để hoàn thiện bảng phác thảo.
Lời giải chi tiết:
Sử dụng phương pháp nối trơn đường tròn với đường tròn ta được các đường nét trơn (màu xanh):
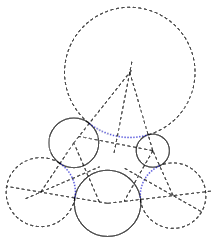
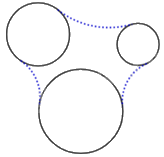
Hoàn thiện hình vẽ ta được:

Trả lời câu hỏi Thực hành 5 trang 134 SGK Toán 9 Cùng khám phá
Sử dụng các phương pháp dựng hình và chắp nối trơn như trên để thực hiện một thiết kế hoặc mẫu hoa văn trang trí tùy ý. Trình bày ý tưởng và mẫu thiết kế trước lớp.
Phương pháp giải:
Sử dụng các phương pháp chắp nối trơn đã nêu ở trên để vẽ.
Lời giải chi tiết:
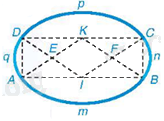
Cách vẽ hình “trái xoan”
+ Vẽ hình chữ nhật ABCD.
+ Xác định trung điểm I của đoạn thẳng AB và trung điểm K của đoạn thẳng CD.
+ Tìm giao điểm E của AK và DI; giao điểm F của BK và CI.
+ Vẽ 4 cung: Cung AmB (tâm K), cung CpD (tâm I), cung BnC (tâm F), cung DqA (tâm E).
Khi đó, bốn cung tròn vừa vẽ tạo nên hình “trái xoan”. Trong đó, tâm hai cung liên tiếp, chẳng hạn tâm K của cung AmB và tâm F của cung BnC thẳng hàng với điểm nối trơn B, chứng tỏ hai đường tròn (K) và (F) tiếp xúc nhau tại B. Khi đó, hai cung này nối trơn với nhau tại B.
Chứng minh tương tự với các cặp cung còn lại.
Chương trình Toán 9 tập 1 tập trung vào việc củng cố và mở rộng kiến thức về hàm số bậc nhất, hàm số bậc hai, hệ phương trình bậc hai và ứng dụng của chúng vào giải quyết các bài toán thực tế. Trang 130, 131 và 132 của SGK Toán 9 tập 1 chứa các bài tập vận dụng kiến thức đã học để giải quyết các bài toán liên quan đến hàm số và phương trình.
Các bài tập trên trang 130 thường tập trung vào việc xác định hệ số góc và tung độ gốc của đường thẳng, viết phương trình đường thẳng khi biết các yếu tố khác nhau, và xác định giao điểm của hai đường thẳng. Để giải các bài tập này, học sinh cần nắm vững các khái niệm về hàm số bậc nhất và phương trình đường thẳng.
Trang 131 tiếp tục củng cố kiến thức về hàm số bậc nhất và phương trình đường thẳng, đồng thời giới thiệu các bài tập liên quan đến ứng dụng của hàm số vào giải quyết các bài toán thực tế. Các bài tập này thường yêu cầu học sinh vẽ đồ thị hàm số, xác định khoảng giá trị của hàm số, và giải các bài toán về tốc độ, quãng đường, thời gian.
Các bài tập trên trang 132 thường tập trung vào việc giải hệ phương trình bậc hai và ứng dụng của hệ phương trình vào giải quyết các bài toán thực tế. Để giải các bài tập này, học sinh cần nắm vững các phương pháp giải hệ phương trình bậc hai, như phương pháp thế, phương pháp cộng đại số, và phương pháp đặt ẩn phụ.
Ví dụ: Giải hệ phương trình sau:
| x | y | |
|---|---|---|
| Phương trình 1 | 2x + y = 5 | |
| Phương trình 2 | x - y = 1 |
Lời giải: Cộng hai phương trình, ta được: 3x = 6 => x = 2. Thay x = 2 vào phương trình 2, ta được: 2 - y = 1 => y = 1. Vậy nghiệm của hệ phương trình là (x, y) = (2, 1).
Giaitoan.edu.vn cung cấp đầy đủ lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong SGK Toán 9 tập 1. Chúng tôi cũng cung cấp các bài giảng video, bài tập trắc nghiệm và các tài liệu học tập khác để giúp các em học toán hiệu quả hơn. Hãy truy cập giaitoan.edu.vn để được hỗ trợ tốt nhất!