Chào mừng bạn đến với bài học về lý thuyết Tần số ghép nhóm và tần số tương đối ghép nhóm trong chương trình Toán 9. Đây là một phần kiến thức quan trọng trong thống kê, giúp chúng ta phân tích và hiểu rõ hơn về dữ liệu.
Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản nhất về khái niệm, công thức và cách áp dụng của hai khái niệm này vào giải các bài tập thực tế.
1. Mẫu số liệu ghép nhóm. Tần số ghép nhóm Mẫu số liệu ghép nhóm là một mẫu mà các số liệu đã được ghép với nhau thành từng nhóm, theo một tiêu chí xác định. Các nhóm thường có dạng [a; b), hoặc (a; b], hoặc [a; b]. Hai số a, b được gọi là các mút của nhóm. Nhóm [a; b) (tương ứng: (a; b] hoặc [a; b]) gồm những giá trị x thoả mãn điều kiện a ≤ x < b (tương ứng: a < x < b hoặc a ≤ x < b). Số lần xuất hiện các giá trị thuộc một nhóm được gọi là tần số ghép nhóm của nhóm đó. Mẫu số liệu ghép nhó
1. Mẫu số liệu ghép nhóm. Tần số ghép nhóm
Mẫu số liệu ghép nhóm là một mẫu mà các số liệu đã được ghép với nhau thành từng nhóm, theo một tiêu chí xác định. Các nhóm thường có dạng [a; b), hoặc (a; b], hoặc [a; b]. Hai số a, b được gọi là các mút của nhóm. Nhóm [a; b) (tương ứng: (a; b] hoặc [a; b]) gồm những giá trị x thoả mãn điều kiện a ≤ x < b (tương ứng: a < x < b hoặc a ≤ x < b). Số lần xuất hiện các giá trị thuộc một nhóm được gọi là tần số ghép nhóm của nhóm đó. Mẫu số liệu ghép nhóm có thể được biểu diễn bởi một bảng gồm hai dòng (cột). Dòng (cột) thứ nhất dành cho việc viết các nhóm. Dòng (cột) thứ hai ghi tần số của nhóm tương ứng. Bảng này được gọi là bảng tần số ghép nhóm. |
Chú ý: Bảng tần số ghép nhóm ở dạng bảng dọc được lập bằng cách tương tự như trên.
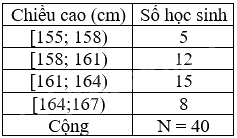
Ví dụ: Ta có bảng tần số ghép nhóm cho mẫu số liệu chiều cao (đơn vị là cm) của học sinh lớp 9A với các nhóm [155; 158), [158; 161), [161; 164), [164;167) ở dạng bảng ngang:

hoặc ở dạng bảng dọc:
Nhận xét:
Việc ghép nhóm số liệu giúp ta trình bày mẫu số liệu được gọn gàng, nhất là với các dãy số liệu liên tục, có nhiều giá trị mà sự phân biệt các giá trị gần bằng nhau lại không cần thiết. Lúc quan sát mẫu số liệu ghép nhóm, thông tin về tần số của mỗi nhóm là yếu tố quan trọng.
Lưu ý:
Trong nhiều bảng thống kê trên báo chí hoặc Internet, ta có thể gặp cách ghi các nhóm ghép bằng bất đẳng thức.
Ví dụ:

Các nhóm (146; 152), [164; 170] trong bảng trên có thể được viết là 146 ≤ h < 152, 164 ≤ h ≤ 170 (với h là chiều cao).
2. Tần số tương đối ghép nhóm
Nếu mẫu số liệu gồm k nhóm (k là một số nguyên dương) và \({n_1},{n_2},...,{n_k}\) là tần số của các nhóm thì tỉ số \({f_i} = \frac{{{n_i}}}{N},i = 1,2,...,k\) trong đó N là kích thước mẫu, được gọi là tần số tương đối của nhóm thứ i. Mẫu số liệu ghép nhóm có thể được biểu diễn bởi một bảng gồm hai dòng (cột), trong đó: • Dòng (cột) thứ nhất viết các nhóm; • Dòng (cột) thứ hai viết tần số tương đối của nhóm tương ứng. Người ta gọi đó là bảng tần số tương đối ghép nhóm. |
Một bảng có cả tần số ghép nhóm và tần số tương đối ghép tần số được gọi là bảng tần số - tần số tương đối ghép nhóm.
3. Biểu đồ tần số tương đối ghép nhóm dạng cột
Để mô tả các bảng tần số tương đối ghép nhóm, ta có thể dùng biểu đồ tần số tương đối ghép nhóm dạng cột (histogram).
Cách vẽ:
- Vẽ hệ trục tọa độ Oxy; - Trên trục Ox, đánh dấu hai đầu mút của từng nhóm, từ đó xác định được các đoạn ứng với các nhóm. - Tại mỗi đoạn thẳng, dựng một hình chữ nhật có chiều cao biểu diễn tần số tương đối của nhóm tương ứng. |
4. Biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ đoạn thẳng
Cách vẽ
- Vẽ hệ trục tọa độ Oxy. Trên trục Ox, đánh dấu hai đầu mút của từng nhóm, từ đó xác định được các đoạn ứng với các nhóm. - Lấy các điểm \(\left( {{c_i};{f_i}} \right),i = 1,...,n\), trong đó \({c_i}\) là trung bình cộng hai đầu mút của nhóm thứ \(i\) và \({f_i}\) là tần số tương đối của nhóm đó. \({c_i}\) là các giá trị đại diện của nhóm thứ i. - Vẽ các đoạn thẳng nối hai điểm \(\left( {{c_i};{f_i}} \right)\) và \(\left( {{c_{i + 1}};{f_{i + 1}}} \right)\) với \(i = 1,2,3,...,n\); ta thu được biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng biểu diễn dữ liệu. |
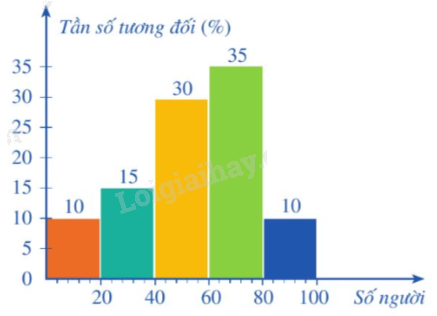
Ví dụ: Bảng tần số tương đối ghép nhóm của mẫu số liệu thống kê số lượng người đến đọc sách trong 100 ngày liên tiếp của một thư viện.

Biểu đồ tần số tương đối ghép nhóm dạng cột của bảng tần số tương đối trên là:
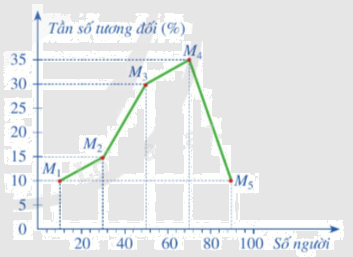
Biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng của bảng tần số tương đối trên là:
Trong chương trình Toán 9, việc làm quen với các khái niệm thống kê cơ bản là vô cùng quan trọng. Tần số ghép nhóm và tần số tương đối ghép nhóm là hai khái niệm then chốt giúp học sinh phân tích và tóm tắt dữ liệu một cách hiệu quả. Bài viết này sẽ đi sâu vào lý thuyết, công thức và các ví dụ minh họa để bạn có thể nắm vững kiến thức này.
Tần số ghép nhóm là số lần xuất hiện của một giá trị hoặc một khoảng giá trị trong một tập dữ liệu. Để hiểu rõ hơn, chúng ta hãy xem xét một ví dụ:
Giả sử chúng ta có một bảng thống kê điểm kiểm tra Toán của 20 học sinh:
| Điểm | Số Học Sinh |
|---|---|
| 5 | 2 |
| 6 | 3 |
| 7 | 5 |
| 8 | 4 |
| 9 | 6 |
Trong bảng này, tần số ghép nhóm của điểm 7 là 5, nghĩa là có 5 học sinh đạt điểm 7.
Tần số tương đối ghép nhóm là tỷ lệ phần trăm của tần số ghép nhóm so với tổng số các giá trị trong tập dữ liệu. Công thức tính tần số tương đối ghép nhóm như sau:
Tần số tương đối ghép nhóm = (Tần số ghép nhóm / Tổng số các giá trị) * 100%
Sử dụng bảng dữ liệu điểm kiểm tra Toán ở trên, chúng ta có thể tính tần số tương đối ghép nhóm của điểm 7 như sau:
Tần số tương đối ghép nhóm của điểm 7 = (5 / 20) * 100% = 25%
Điều này có nghĩa là 25% số học sinh đạt điểm 7.
Việc ghép nhóm dữ liệu là bước quan trọng để tạo ra bảng tần số ghép nhóm. Dưới đây là một số phương pháp ghép nhóm dữ liệu phổ biến:
Tần số ghép nhóm và tần số tương đối ghép nhóm có rất nhiều ứng dụng trong thực tế, bao gồm:
Bài tập 1: Một cửa hàng bán được các số lượng áo sơ mi như sau trong một tuần:
Thứ Hai: 20 chiếc, Thứ Ba: 25 chiếc, Thứ Tư: 18 chiếc, Thứ Năm: 30 chiếc, Thứ Sáu: 22 chiếc, Thứ Bảy: 35 chiếc, Chủ Nhật: 40 chiếc.
Hãy lập bảng tần số ghép nhóm và tính tần số tương đối ghép nhóm cho mỗi ngày.
Bài tập 2: Một lớp học có 30 học sinh. Kết quả kiểm tra môn Toán của các em như sau:
5, 6, 7, 8, 9, 6, 7, 8, 5, 7, 9, 8, 6, 7, 8, 9, 5, 6, 7, 8, 9, 6, 7, 8, 5, 6, 7, 8, 9, 7.
Hãy lập bảng tần số ghép nhóm và tính tần số tương đối ghép nhóm cho mỗi điểm.
Lý thuyết Tần số ghép nhóm và tần số tương đối ghép nhóm là những công cụ hữu ích để phân tích và tóm tắt dữ liệu. Việc nắm vững kiến thức này sẽ giúp bạn giải quyết các bài toán thống kê một cách dễ dàng và hiệu quả. Hy vọng bài viết này đã cung cấp cho bạn những thông tin hữu ích và giúp bạn hiểu rõ hơn về chủ đề này.