Chào mừng các em học sinh đến với bài giải bài tập 5.12 trang 110 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
Trên mặt phẳng tọa độ Oxy, cho điểm M(2; 5). Xác định: a) Vị trí tương đối của đường tròn tâm M, bán kính 3 với hai trục Ox và Oy; b) Bán kính của đường tròn tâm M tiếp xúc với trục Ox.
Đề bài
Trên mặt phẳng tọa độ Oxy, cho điểm M(2; 5). Xác định:
a) Vị trí tương đối của đường tròn tâm M, bán kính 3 với hai trục Ox và Oy;
b) Bán kính của đường tròn tâm M tiếp xúc với trục Ox.
Phương pháp giải - Xem chi tiết
Cho đường tròn (O; R) và đường thẳng a. Đặt d là khoảng cách từ O đến đường thẳng a. Vị trí tương đối của đường thẳng a và đường tròn (O; R) có thể được xác định dựa vào mối quan hệ giữa R và d như sau:
+ Nếu \(d > R\) thì đường thẳng a và đường tròn (O) không giao nhau.
+ Nếu \(d = R\) thì đường thẳng a và đường tròn (O) tiếp xúc nhau.
+ Nếu \(d < R\) thì đường thẳng a và đường tròn (O) cắt nhau.
Lời giải chi tiết
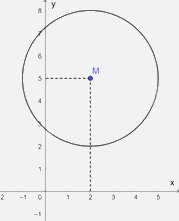
a) Khoảng cách từ M đến trục Oy bằng 2. Vì \(2 < 3\) nên đường tròn tâm M, bán kính 3 cắt trục Oy.
Khoảng cách từ M đến trục Ox bằng 5. Vì \(5 > 3\) nên đường tròn tâm M, bán kính 3 và trục Ox không giao nhau.
b) Để đường tròn tâm M tiếp xúc với trục Ox thì bán kính đường tròn tâm M bằng khoảng cách từ M đến trục Ox. Do đó, bán kính đường tròn tâm M bằng 5.
Bài tập 5.12 trang 110 SGK Toán 9 tập 1 yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết một bài toán thực tế liên quan đến việc xác định phương trình đường thẳng và ứng dụng của nó trong việc tìm điểm giao nhau của các đường thẳng.
Bài tập 5.12 thường có dạng như sau: Cho một hàm số y = ax + b. Hãy tìm giá trị của a và b sao cho đường thẳng biểu diễn hàm số đi qua hai điểm cho trước hoặc thỏa mãn một điều kiện nào đó.
Bài tập: Tìm giá trị của a và b sao cho đường thẳng y = ax + b đi qua hai điểm A(1; 2) và B(-1; 0).
Giải:
Giải hệ phương trình (1) và (2), ta có:
a + b = 2
-a + b = 0
Cộng hai phương trình, ta được: 2b = 2 => b = 1
Thay b = 1 vào phương trình a + b = 2, ta được: a + 1 = 2 => a = 1
Vậy, a = 1 và b = 1. Phương trình đường thẳng cần tìm là y = x + 1.
Ngoài dạng bài tập tìm a và b khi đường thẳng đi qua hai điểm, bài tập 5.12 còn có thể xuất hiện ở các dạng khác như:
Để giải các dạng bài tập này, học sinh cần nắm vững các kiến thức về:
Bài tập 5.12 trang 110 SGK Toán 9 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất và ứng dụng của nó. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh sẽ tự tin giải quyết bài tập này một cách hiệu quả.