Chào mừng các em học sinh đến với bài giải bài tập 9.6 trang 75 SGK Toán 9 tập 2 trên giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán. Đồng thời, chúng tôi cũng cung cấp các bài tập tương tự để các em luyện tập và củng cố kiến thức.
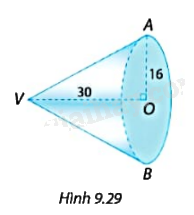
Kể tên đỉnh, chiều cao, đường sinh, bán kính đáy và tính diện tích xung quanh, thể tích của hình nón ở Hình 9.29.
Đề bài
Kể tên đỉnh, chiều cao, đường sinh, bán kính đáy và tính diện tích xung quanh, thể tích của hình nón ở Hình 9.29.
Phương pháp giải - Xem chi tiết
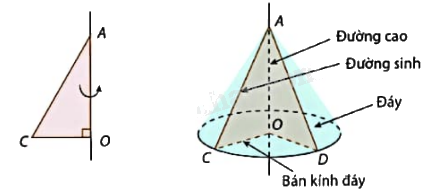
Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rn\) (với r là bán kính đáy và n là đường sinh của hình nón).
Thể tích hình nón: \(V = \frac{1}{3}\pi {r^2}h\) (với r là bán kính đáy và h là chiều cao của hình nón).
Lời giải chi tiết
Đỉnh V, chiều cao VO, đường sinh VA, bán kính đáy OA.
Đường sinh VA là:
\(\sqrt {{{30}^2} + {{16}^2}} = 34\)
Diện tích xung quanh của hình nón là:
\({S_{xq}} = \pi rn = \pi .16.34 = 544\pi \)(đvdđ)
Thể tích hình nón là:
\(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.16^2}.30 = 2560\pi \) (đvtt).
Bài tập 9.6 trang 75 SGK Toán 9 tập 2 yêu cầu chúng ta xét dấu của hàm số bậc nhất y = ax + b (a ≠ 0). Việc xét dấu hàm số là một kỹ năng quan trọng trong toán học, giúp chúng ta hiểu rõ hơn về tính chất của hàm số và ứng dụng vào giải quyết các bài toán thực tế.
Trước khi đi vào giải bài tập, chúng ta cần nắm vững các kiến thức sau:
Bài tập 9.6 thường yêu cầu xét dấu của một hàm số bậc nhất cụ thể. Để giải bài tập này, chúng ta cần thực hiện các bước sau:
Giả sử bài tập 9.6 yêu cầu xét dấu hàm số y = 2x - 4.
Vậy, hàm số y = 2x - 4 âm khi x < 2, bằng 0 khi x = 2 và dương khi x > 2.
Ngoài bài tập 9.6, còn rất nhiều bài tập tương tự yêu cầu xét dấu hàm số bậc nhất. Để giải các bài tập này, chúng ta cần áp dụng các bước tương tự như đã trình bày ở trên. Tuy nhiên, cần lưu ý rằng hệ số a và nghiệm của hàm số có thể khác nhau, do đó chúng ta cần cẩn thận trong quá trình giải.
Để củng cố kiến thức và kỹ năng giải bài tập về xét dấu hàm số bậc nhất, các em có thể tự giải các bài tập sau:
Bài tập 9.6 trang 75 SGK Toán 9 tập 2 là một bài tập quan trọng giúp các em hiểu rõ hơn về tính chất của hàm số bậc nhất và ứng dụng vào giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em sẽ nắm vững kiến thức và kỹ năng giải bài tập này một cách hiệu quả.
Chúc các em học tập tốt!