Chào mừng bạn đến với chuyên mục Lý thuyết Bất đẳng thức Toán 9 tại giaitoan.edu.vn. Bất đẳng thức là một phần quan trọng trong chương trình Toán học lớp 9, giúp học sinh rèn luyện tư duy logic và kỹ năng giải quyết vấn đề.
Chúng tôi cung cấp đầy đủ các kiến thức cơ bản, các định nghĩa, tính chất và các dạng bài tập thường gặp về bất đẳng thức, giúp bạn nắm vững lý thuyết và tự tin giải các bài toán thực tế.
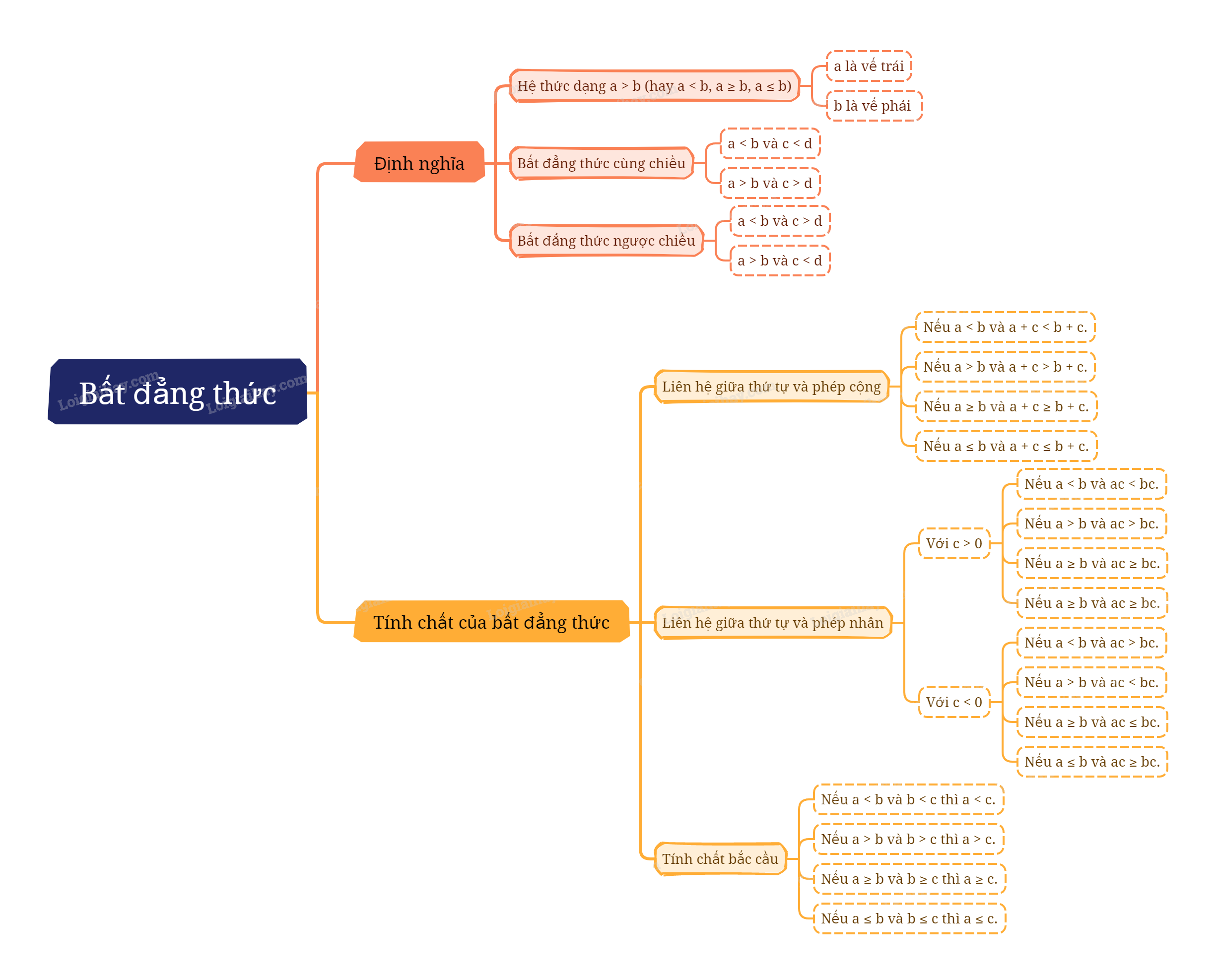
1. Bất đẳng thức Khi so sánh hai số thực a, b bất kì, luôn xảy ra một trong ba trường hợp sau:
1. Bất đẳng thức
Khi so sánh hai số thực a, b bất kì, luôn xảy ra một trong ba trường hợp sau:
- Số a bằng số b, kí hiệu \(a = b\);
- Số a lớn hơn số b, kí hiệu \(a > b\);
- Số a nhỏ hơn số b, kí hiệu \(a < b\).
Nếu số a không lớn hơn số b thì phải có hoặc \(a < b\), hoặc \(a = b\). Khi đó ta nói gọn là a nhỏ hơn hoặc bằng b và kí hiệu \(a \le b\).
Nếu số a không nhỏ hơn số b thì ta phải có hoặc \(a > b\), hoặc \(a = b\). Khi đó, ta nói a lớn hơn hoặc bằng b và kí hiệu \(a \ge b\).
Định nghĩa bất đẳng thức
Hệ thức dạng \(a > b\) (hay \(a < b\), \(a \ge b\), \(a \le b\)) được gọi là bất đẳng thức. Khi đó a được gọi là vế trái và b được gọi là vế phải của bất đẳng thức. |
Lưu ý:
Bất đẳng thức a > b còn được viết là b < a.
Nếu đồng thời có hai bất đẳng thức a > b và a < c thì ta viết gộp lại thành b < a < c (đọc là a lớn hơn b, nhỏ hơn c)
Hai bất đẳng thức \(a > b\) và \(c > d\) (hay \(a \ge b\) và \(c \ge d\)) được gọi là hai bất đẳng thức cùng chiều.
Hai bất đẳng thức \(a > b\) và \(c < d\) (hay \(a \ge b\) và \(c \le d\)) được gọi là hai bất đẳng thức ngược chiều.
2. Liên hệ giữa thứ tự và phép cộng
Với ba số a, b, c, ta có:
Nếu \(a < b\) thì \(a + c < b + c\). Nếu \(a > b\) thì \(a + c > b + c\). Nếu \(a \le b\) thì \(a + c \le b + c\). Nếu \(a \ge b\) thì \(a + c \ge b + c\). Khi cộng cùng một số vào hai vế của bất đẳng thức, ta được bất đẳng thức mới cùng chiều với bất đẳng thức ban đầu. |
Ví dụ:Vì \(2023 < 2024\) nên \(2023 + \left( { - 19} \right) < 2024 + \left( { - 19} \right)\)
Lưu ý:
Tính chất trên vẫn đúng khi ta trừ vào hai vế của bất đẳng thức với cùng một số. Chẳng hạn, nếu \(a < b\) thì \(a - c < b - c\).
Ta có thể sử dụng tính chất trên để so sánh hai số hoặc chứng minh một bất đẳng thức.
3. Liên hệ giữa thứ tự và phép nhân
a) Liên hệ giữa thứ tự và phép nhân với số dương
Với ba số a, b, c bất kì, trong đó c > 0, ta có: - Nếu \(a < b\) thì \(ac < bc\). - Nếu \(a > b\) thì \(ac > bc\). - Nếu \(a \le b\) thì \(ac \le bc\). - Nếu \(a \ge b\) thì \(ac \ge bc\). Khi nhân cả hai vế của một bất đẳng thức với cùng một số dương, ta được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho. |
Lưu ý:
Tính chất trên vẫn đúng khi ta chia hai vế của bất đẳng thức cho cùng một số dương.
Chẳng hạn, nếu \(a < b\) thì \(\frac{a}{c} < \frac{b}{c}\) với c là số dương bất kì.
b) Liên hệ giữa thứ tự và phép nhân với số âm
Với ba số a, b, c, trong đó c < 0, ta có: Nếu \(a < b\) thì \(ac > bc\). Nếu \(a > b\) thì \(ac < bc\). Nếu \(a \le b\) thì \(ac \ge bc\). Nếu \(a \ge b\) thì \(ac \le bc\). Khi nhân cả hai vế của một bất đẳng thức với cùng một số âm ta được bất đẳng thức mới ngược chiều với bất đẳng thức đã cho. |
Lưu ý:
Tính chất trên vẫn đúng khi ta chia hai vế của bất đẳng thức cho cùng một số âm.
Chẳng hạn, nếu \(a < b\) thì \(\frac{a}{c} > \frac{b}{c}\) với c là số âm bất kì.
Ví dụ:
Vì \( - 7 < - 5\) và \(3 > 0\) nên \(3.\left( { - 7} \right) < 3.\left( { - 5} \right)\).
Vì \( - 7 < - 5\) và \( - 3 < 0\) nên \(\left( { - 3} \right).\left( { - 7} \right) > \left( { - 3} \right).\left( { - 5} \right)\).
4. Tính chất bắc cầu của thứ tự
Nếu \(a < b\) và \(b < c\) thì \(a < c\). Tính chất này gọi là tính chất bắc cầu của thứ tự. |
Tính chất bắc cầu cũng đúng với các thứ tự lớn hơn (>), lớn hơn hoặc bằng (\( \ge \)), nhỏ hơn hoặc bằng (\( \le \)).
Ví dụ: Vì \(\frac{{2024}}{{2023}} = 1 + \frac{1}{{2023}} > 1\) và \(\frac{{2021}}{{2022}} = 1 - \frac{1}{{2022}} < 1\) nên \(\frac{{2024}}{{2023}} > \frac{{2021}}{{2022}}\).
Lưu ý:
Các tính chất của thứ tự cũng chính là tính chất của bất đẳng thức.
Bất đẳng thức là một biểu thức toán học so sánh hai giá trị, sử dụng các ký hiệu >, <, ≥, ≤. Trong chương trình Toán 9, học sinh sẽ được làm quen với các loại bất đẳng thức cơ bản, các tính chất của bất đẳng thức và các phương pháp giải bất đẳng thức.
Việc giải bất đẳng thức đòi hỏi học sinh phải nắm vững các tính chất của bất đẳng thức và áp dụng một cách linh hoạt. Một số phương pháp giải bất đẳng thức thường được sử dụng:
Ví dụ 1: Giải bất đẳng thức 2x + 3 > 5
Giải:
Vậy nghiệm của bất đẳng thức là x > 1.
Ví dụ 2: Giải bất đẳng thức (x - 1)(x + 2) < 0
Giải:
Xét dấu (x - 1)(x + 2):
| x | -2 | 1 |
|---|---|---|
| x - 1 | - | + |
| x + 2 | - | + |
| (x - 1)(x + 2) | + | - |
Vậy nghiệm của bất đẳng thức là -2 < x < 1.
Để củng cố kiến thức về lý thuyết bất đẳng thức, bạn có thể thực hành giải các bài tập sau:
Lý thuyết Bất đẳng thức Toán 9 là một phần quan trọng trong chương trình học. Việc nắm vững lý thuyết và các phương pháp giải bất đẳng thức sẽ giúp bạn tự tin giải các bài toán và đạt kết quả tốt trong các kỳ thi.