Chào mừng các em học sinh đến với bài giải bài tập 4.8 trang 86 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương Hàm số bậc nhất và là một phần quan trọng trong việc củng cố kiến thức về hàm số.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin làm bài tập.
Hãy cùng khám phá lời giải ngay dưới đây!
Tính độ dài cạnh x, y và số đo góc \(\alpha \) trong mỗi trường hợp ở Hình 4.23.
Đề bài
Tính độ dài cạnh x, y và số đo góc \(\alpha \) trong mỗi trường hợp ở Hình 4.23.
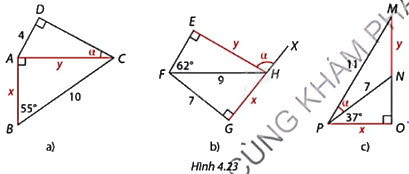
Phương pháp giải - Xem chi tiết
Hình a: \(\Delta \)ABC vuông tại A nên \(y = BC.\sin B;x = BC.\cos B\)
\(\Delta \)ADC vuông tại D nên \(\sin \alpha = \frac{{AD}}{{AC}}\) nên tính được \(\alpha \).
Hình b:
+ \(\Delta \)GFH vuông tại F nên \(F{G^2} + G{H^2} = F{H^2}\) nên tính được x
\(\sin GHF = \frac{{FG}}{{FH}} = \frac{7}{9}\) nên tính được góc FHG.
+ \(\Delta \)EFH vuông tại E nên \(y = FH.\sin EFH,\widehat {EHF} = {90^o} - \widehat {EFH}\). Do đó, \(\alpha = {180^o} - \widehat {EHF} - \widehat {FHG}\).
Hình c:
+ \(\Delta \)ONP vuông tại O nên \(x = PN.\cos NPO,NO = PN.\sin NPO\)
+ \(\Delta \)OMP vuông tại O nên \(\cos OPM = \frac{{OP}}{{PM}}\) nên tính được góc OPM, \(MO = PM.\sin MPO\)
Do đó, \(\alpha = \widehat {OPM} - \widehat {OPN},y = MN = MO - NO\)
Lời giải chi tiết
Hình a:
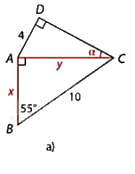
\(\Delta \)ABC vuông tại A nên
\(y = BC.\sin B = 10\sin {55^o} \approx 8,2;x = BC.\cos B = 10\cos {55^o} \approx 5,7\)
Tam giác ADC vuông tại D nên
\(\sin \alpha = \frac{{AD}}{{AC}} = \frac{4}{{8,2}} = \frac{{20}}{{41}}\) nên \(\alpha \approx {29^o}12'\).
Hình b:
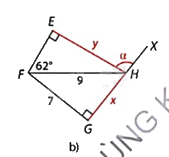
\(\Delta \)GFH vuông tại F nên \(F{G^2} + G{H^2} = F{H^2}\) (định lí Pythagore) nên \(x = GH = \sqrt {F{H^2} - F{G^2}} = \sqrt {{9^2} - {7^2}} = 4\sqrt 2 \approx 5,7\)
\(\sin GHF = \frac{{FG}}{{FH}} = \frac{7}{9}\) nên \(\widehat {FHG} \approx {51^o}3'\)
\(\Delta \)EFH vuông tại E nên
\(y = FH.\sin EFH = 9.\sin {62^o} \approx 7,9\), \(\widehat {EHF} = {90^o} - \widehat {EFH} = {90^o} - {62^o} = {28^o}\).
Do đó, \(\alpha = {180^o} - \widehat {EHF} - \widehat {FHG}\) \( \approx {180^o} - {28^o} - {29^o}11'\) \( \approx {122^o}49'\).
Hình c:
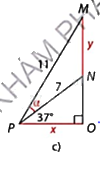
\(\Delta \)ONP vuông tại O nên \(x = PN.\cos NPO = 7.\cos {37^o} \approx 5,6\), \(NO = PN.\sin NPO = 7.\sin {37^o} \approx 4,2\).
\(\Delta \)OMP vuông tại O nên \(\cos OPM = \frac{{OP}}{{PM}} \approx \frac{{5,6}}{{11}}\) nên \(\widehat {OPM} \approx {59^o}24'\),
\(MO = PM.\sin MPO = 11.\sin {59^o}24' \approx 9,5\)
Do đó, \(\alpha = \widehat {OPM} - \widehat {OPN} \approx {22^o}24',y = MN = MO - NO \approx 5,3\)
Bài tập 4.8 trang 86 SGK Toán 9 tập 1 yêu cầu chúng ta xác định hệ số góc của đường thẳng và vẽ đồ thị hàm số. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản về hàm số bậc nhất, bao gồm:
Đề bài yêu cầu chúng ta xác định hệ số góc của đường thẳng và vẽ đồ thị hàm số. Để làm được điều này, chúng ta cần:
a) y = 2x + 1
Hệ số góc của đường thẳng là a = 2.
Để vẽ đồ thị hàm số, ta xác định hai điểm thuộc đồ thị:
Nối hai điểm A(0; 1) và B(1; 3) ta được đồ thị hàm số y = 2x + 1.
b) y = -x + 2
Hệ số góc của đường thẳng là a = -1.
Để vẽ đồ thị hàm số, ta xác định hai điểm thuộc đồ thị:
Nối hai điểm C(0; 2) và D(1; 1) ta được đồ thị hàm số y = -x + 2.
c) y = 0.5x - 3
Hệ số góc của đường thẳng là a = 0.5.
Để vẽ đồ thị hàm số, ta xác định hai điểm thuộc đồ thị:
Nối hai điểm E(0; -3) và F(2; -2) ta được đồ thị hàm số y = 0.5x - 3.
Khi giải các bài tập về hàm số bậc nhất, các em cần lưu ý những điều sau:
Hàm số bậc nhất có rất nhiều ứng dụng trong thực tế, ví dụ như:
Để củng cố kiến thức về hàm số bậc nhất, các em có thể làm thêm các bài tập tương tự sau:
Hy vọng với lời giải chi tiết và những lưu ý trên, các em sẽ hiểu rõ hơn về bài tập 4.8 trang 86 SGK Toán 9 tập 1 và tự tin giải các bài tập tương tự. Chúc các em học tốt!