Chào mừng các em học sinh đến với bài giải bài tập 9.20 trang 86 SGK Toán 9 tập 2 tại giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
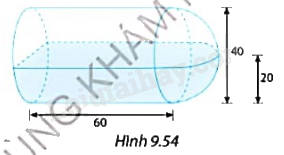
Một bình nước dạng hình trụ kết hợp với nửa hình cầu có kích thước như Hình 9.54. Khi bình nước nằm ngang, mực nước trong bình cao 20 cm. a) Tính thể tích nước trong bình. b) Nếu đặt bình nước thẳng đứng sao cho phần nửa hình cầu ở trên thì chiều cao mực nước trong bình là bao nhiêu?
Đề bài
Một bình nước dạng hình trụ kết hợp với nửa hình cầu có kích thước như Hình 9.54. Khi bình nước nằm ngang, mực nước trong bình cao 20 cm.
a) Tính thể tích nước trong bình.
b) Nếu đặt bình nước thẳng đứng sao cho phần nửa hình cầu ở trên thì chiều cao mực nước trong bình là bao nhiêu?
Phương pháp giải - Xem chi tiết
Thể tích của hình cầu là: \(V = \frac{4}{3}\pi {R^3}\)(với R là bán kính hình cầu)
Diện tích mặt cầu là: S = \(4\pi {R^2}\)
Diện tích hình tròn là: S = \(\pi {R^2}\)
Lời giải chi tiết
a) Thể tích bình là:
\(V = \frac{1}{2}\frac{4}{3}\pi {.20^3} + \pi {.20^2}.60 = \frac{{88000}}{3}\pi \) (cm3)
Vì chiều cao mực nước trong bể bằng nửa chiều cao bể nên thể tích nước trong bình bằng một nửa thể tích bể.
Thể tích nước trong bể là:
\(V = \frac{1}{2}.\frac{{88000}}{3}\pi = \frac{{44000}}{3}\pi \) (cm3)
b) Ta có Vnước < Vtrụ
Suy ra khi dựng thẳng đứng bình thì chiều cao của nước < chiều cao của hình trụ hay Vnước = \(\pi {.20^2}\). hnước = \(\frac{{44000}}{3}\pi \) (cm3)
Suy ra hnước = \(\frac{{44000}}{3}\pi : \left(\pi {.20^2}\right) = \frac{{110}}{3}\) cm.
Bài tập 9.20 trang 86 SGK Toán 9 tập 2 là một bài toán ứng dụng thực tế của hàm số bậc nhất. Để giải bài toán này, chúng ta cần hiểu rõ các khái niệm về hàm số bậc nhất, hệ số góc, và cách xác định đường thẳng trên mặt phẳng tọa độ.
Cho hàm số y = ax + b. Biết rằng hàm số đi qua hai điểm A(0; -2) và B(1; 1).
Bước 1: Xác định hệ số a và b
Vì hàm số y = ax + b đi qua điểm A(0; -2), ta thay x = 0 và y = -2 vào phương trình hàm số, ta được:
-2 = a * 0 + b => b = -2
Vì hàm số y = ax + b đi qua điểm B(1; 1), ta thay x = 1 và y = 1 vào phương trình hàm số, ta được:
1 = a * 1 + b => 1 = a - 2 => a = 3
Vậy, hàm số có dạng y = 3x - 2.
Bước 2: Vẽ đồ thị của hàm số
Để vẽ đồ thị của hàm số y = 3x - 2, ta cần xác định hai điểm thuộc đồ thị. Ta đã có hai điểm A(0; -2) và B(1; 1). Vẽ đường thẳng đi qua hai điểm này, ta được đồ thị của hàm số.
Bước 3: Tính các giá trị của y khi x = -1 và x = 2
Khi x = -1, ta có y = 3 * (-1) - 2 = -3 - 2 = -5
Khi x = 2, ta có y = 3 * 2 - 2 = 6 - 2 = 4
Hàm số bậc nhất có nhiều ứng dụng trong đời sống và khoa học. Ví dụ, trong vật lý, hàm số bậc nhất có thể mô tả mối quan hệ giữa quãng đường đi được và thời gian khi vật chuyển động đều. Trong kinh tế, hàm số bậc nhất có thể mô tả mối quan hệ giữa chi phí sản xuất và số lượng sản phẩm.
Để củng cố kiến thức về hàm số bậc nhất, các em có thể tự giải các bài tập tương tự sau:
Bài tập 9.20 trang 86 SGK Toán 9 tập 2 là một bài tập quan trọng giúp các em hiểu rõ hơn về hàm số bậc nhất và ứng dụng của nó. Hy vọng với lời giải chi tiết và các lưu ý quan trọng trên, các em sẽ tự tin giải bài tập này và các bài tập tương tự một cách hiệu quả.