Chào mừng bạn đến với bài học về lý thuyết hàm số bậc hai y = ax² (a ≠ 0) và đồ thị của nó trong chương trình Toán 9. Đây là một chủ đề quan trọng, nền tảng cho các kiến thức toán học nâng cao hơn.
Bài học này sẽ cung cấp cho bạn một cái nhìn tổng quan về định nghĩa, các yếu tố cơ bản và cách vẽ đồ thị hàm số bậc hai một cách chính xác và hiệu quả.
1. Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) xác định với mọi giá trị x thuộc \(\mathbb{R}\).
1. Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)xác định với mọi giá trị x thuộc \(\mathbb{R}\). |
Ví dụ: Hàm số \(y = 2{x^2},y = - \frac{3}{2}{x^2}\) là các hàm số có dạng \(y = a{x^2}\left( {a \ne 0} \right)\).
2. Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
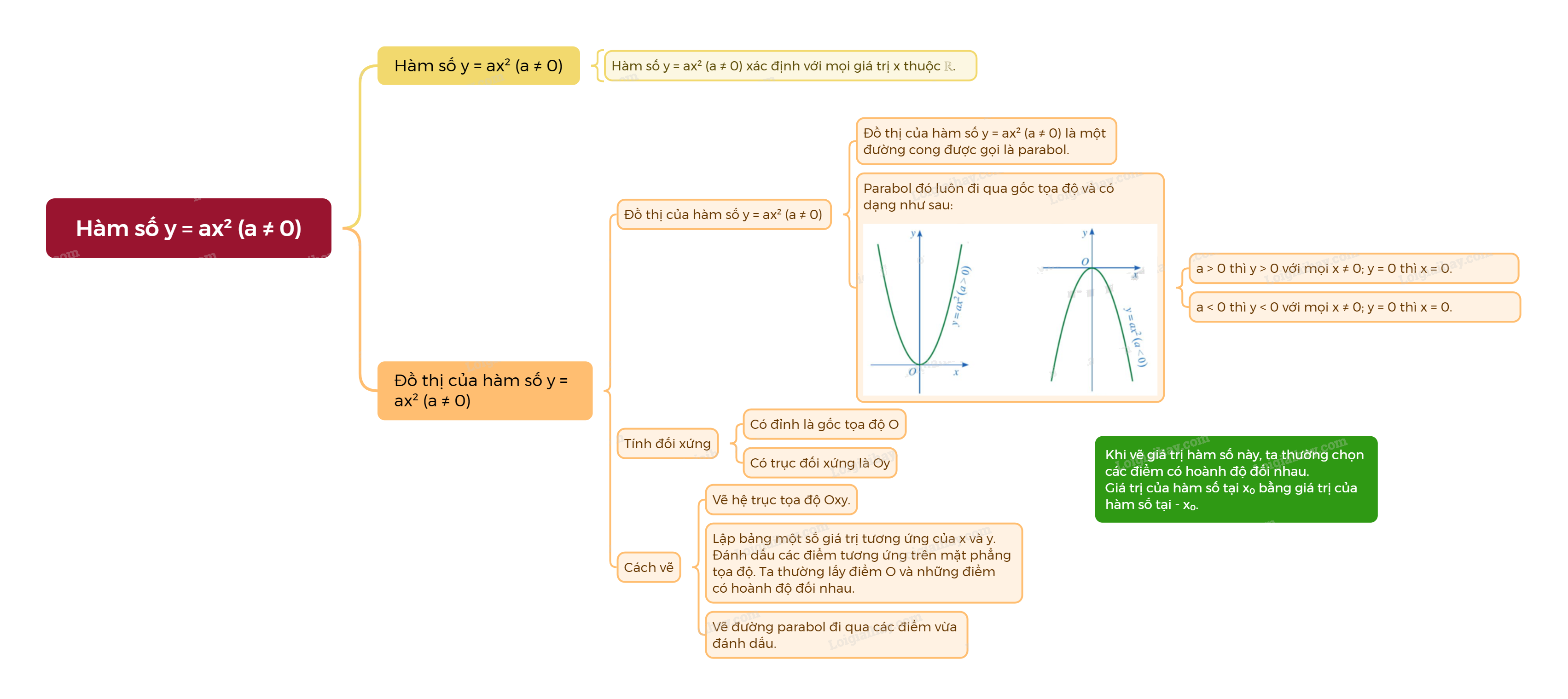
- Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) là một đường cong đi qua gốc tọa độ. Đường cong đó được gọi là một parabol với đỉnh O và nhận trục Oy làm trục đối xứng. - Nếu \(a > 0\) thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị. - Nếu \(a < 0\) thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị. |
Lưu ý:
- Cho hàm số \(y = a{x^2}\left( {a \ne 0} \right)\).
+ Nếu \(a > 0\) thì \(y > 0\) với mọi \(x \ne 0\); \(y = 0\) khi \(x = 0\).
+ Nếu \(a < 0\) thì \(y < 0\) với mọi \(x \ne 0\); \(y = 0\) khi \(x = 0\).
- Vì đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) luôn đi qua gốc tọa độ O và nhận trục Oy làm trục đối xứng nên khi vẽ giá trị của hàm số này, ta thường chọn những điểm có hoành độ đối nhau.
Chỉ cần tính giá trị của hàm số tại \({x_0}\), ta suy ra được giá trị của hàm số tại \( - {x_0}\) vì \(a{\left( { - x{ _0}} \right)^2} = a{x_0}^2\)
Cách vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
- Vẽ hệ trục tọa độ Oxy. - Lập bảng một số giá trị tương ứng của x và y. Đánh dấu các điểm tương ứng trên mặt phẳng tọa độ. Ta thường lấy điểm O và những điểm có hoành độ đối nhau. - Vẽ đường parabol đi qua các điểm vừa đánh dấu. |
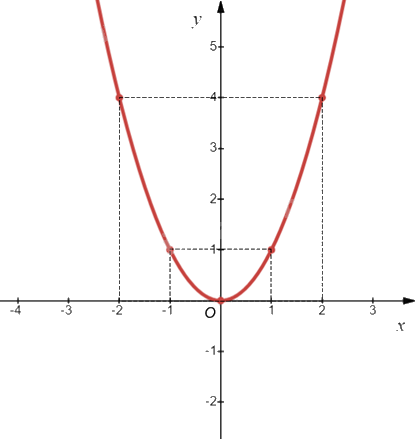
Ví dụ: Vẽ đồ thị của hàm số \(y = {x^2}\).
Bảng giá trị của hàm số:

Biểu diễn các điểm \(\left( { - 2;4} \right)\), \(\left( { - 1;1} \right)\), \(\left( {0;0} \right)\), \(\left( {1;1} \right)\), \(\left( {2;4} \right)\) trên mặt phẳng tọa độ Oxy và nối chúng lại với nhau, ta được đồ thị hàm số \(y = {x^2}\) như hình vẽ sau:
Hàm số bậc hai y = ax² (a ≠ 0) là một trong những hàm số quan trọng nhất trong chương trình Toán học THCS. Việc nắm vững lý thuyết và kỹ năng vẽ đồ thị hàm số này là điều kiện cần thiết để giải quyết các bài toán liên quan đến hàm số bậc hai, cũng như các bài toán ứng dụng trong thực tế.
Hàm số bậc hai có dạng tổng quát là y = ax² + bx + c, trong đó a, b, c là các số thực và a ≠ 0. Trong trường hợp đặc biệt, khi b = c = 0, hàm số trở thành y = ax² (a ≠ 0). Đây là hàm số bậc hai mà chúng ta sẽ tập trung nghiên cứu trong bài học này.
Hệ số a đóng vai trò quan trọng trong việc xác định hình dạng và hướng của parabol:
Ví dụ 1: Vẽ đồ thị hàm số y = 2x². Hệ số a = 2 > 0, parabol có hướng mở lên trên. Bảng giá trị:
| x | y |
|---|---|
| -2 | 8 |
| -1 | 2 |
| 0 | 0 |
| 1 | 2 |
| 2 | 8 |
Ví dụ 2: Vẽ đồ thị hàm số y = -x². Hệ số a = -1 < 0, parabol có hướng mở xuống dưới. Bảng giá trị:
| x | y |
|---|---|
| -2 | -4 |
| -1 | -1 |
| 0 | 0 |
| 1 | -1 |
| 2 | -4 |
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về lý thuyết hàm số y = ax² (a ≠ 0) và đồ thị của nó. Chúc bạn học tập tốt!