Chào mừng các em học sinh đến với bài giải bài tập 5.26 trang 121 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
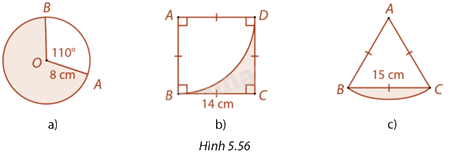
Tính chu vi và diện tích phần được tô màu trong mỗi trường hợp ở Hình 5.56. Làm tròn kết quả đến hàng phần mười.
Đề bài
Tính chu vi và diện tích phần được tô màu trong mỗi trường hợp ở Hình 5.56. Làm tròn kết quả đến hàng phần mười.
Phương pháp giải - Xem chi tiết
Công thức tính độ dài cung \({n^o}\) của đường tròn bán kính R: \(l = \frac{{\pi Rn}}{{180}}\).
Công thức tính diện tích hình quạt tròn bán kính R ứng với cung \({n^o}\): \({S_q} = \frac{{\pi {R^2}n}}{{360}}\).
Lời giải chi tiết
a) Góc AOB là góc ở tâm chắn cung nhỏ AB nên số đo cung AB nhỏ là bằng 110 độ.
Khi đó, số đo cung AB lớn bằng:
\({360^o} - {110^o} = {250^o}\).
Phần được tô màu là hình quạt tâm O, cung lớn AB nên
+ Diện tích phần tô màu là:
\(S = \frac{{\pi {{.8}^2}.250}}{{360}} = \frac{{400\pi }}{9} \approx 139,6\left( {c{m^2}} \right)\)
+ Độ dài cung AB lớn là:
\({l_{AB}} = \frac{{\pi .8.250}}{{180}} = \frac{{100\pi }}{9}\left( {cm} \right)\)
+ Chu vi hình được tô màu là:
\(C = OA + OB + {l_{AB}} = 8 + 8 + \frac{{100\pi }}{9} = 16 + \frac{{100\pi }}{9} \approx 50,9\left( {cm} \right)\)
b) Diện tích hình vuông ABCD là:
\({S_{ABCD}} = {14^2} = 196\left( {c{m^2}} \right)\)
Phần không tô màu là \(\frac{1}{4}\) hình tròn bán kính 14cm nên diện tích phần không tô màu là: \({S_1} = \frac{1}{4}{.5^2}.\pi = \frac{{25}}{4}\pi \left( {c{m^2}} \right)\).
Diện tích phần tô màu là:
\(S = {S_{ABCD}} - {S_1} = 196 - \frac{{25\pi }}{4} \approx 176,4\left( {c{m^2}} \right)\)
Độ dài cung BD là:
\({l_{BD}} = \frac{{\pi .14.90}}{{180}} = 7\pi \left( {cm} \right)\)
Chu vi phần được tô màu là:
\(C = DC + CB + {l_{BD}} = 14 + 14 + 7\pi = 28 + 7\pi \approx 50\left( {cm} \right)\)
c) Tam giác ABC có: \(AB = BC = CA\) nên tam giác ABC đều. Do đó, \(\widehat {BAC} = {60^o}\) nên hình quạt tâm A, hai bán kính AB, AC có số đo cung BC bằng 60 độ.
Diện tích hình quạt tâm A, cung BC là:
\({S_q} = \frac{{\pi {{.15}^2}.60}}{{360}} = \frac{{75\pi }}{2}\left( {c{m^2}} \right)\)
Diện tích tam giác đều ABC cạnh 15cm là:
\({S_{ABC}} = \frac{{{{15}^2}\sqrt 3 }}{4} = \frac{{225\sqrt 3 }}{4}\left( {c{m^2}} \right)\)
Do đó, diện tích phần được tô màu là:
\(S = {S_q} - {S_{ABC}} = \frac{{75\pi }}{2} - \frac{{225\sqrt 3 }}{4} \approx 20,4\left( {c{m^2}} \right)\)
Độ dài cung BC là:
\({l_{BC}} = \frac{{\pi .15.60}}{{180}} = 5\pi \left( {cm} \right)\).
Chu vi phần được tô màu là:
\({l_{BC}} + BC = 5\pi + 15 \approx 30,7\left( {cm} \right)\).
Bài tập 5.26 trang 121 SGK Toán 9 tập 1 yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết một bài toán thực tế liên quan đến việc xác định phương trình đường thẳng và ứng dụng của nó trong việc tìm điểm giao nhau của các đường thẳng.
Bài tập 5.26 thường có dạng như sau: Cho một hàm số y = ax + b và một điểm A(x0, y0). Hãy tìm giá trị của a và b sao cho đường thẳng y = ax + b đi qua điểm A và thỏa mãn một điều kiện nào đó (ví dụ: song song với một đường thẳng cho trước, vuông góc với một đường thẳng cho trước, cắt một đường thẳng khác tại một điểm cho trước).
Để giải bài tập 5.26, học sinh cần nắm vững các kiến thức sau:
Bài tập: Cho hàm số y = 2x + b. Tìm giá trị của b sao cho đường thẳng này đi qua điểm A(1, 3).
Giải:
Vì đường thẳng y = 2x + b đi qua điểm A(1, 3) nên ta có:
3 = 2 * 1 + b
=> b = 3 - 2 = 1
Vậy, giá trị của b là 1.
Để củng cố kiến thức và kỹ năng giải bài tập 5.26, học sinh nên luyện tập thêm các bài tập tương tự trong SGK Toán 9 tập 1 và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và tự tin hơn khi giải các bài tập khó.
Hy vọng với bài giải chi tiết và những hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải bài tập 5.26 trang 121 SGK Toán 9 tập 1. Chúc các em học tập tốt!