Chào mừng các em học sinh đến với bài giải bài tập 5.35 trang 127 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và áp dụng vào các bài tập tương tự.
Cho đường tròn (O; R). Từ điểm M nằm ngoài đường tròn với \(MO = 2R\), vẽ hai tiếp tuyến tiếp xúc (O) tại A và B. Viết công thức tính phần diện tích nằm ngoài đường tròn (O) của tứ giác MAOB theo R.
Đề bài
Cho đường tròn (O; R). Từ điểm M nằm ngoài đường tròn với \(MO = 2R\), vẽ hai tiếp tuyến tiếp xúc (O) tại A và B. Viết công thức tính phần diện tích nằm ngoài đường tròn (O) của tứ giác MAOB theo R.
Phương pháp giải - Xem chi tiết
+ Tính số đo góc AOM, từ đó tính được góc AOB, từ đó tính được số đo cung nhỏ AB.
+ Chứng minh \(\Delta OAM = \Delta OBM\left( {c.g.c} \right)\), suy ra \({S_{\Delta OAM}} = {S_{\Delta OBM}}\) nên \({S_{OAMB}} = {S_{\Delta OAM}} + {S_{\Delta OBM}} = 2{S_{\Delta OAM}}\).
+ Diện tích hình quạt tâm O, cung nhỏ AB là: ${{S}_{q}}=\frac{\pi .O{{A}^{2}}.sđ{{\overset\frown{AB}}_{nhỏ}}}{{{360}^{o}}}$.
+ Diện tích nằm ngoài đường tròn (O) của tứ giác MAOB là: \(S = {S_{OAMB}} - {S_q}\).
Lời giải chi tiết
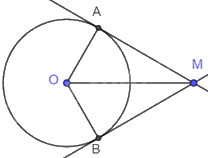
Vì MA, MB là tiếp tuyến của (O) nên
+ \(MA = MB\).
+ OA là tia phân giác của góc AOB, suy ra \(\widehat {AOM} = \widehat {MOB} = \frac{1}{2}\widehat {AOB}\).
Vì MA là tiếp tuyến của (O) nên \(MA \bot AO\) nên \(\Delta AOM\) vuông tại A. Suy ra:
+ \(AM = \sqrt {M{O^2} - A{O^2}} = \sqrt {{{\left( {2R} \right)}^2} - {R^2}} = \sqrt 3 R\).
+ \(\cos AOM = \frac{{OA}}{{OM}} = \frac{R}{{2R}} = \frac{1}{2}\) nên \(\widehat {AOM} = {60^o}\), suy ra \(\widehat {AOB} = {2.60^o} = {120^o}\).
Vì AOB là góc ở tâm chắn cung nhỏ AB nên số đo cung nhỏ AB bằng 120 độ.
Vì tam giác AOM vuông tại A nên
\({S_{AOM}} = \frac{1}{2}OA.AM = \frac{1}{2}.R.R\sqrt 3 = \frac{{{R^2}\sqrt 3 }}{3}\).
Tam giác OAM và tam giác OBM có:
\(OA = OB\) (= bán kính (O)),
\(OM\) chung,
\(\widehat {AOM} = \widehat {MOB}\left( {cmt} \right)\)
Do đó, \(\Delta OAM = \Delta OBM\left( {c.g.c} \right)\).
Suy ra, \({S_{OAMB}} = {S_{\Delta OAM}} + {S_{\Delta OBM}} = 2{S_{\Delta OAM}} = \frac{{2{R^2}\sqrt 3 }}{3}\).
Diện tích hình quạt tâm O, cung nhỏ AB là:
${{S}_{q}}=\frac{\pi .O{{A}^{2}}.sđ{{\overset\frown{AB}}_{nhỏ}}}{360}=\frac{\pi .{{R}^{2}}.120}{360}=\frac{\pi .{{R}^{2}}}{3}$.
Diện tích nằm ngoài đường tròn (O) của tứ giác MAOB là: \(S = {S_{OAMB}} - {S_q} = \frac{{2{R^2}\sqrt 3 }}{3} - \frac{{\pi .{R^2}}}{3} = \frac{{{R^2}}}{3}\left( {2\sqrt 3 - \pi } \right)\).
Bài tập 5.35 trang 127 SGK Toán 9 tập 1 yêu cầu chúng ta giải một bài toán liên quan đến hàm số bậc nhất và ứng dụng thực tế. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về hàm số bậc nhất, cách xác định hệ số góc và tung độ gốc, cũng như cách vẽ đồ thị hàm số.
Hàm số bậc nhất có dạng y = ax + b, trong đó a là hệ số góc và b là tung độ gốc.
Trước khi đi vào giải bài tập cụ thể, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Thông thường, bài toán sẽ cho một tình huống thực tế và yêu cầu chúng ta xây dựng hàm số bậc nhất mô tả mối quan hệ giữa các đại lượng trong tình huống đó.
(Nội dung lời giải chi tiết bài tập 5.35 sẽ được trình bày tại đây. Bao gồm các bước giải, giải thích rõ ràng từng bước và kết luận cuối cùng. Ví dụ:)
Giả sử bài toán yêu cầu tìm hàm số biểu diễn chi phí vận chuyển hàng hóa theo quãng đường vận chuyển. Chúng ta có thể đặt x là quãng đường vận chuyển (km) và y là chi phí vận chuyển (đồng). Dựa vào thông tin đề bài cung cấp, chúng ta có thể xác định được hai điểm thuộc đồ thị hàm số. Sau đó, chúng ta sử dụng công thức tính hệ số góc và tung độ gốc để xác định hàm số y = ax + b.
Để giúp các em hiểu rõ hơn về cách giải bài tập hàm số bậc nhất, chúng ta sẽ xem xét một số ví dụ minh họa và bài tập tương tự.
Hàm số bậc nhất có rất nhiều ứng dụng trong thực tế, chẳng hạn như:
Để nắm vững kiến thức về hàm số bậc nhất và ứng dụng, các em nên luyện tập thêm nhiều bài tập khác nhau. Các em có thể tìm thấy các bài tập này trong SGK Toán 9 tập 1, sách bài tập Toán 9, hoặc trên các trang web học toán online như giaitoan.edu.vn.
Bài tập 5.35 trang 127 SGK Toán 9 tập 1 là một bài tập điển hình về ứng dụng của hàm số bậc nhất. Bằng cách nắm vững lý thuyết và luyện tập thường xuyên, các em sẽ có thể giải quyết bài tập này một cách dễ dàng và hiệu quả.
Hy vọng rằng bài giải chi tiết này sẽ giúp các em hiểu rõ hơn về bài tập 5.35 trang 127 SGK Toán 9 tập 1. Chúc các em học tập tốt!