Chào mừng các em học sinh đến với bài giải bài tập 4.1 trang 82 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương Hàm số bậc nhất và là một phần quan trọng trong việc củng cố kiến thức về hàm số.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin làm bài tập.
Tính tỉ số lượng giác của các góc \(\alpha \) và \(\beta \) trong mỗi trường hợp ở Hình 4.13.
Đề bài
Tính tỉ số lượng giác của các góc \(\alpha \) và \(\beta \) trong mỗi trường hợp ở Hình 4.13.
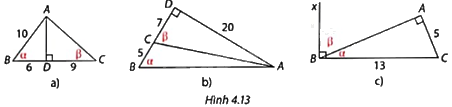
Phương pháp giải - Xem chi tiết
a, b, c) Sử dụng kiến thức về tỉ số lượng giác của góc nhọn để tính: Trong tam giác vuông có góc nhọn \(\alpha \), khi đó:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là \(\sin \alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là \(\cos \alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là \(\tan \alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là \(\cot \alpha \).
c) Sử dụng kiến thức để tính góc \(\beta \): Nếu hai góc phụ nhau thì sin của góc này bằng côsin của góc kia, tang của góc này bằng côtang của góc kia.
Lời giải chi tiết
Hình a: \(\Delta \)ADB vuông tại D nên \(A{D^2} + D{B^2} = A{B^2}\) (Định lí Pythagore).
Suy ra: \(A{D^2} = A{B^2} - B{D^2} = {10^2} - {6^2} = 64\).
Do đó, \(AD = 8\).
Suy ra, \(\sin \alpha = \frac{{AD}}{{AB}} = \frac{8}{{10}} = \frac{4}{5}\), \(\cos \alpha = \frac{{BD}}{{AB}} = \frac{6}{{10}} = \frac{3}{5}\), \(\tan \alpha = \frac{{AD}}{{BD}} = \frac{8}{6} = \frac{4}{3}\), \(\cot \alpha = \frac{{BD}}{{AD}} = \frac{6}{8} = \frac{3}{4}\).
\(\Delta \)ADC vuông tại D nên \(A{C^2} = A{D^2} + D{C^2} = {9^2} + 64 = 145\) (Định lí Pythagore). Do đó, \(AC = \sqrt {145} \)
Do đó, \(\sin \beta = \frac{{AD}}{{AC}} = \frac{8}{{\sqrt {145} }}\), \(\cos \beta = \frac{{DC}}{{AC}} = \frac{9}{{\sqrt {145} }}\), \(\tan \beta = \frac{{AD}}{{DC}} = \frac{8}{9}\), \(\cot \beta = \frac{{DC}}{{AD}} = \frac{9}{8}\).
Hình b:
\(\Delta \)ADC vuông tại D nên \(A{C^2} = A{D^2} + D{C^2} = {7^2} + {20^2} = 449\) (Định lí Pythagore). Do đó, \(AC = \sqrt {449} \).
Do đó, \(\sin \beta = \frac{{AD}}{{AC}} = \frac{{20}}{{\sqrt {449} }}\), \(\cos \beta = \frac{{DC}}{{AC}} = \frac{7}{{\sqrt {449} }}\), \(\tan \beta = \frac{{AD}}{{DC}} = \frac{{20}}{7}\), \(\cot \beta = \frac{{DC}}{{AD}} = \frac{7}{{20}}\).
\(\Delta \)ADB vuông tại D nên \(A{B^2} = A{D^2} + D{B^2} = {12^2} + {20^2} = 544\) (Định lí Pythagore). Do đó, \(AB = 4\sqrt {34} \).
Do đó, \(\sin \alpha = \frac{{AD}}{{AB}} = \frac{{20}}{{4\sqrt {34} }} = \frac{{5\sqrt {34} }}{{34}}\), \(\cos \alpha = \frac{{DB}}{{AB}} = \frac{{12}}{{4\sqrt {34} }} = \frac{{3\sqrt {34} }}{{34}}\), \(\tan \alpha = \frac{{AD}}{{DB}} = \frac{{20}}{{12}} = \frac{5}{3}\), \(\cot \alpha = \frac{{DB}}{{AD}} = \frac{{12}}{{20}} = \frac{3}{5}\).
Hình c: \(\Delta \)ABC vuông tại A nên \(B{C^2} = A{B^2} + A{C^2}\) (Định lí Pythagore).
Do đó, \(AB = \sqrt {B{C^2} - A{C^2}} = \sqrt {{{13}^2} - {5^2}} = 12\).
Suy ra, \(\sin \alpha = \frac{{AC}}{{BC}} = \frac{5}{{13}}\), \(\cos \alpha = \frac{{AB}}{{BC}} = \frac{{12}}{{13}}\), \(\tan \alpha = \frac{{AC}}{{AB}} = \frac{5}{{12}}\), \(\cot \alpha = \frac{{AB}}{{AC}} = \frac{{12}}{5}\).
Vì \(\alpha + \beta = {90^o}\) nên \(\sin \beta = \cos \alpha = \frac{{12}}{{13}}\), \(\cos \beta = \sin \alpha = \frac{5}{{13}}\), \(\tan \beta = \cot \alpha = \frac{{12}}{5}\), \(\cot \beta = \tan \alpha = \frac{5}{{12}}\)
Bài tập 4.1 trang 82 SGK Toán 9 tập 1 yêu cầu chúng ta xác định hàm số bậc nhất và các hệ số a, b của hàm số đó. Để giải bài tập này, chúng ta cần nắm vững định nghĩa về hàm số bậc nhất và cách xác định các hệ số.
Hàm số bậc nhất là hàm số có dạng y = ax + b, trong đó a và b là các số thực, a ≠ 0.
Để giải bài tập 4.1, chúng ta cần xem xét từng hàm số được đưa ra và xác định xem nó có dạng y = ax + b hay không. Nếu có, chúng ta sẽ xác định giá trị của a và b.
Ví dụ, xét hàm số y = 2x + 3. Hàm số này có dạng y = ax + b, với a = 2 và b = 3. Do đó, đây là một hàm số bậc nhất với hệ số góc là 2 và tung độ gốc là 3.
Ngoài việc xác định hàm số bậc nhất, bài tập về hàm số bậc nhất còn có thể yêu cầu chúng ta:
Để giải bài tập về hàm số bậc nhất một cách hiệu quả, chúng ta nên:
Để củng cố kiến thức, các em có thể làm thêm các bài tập tương tự sau:
Hàm số bậc nhất có rất nhiều ứng dụng trong thực tế, ví dụ như:
Bài tập 4.1 trang 82 SGK Toán 9 tập 1 là một bài tập cơ bản nhưng quan trọng trong chương Hàm số bậc nhất. Việc nắm vững kiến thức và kỹ năng giải bài tập này sẽ giúp các em học tốt môn Toán và ứng dụng vào thực tế.
Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em sẽ tự tin giải bài tập 4.1 trang 82 SGK Toán 9 tập 1 và các bài tập tương tự. Chúc các em học tốt!
| Hàm số | Hệ số a | Hệ số b |
|---|---|---|
| y = 2x + 3 | 2 | 3 |
| y = -x + 1 | -1 | 1 |