Phương trình quy về bậc nhất một ẩn là một trong những chủ đề quan trọng trong chương trình Toán 9. Việc nắm vững lý thuyết và kỹ năng giải loại phương trình này là nền tảng để học tốt các kiến thức toán học nâng cao hơn.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu cùng với các bài tập minh họa giúp bạn hiểu rõ bản chất của phương trình và cách giải chúng một cách hiệu quả.
1. Phương trình tích có dạng (left( {ax + b} right)left( {cx + d} right) = 0left( {a ne 0,c ne 0} right)) Cách giải phương trình tích
1. Phương trình tích có dạng \(\left( {ax + b} \right)\left( {cx + d} \right) = 0\left( {a \ne 0,c \ne 0} \right)\)
Cách giải phương trình tích
Để giải phương trình tích \(\left( {ax + b} \right)\left( {cx + d} \right) = 0\) với \(a \ne 0\) và \(c \ne 0\), ta có thể làm như sau: Bước 1.Giải hai phương trình \(ax + b = 0\) và \(cx + d = 0\) Bước 2.Nghiệm của mỗi phương trình ở Bước 1 là nghiệm của phương trình \(\left( {ax + b} \right)\left( {cx + d} \right) = 0\). |
Ví dụ 1:Giải phương trình \(\left( {2x + 1} \right)\left( {3x - 1} \right) = 0\)
Lời giải:
Để giải phương trình \(\left( {2x + 1} \right)\left( {3x - 1} \right) = 0\), ta giải hai phương trình sau:
*) \(2x + 1 = 0\)
\(2x = - 1\)
\(x = - \frac{1}{2}\).
*) \(3x - 1 = 0\)
\(3x = 1\)
\(x = \frac{1}{3}\).
Vậy phương trình đã cho có hai nghiệm là \(x = - \frac{1}{2}\) và \(x = \frac{1}{3}\).
Ví dụ 2: Giải phương trình \({x^2} - x = - 2x + 2\).
Lời giải:
Biến đổi phương trình đã cho về phương trình tích như sau:
\(\begin{array}{l}{x^2} - x = - 2x + 2\\{x^2} - x + 2x - 2 = 0\\x\left( {x - 1} \right) + 2\left( {x - 1} \right) = 0\\\left( {x + 2} \right)\left( {x - 1} \right) = 0.\end{array}\)
Ta giải hai phương trình sau:
*) \(x + 2 = 0\)
\(x = - 2\).
*) \(x - 1 = 0\)
\(x = 1\).
Vậy phương trình đã cho có hai nghiệm là \(x = - 2\) và \(x = 1\).
2. Phương trình chứa ẩn ở mẫu
Điều kiện xác định của phương trình chứa ẩn ở mẫu
Điều kiện xác định của phương trình chứa ẩn ở mẫu là điều kiện của ẩn để tất cả các mẫu trong phương trình đều khác 0. |
Ví dụ:
- Phương trình \(\frac{{5x + 2}}{{x - 1}} = 0\) có điều kiện xác định là \(x - 1 \ne 0\) hay \(x \ne 1\).
- Phương trình \(\frac{1}{{x + 1}} = 1 + \frac{1}{{x - 2}}\) có điều kiện xác định là \(x + 1 \ne 0\) và \(x - 2 \ne 0\) hay \(x \ne - 1\) và \(x \ne 2\).
Các bước giải phương trình chứa ẩn ở mẫu
Bước 1.Tìm điều kiện xác định của phương trình. Bước 2. Quy đồng mẫu hai vế của phương trình rồi bỏ mẫu. Bước 3.Giải phương trình vừa nhận được. Bước 4. Kiểm tra điều kiện xác định và kết luận nghiệm của phương trình ban đầu. |
Ví dụ: Giải phương trình \(\frac{2}{{x + 1}} + \frac{1}{{x - 2}} = \frac{3}{{\left( {x + 1} \right)\left( {x - 2} \right)}}\)
Lời giải:
Điều kiện xác định \(x \ne - 1\) và \(x \ne 2\).
\(\frac{2}{{x + 1}} + \frac{1}{{x - 2}} = \frac{3}{{\left( {x + 1} \right)\left( {x - 2} \right)}}\)
\(\frac{{2\left( {x - 2} \right) + \left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {x - 2} \right)}} = \frac{3}{{\left( {x + 1} \right)\left( {x - 2} \right)}}\)
\(2\left( {x - 2} \right) + \left( {x + 1} \right) = 3\).
\(\begin{array}{l}2\left( {x - 2} \right) + \left( {x + 1} \right) = 3\\2x - 4 + x + 1 = 3\\3x - 3 = 3\\3x = 6\\x = 2\end{array}\)
Ta thấy \(x = 2\) không thỏa mãn điều kiện xác định của phương trình.
Vậy phương trình \(\frac{2}{{x + 1}} + \frac{1}{{x - 2}} = \frac{3}{{\left( {x + 1} \right)\left( {x - 2} \right)}}\) vô nghiệm.
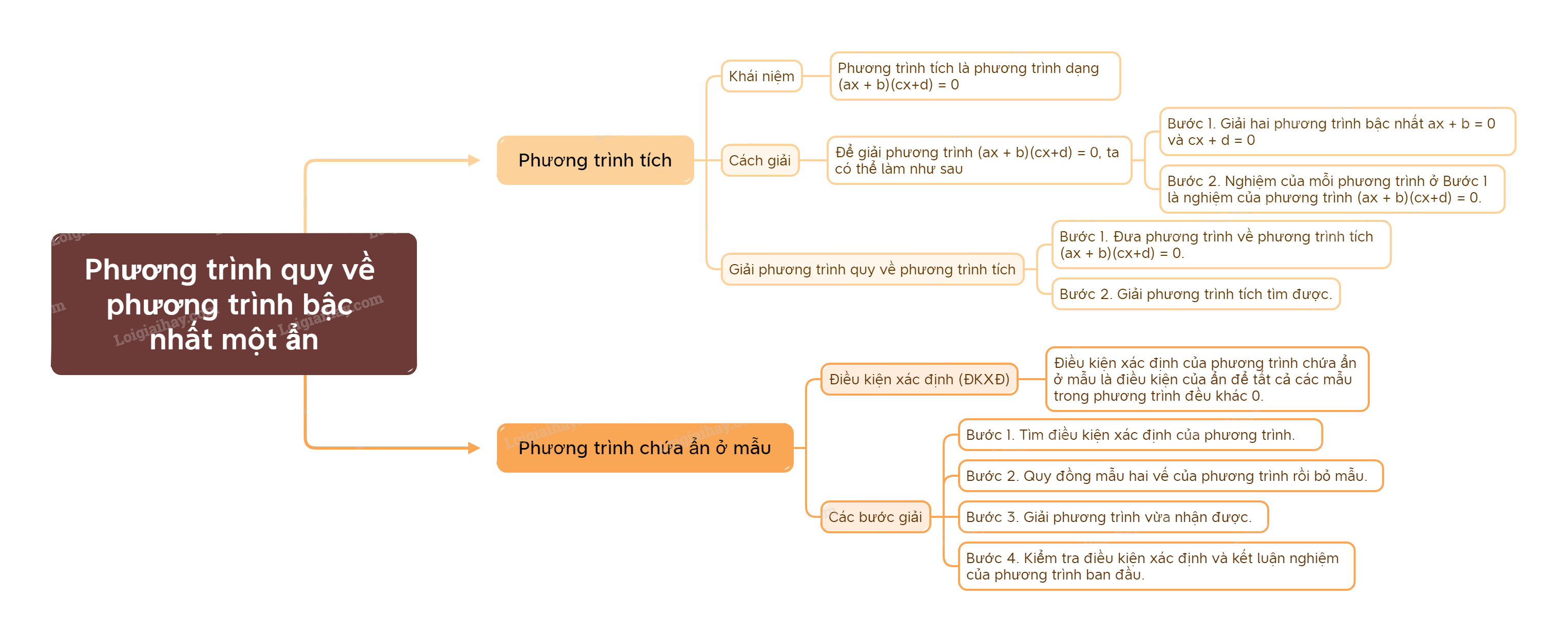
Trong chương trình Toán 9, phương trình quy về bậc nhất một ẩn đóng vai trò quan trọng trong việc rèn luyện tư duy logic và kỹ năng giải toán. Hiểu rõ lý thuyết và phương pháp giải các loại phương trình này là bước đệm vững chắc cho việc học tập các kiến thức toán học phức tạp hơn ở các lớp trên.
Phương trình quy về bậc nhất một ẩn là phương trình mà sau khi thực hiện các phép biến đổi đại số (như khử mẫu, bỏ ngoặc, chuyển vế, rút gọn), ta được một phương trình có dạng:
ax + b = 0
Trong đó:
Có nhiều dạng phương trình khác nhau có thể quy về dạng bậc nhất một ẩn. Dưới đây là một số dạng phổ biến:
Để giải phương trình chứa mẫu số, ta cần thực hiện các bước sau:
Ví dụ: Giải phương trình 1/x + 2 = 3
Giải:
Vậy nghiệm của phương trình là x = 1.
Để giải phương trình chứa ngoặc, ta cần thực hiện các bước sau:
Ví dụ: Giải phương trình 2(x - 1) + 3 = 5
Giải:
Vậy nghiệm của phương trình là x = 2.
Tương tự như phương trình chứa mẫu số, ta cần tìm điều kiện xác định trước khi giải.
Các bước giải phương trình quy về bậc nhất một ẩn thường bao gồm:
Dưới đây là một số bài tập để bạn luyện tập:
Khi giải phương trình quy về bậc nhất một ẩn, cần lưu ý:
Hy vọng với những kiến thức và hướng dẫn trên, bạn sẽ nắm vững lý thuyết và kỹ năng giải phương trình quy về bậc nhất một ẩn Toán 9. Chúc bạn học tập tốt!