Chào mừng bạn đến với bài học về Lý thuyết Đa giác đều trong chương trình Toán 9 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp cho bạn một cách đầy đủ và dễ hiểu nhất về khái niệm, tính chất và các ứng dụng của đa giác đều.
Chúng ta sẽ cùng nhau khám phá những kiến thức quan trọng, giúp bạn tự tin giải quyết các bài tập liên quan đến chủ đề này.
1. Đa giác Đa giác ABCDE: + Các đỉnh là các điểm: A, B, C, D, E; + Các cạnh là các đoạn thẳng: AB, BC, CD, DE, AE; + Các cặp đỉnh kề nhau là: A và B, B và C, C và D, D và E, E và A;
1. Đa giác
Đa giác ABCDE:
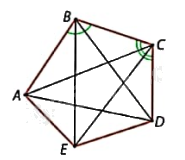
+ Các đỉnh là các điểm: A, B, C, D, E;
+ Các cạnh là các đoạn thẳng: AB, BC, CD, DE, AE;
+ Các cặp đỉnh kề nhau là: A và B, B và C, C và D, D và E, E và A;
+ Các đường chéo là các đoạn thẳng nối hai đỉnh không kề nhau: AC, AD, BD, BE, CE;
+ Các góc \(\widehat {ABC},\widehat {BCD},\widehat {CDE},\widehat {DEA},\widehat {EAB}\).
- Đa giác có n đỉnh (\(n \ge 3\)) được gọi là hình n – giác hay hình n cạnh,
Ta thường gọi các đa giác có 3, 4, 5, 6, 8 đỉnh là tam giác, tứ giác, ngũ giác, lục giác, bát giác.
2. Đa giác đều
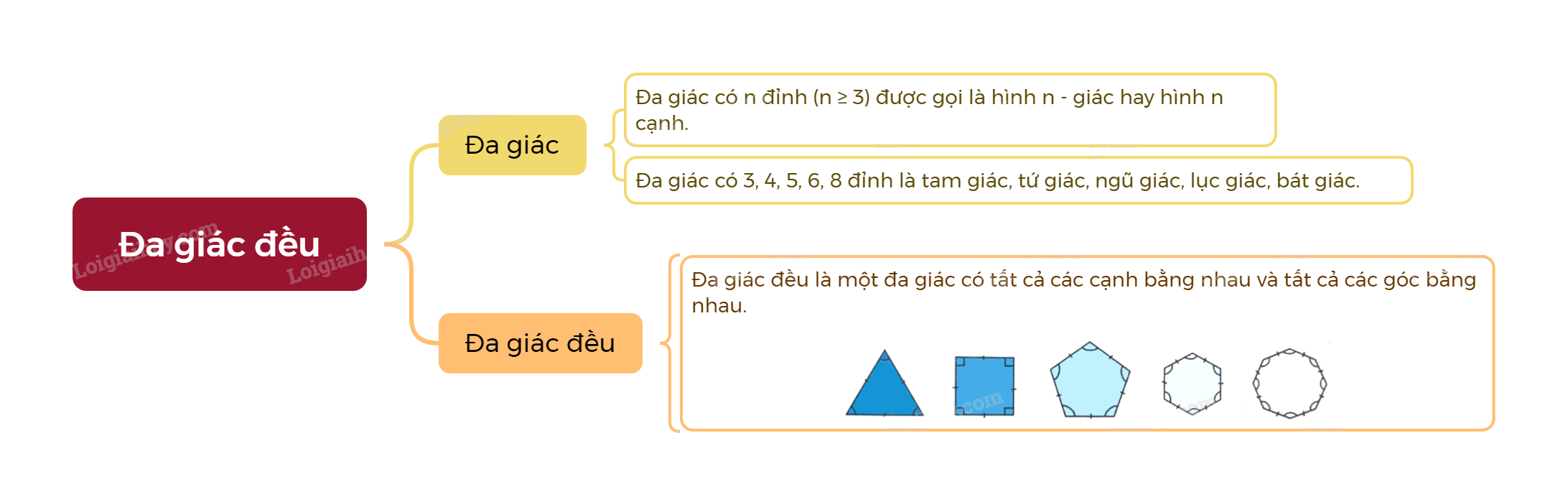
Đa giác đều là một đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau. |
Ví dụ: Một số hình đa giác đều thường gặp trong hình học:

3. Một số hình phẳng đều trong thực tiễn
Ví dụ: Một số hình phẳng đều trong thực tế:

Đa giác đều là một đa giác lồi có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau. Để hiểu rõ hơn về đa giác đều, chúng ta cần nắm vững các khái niệm sau:
Đa giác đều có những tính chất đặc biệt sau:
Dưới đây là một số công thức quan trọng cần nhớ:
Một số loại đa giác đều phổ biến:
Hãy thử giải các bài tập sau để củng cố kiến thức:
Đa giác đều xuất hiện rất nhiều trong cuộc sống hàng ngày, ví dụ:
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về Lý thuyết Đa giác đều Toán 9. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải quyết các bài tập liên quan. Chúc bạn học tốt tại giaitoan.edu.vn!