Chào mừng các em học sinh đến với bài giải bài tập 5.44 trang 129 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương Hàm số bậc nhất và ứng dụng. Chúng tôi sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
Giaitoan.edu.vn là nền tảng học toán online uy tín, cung cấp đầy đủ các bài giải SGK Toán 9, bài tập trắc nghiệm, và các tài liệu học tập hữu ích khác.
Cho MA và MB là hai tiếp tuyến của đường tròn (O; R) (A, B là hai tiếp điểm) sao cho \(\Delta \)MAB là tam giác đều. Khoảng cách OM bằng A. \(\frac{1}{2}R\). B. R. C. 2R. D. \(R\sqrt 2 \).
Đề bài
Cho MA và MB là hai tiếp tuyến của đường tròn (O; R) (A, B là hai tiếp điểm) sao cho \(\Delta \)MAB là tam giác đều. Khoảng cách OM bằng
A. \(\frac{1}{2}R\).
B. R.
C. 2R.
D. \(R\sqrt 2 \).
Phương pháp giải - Xem chi tiết
+ Chứng minh \(\widehat {AMB} = {60^o}\).
+ Chứng minh MO là tia phân giác \(\widehat {AMB}\), nên \(\widehat {AMO} = \frac{1}{2}\widehat {AMB}\).
+ Chứng minh tam giác AOM vuông tại M nên \(AO = MO.\sin AMO\), từ đó tính được MO.
Lời giải chi tiết
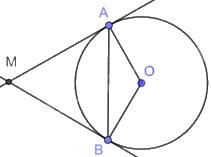
Vì tam giác MAB đều nên \(\widehat {AMB} = {60^o}\).
Vì MA và MB là tiếp tuyến của (O) nên MO là tia phân giác \(\widehat {AMB}\), nên \(\widehat {AMO} = \frac{1}{2}\widehat {AMB} = \frac{1}{2}{.60^o} = {30^o}\)
Vì MA là tiếp tuyến của (O) nên \(MA \bot AO\). Do đó, tam giác MAO vuông tại A.
Suy ra, \(AO = MO.\sin AMO\) nên
\(MO = \frac{{AO}}{{\sin AMO}} = \frac{R}{{\sin {{30}^o}}} = 2R\).
Chọn C
Bài tập 5.44 trang 129 SGK Toán 9 tập 1 yêu cầu chúng ta vận dụng kiến thức về phương pháp tiếp tuyến để giải quyết một bài toán thực tế. Cụ thể, bài toán thường liên quan đến việc xác định phương trình tiếp tuyến của một đường thẳng hoặc đường cong tại một điểm cho trước.
Trước khi đi vào giải chi tiết, chúng ta cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Thông thường, bài toán sẽ cung cấp thông tin về một đường thẳng hoặc đường cong, một điểm, và yêu cầu tìm phương trình tiếp tuyến tại điểm đó.
(Nội dung lời giải chi tiết sẽ được trình bày tại đây, bao gồm các bước giải cụ thể, các phép tính, và giải thích rõ ràng. Ví dụ:)
Ví dụ: Giả sử bài toán yêu cầu tìm phương trình tiếp tuyến của đường thẳng y = x2 tại điểm có hoành độ x = 2.
Ngoài bài tập 5.44, còn rất nhiều bài tập tương tự liên quan đến phương pháp tiếp tuyến. Các bài tập này có thể khác nhau về dạng đường cong (parabol, elip, hypebol…) và các thông tin đã cho. Tuy nhiên, phương pháp giải cơ bản vẫn là:
Để củng cố kiến thức và kỹ năng giải bài tập về phương pháp tiếp tuyến, các em có thể tự giải thêm các bài tập sau:
Bài tập 5.44 trang 129 SGK Toán 9 tập 1 là một bài tập quan trọng giúp các em hiểu rõ hơn về phương pháp tiếp tuyến và ứng dụng của nó trong giải toán. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em sẽ tự tin giải quyết bài tập này và các bài tập tương tự một cách hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!