Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 2 trang 117, 118, 119 SGK Toán 9 tập 1. Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán và tự tin giải quyết các bài tập tương tự.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết cung cấp những lời giải chính xác, dễ hiểu và phù hợp với trình độ của học sinh.
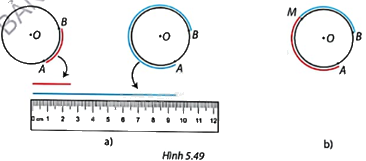
Cắt một hình tròn bằng giấy và đánh dấu hai điểm A, B bất kì trên mép của hình tròn. a) Sử dụng dây mềm để lần lượt viền theo hai cung AB như Hình 5.49a và đo độ dài của đoạn dây trong mỗi trường hợp. b) Lấy một điểm M bất kì trên cung AB, chia cung AB thành hai cung AM và MB. So sánh tổng độ dài hai đoạn dây được viền theo cung AB và MB với độ dài đoạn dây được viền theo cung AB (Hình 5.49b).
Trả lời câu hỏi Luyện tập 2 trang 119 SGK Toán 9 Cùng khám phá
Tính độ dài cung \({235^o}\) của đường tròn bán kính 7cm.
Phương pháp giải:
Công thức tính độ dài cung \({n^o}\) của đường tròn bán kính R: \(l = \frac{{\pi Rn}}{{180}}\).
Lời giải chi tiết:
Độ dài cung \({235^o}\) của đường tròn bán kính 7cm là:
\(l = \frac{{\pi .7.235}}{{180}} = \frac{{329\pi }}{{36}}\left( {cm} \right)\).
Trả lời câu hỏi Hoạt động 2 trang 117 SGK Toán 9 Cùng khám phá
Cắt một hình tròn bằng giấy và đánh dấu hai điểm A, B bất kì trên mép của hình tròn.
a) Sử dụng dây mềm để lần lượt viền theo hai cung AB như Hình 5.49a và đo độ dài của đoạn dây trong mỗi trường hợp.
b) Lấy một điểm M bất kì trên cung AB, chia cung AB thành hai cung AM và MB. So sánh tổng độ dài hai đoạn dây được viền theo cung AB và MB với độ dài đoạn dây được viền theo cung AB (Hình 5.49b).
Phương pháp giải:
a) Ta đo được độ dài đoạn dây AB trong hai trường hợp lần lượt là 2,5cm và 7,5cm.
b) Thực hiện đo và ta đưa ra được kết luận: \(MA + MB = AB\).
Lời giải chi tiết:
a) Ta đo được độ dài doạn dây AB trong hai trường hợp lần lượt là 2,5cm và 7,5cm.
b) Thực hiện đo và ta đưa ra được kết luận: \(MA + MB = AB\).
Trả lời câu hỏi Hoạt động 3 trang 118 SGK Toán 9 Cùng khám phá
Quay lại hoạt động gấp hình tròn trong Hoạt động 1.
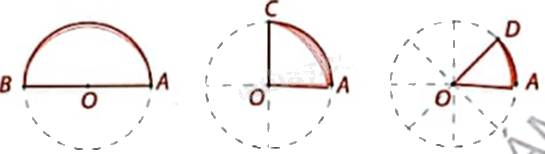
Hãy xác định các số đo cung và tỉ số trong các ô ? của bảng dưới đây. Em có nhận xét gì?

Phương pháp giải:
+ Số đo các cung AB, AC, AD lần lượt có số đo là \({180^o}\), \({90^o}\), \({45^o}\).
+ Tỉ số của số đo cung và \({360^o}\) bằng thương giữa số đo cung tương ứng và \({360^o}\).
+ Tỉ số của độ dài cung và độ dài đường tròn bằng thương giữa độ dài cung tương ứng và độ dài đường tròn.
+ Nhận xét: Độ dài cung tỉ lệ thuận với số đo của nó.
Lời giải chi tiết:

Nhận xét: Độ dài cung tỉ lệ thuận với số đo của nó.
Trả lời câu hỏi Hoạt động 2 trang 117 SGK Toán 9 Cùng khám phá
Cắt một hình tròn bằng giấy và đánh dấu hai điểm A, B bất kì trên mép của hình tròn.
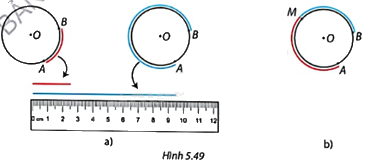
a) Sử dụng dây mềm để lần lượt viền theo hai cung AB như Hình 5.49a và đo độ dài của đoạn dây trong mỗi trường hợp.
b) Lấy một điểm M bất kì trên cung AB, chia cung AB thành hai cung AM và MB. So sánh tổng độ dài hai đoạn dây được viền theo cung AB và MB với độ dài đoạn dây được viền theo cung AB (Hình 5.49b).
Phương pháp giải:
a) Ta đo được độ dài đoạn dây AB trong hai trường hợp lần lượt là 2,5cm và 7,5cm.
b) Thực hiện đo và ta đưa ra được kết luận: \(MA + MB = AB\).
Lời giải chi tiết:
a) Ta đo được độ dài doạn dây AB trong hai trường hợp lần lượt là 2,5cm và 7,5cm.
b) Thực hiện đo và ta đưa ra được kết luận: \(MA + MB = AB\).
Trả lời câu hỏi Hoạt động 3 trang 118 SGK Toán 9 Cùng khám phá
Quay lại hoạt động gấp hình tròn trong Hoạt động 1.
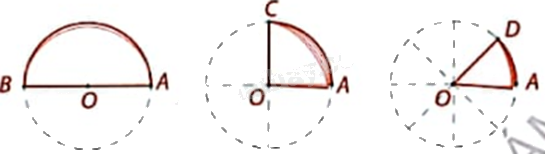
Hãy xác định các số đo cung và tỉ số trong các ô ? của bảng dưới đây. Em có nhận xét gì?

Phương pháp giải:
+ Số đo các cung AB, AC, AD lần lượt có số đo là \({180^o}\), \({90^o}\), \({45^o}\).
+ Tỉ số của số đo cung và \({360^o}\) bằng thương giữa số đo cung tương ứng và \({360^o}\).
+ Tỉ số của độ dài cung và độ dài đường tròn bằng thương giữa độ dài cung tương ứng và độ dài đường tròn.
+ Nhận xét: Độ dài cung tỉ lệ thuận với số đo của nó.
Lời giải chi tiết:

Nhận xét: Độ dài cung tỉ lệ thuận với số đo của nó.
Trả lời câu hỏi Luyện tập 2 trang 119 SGK Toán 9 Cùng khám phá
Tính độ dài cung \({235^o}\) của đường tròn bán kính 7cm.
Phương pháp giải:
Công thức tính độ dài cung \({n^o}\) của đường tròn bán kính R: \(l = \frac{{\pi Rn}}{{180}}\).
Lời giải chi tiết:
Độ dài cung \({235^o}\) của đường tròn bán kính 7cm là:
\(l = \frac{{\pi .7.235}}{{180}} = \frac{{329\pi }}{{36}}\left( {cm} \right)\).
Mục 2 của SGK Toán 9 tập 1 thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững kiến thức lý thuyết, các định nghĩa, định lý và công thức liên quan. Việc hiểu rõ bản chất của vấn đề là yếu tố then chốt để tìm ra phương pháp giải phù hợp.
Bài tập này thường yêu cầu học sinh vận dụng kiến thức về... (giả sử bài tập liên quan đến hàm số bậc nhất). Để giải bài tập này, ta cần xác định được các yếu tố quan trọng như hệ số góc, giao điểm với trục tọa độ và các điểm đặc biệt của hàm số. Sau đó, áp dụng các công thức và phương pháp đã học để tìm ra kết quả chính xác.
Bài tập này có thể liên quan đến việc... (giả sử bài tập liên quan đến hệ phương trình bậc nhất hai ẩn). Để giải bài tập này, ta có thể sử dụng phương pháp thế hoặc phương pháp cộng đại số. Việc lựa chọn phương pháp phù hợp sẽ giúp ta giải quyết bài toán một cách nhanh chóng và hiệu quả.
Bài tập này thường yêu cầu học sinh... (giả sử bài tập liên quan đến bất phương trình bậc nhất một ẩn). Để giải bài tập này, ta cần thực hiện các phép biến đổi tương đương để đưa bất phương trình về dạng đơn giản nhất. Sau đó, tìm ra tập nghiệm của bất phương trình.
Bài tập này có thể liên quan đến việc... (giả sử bài tập liên quan đến ứng dụng của hàm số bậc nhất). Để giải bài tập này, ta cần xây dựng mô hình toán học phù hợp với bài toán thực tế. Sau đó, sử dụng các kiến thức về hàm số bậc nhất để giải quyết bài toán.
Bài tập này thường yêu cầu học sinh... (giả sử bài tập liên quan đến hệ phương trình bậc nhất hai ẩn với ứng dụng thực tế). Để giải bài tập này, ta cần phân tích đề bài để xác định các đại lượng cần tìm và mối quan hệ giữa chúng. Sau đó, xây dựng hệ phương trình và giải hệ phương trình đó.
Trong quá trình giải bài tập, học sinh cần chú ý đến các đơn vị đo lường, các điều kiện của bài toán và các trường hợp đặc biệt. Việc sử dụng máy tính bỏ túi có thể giúp ta thực hiện các phép tính một cách nhanh chóng và chính xác, nhưng không nên quá phụ thuộc vào máy tính mà quên đi việc rèn luyện tư duy và kỹ năng giải toán.
Hy vọng rằng với những hướng dẫn chi tiết và phương pháp giải hiệu quả trên đây, các em học sinh sẽ tự tin giải quyết các bài tập trong mục 2 trang 117, 118, 119 SGK Toán 9 tập 1. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!