Chào mừng các em học sinh đến với bài giải bài tập 5.17 trang 114 SGK Toán 9 tập 1 tại giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và áp dụng vào các bài tập tương tự.
Cho A là một điểm thuộc đường tròn (O), M là một điểm thuộc tiếp tuyến của (O) tại điểm A (M khác A). Đường tròn tâm M bán kính MA cắt (O) tại B (B khác A). Chứng minh rằng MB là một tiếp tuyến của (O).
Đề bài
Cho A là một điểm thuộc đường tròn (O), M là một điểm thuộc tiếp tuyến của (O) tại điểm A (M khác A). Đường tròn tâm M bán kính MA cắt (O) tại B (B khác A). Chứng minh rằng MB là một tiếp tuyến của (O).
Phương pháp giải - Xem chi tiết
+ Chứng minh \(\widehat {MAO} = {90^o}\).
+ Chứng minh \(\Delta AMO = \Delta BMO\left( {c.c.c} \right)\) nên \(\widehat {MAO} = \widehat {MBO} = {90^o}\).
+ Suy ra \(MB \bot BO\) tại B. Mà B thuộc đường tròn (O) nên MB là tiếp tuyến của (O).
Lời giải chi tiết
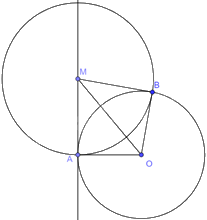
Vì MA là tiếp tuyến của (O) nên \(MA \bot AO\) nên \(\widehat {MAO} = {90^o}\).
Tam giác AMO và tam giác BMO có:
\(OA = OB\) (bán kính (O)), \(MA = MB\) (bán kính (M)), OM chung.
Do đó, \(\Delta AMO = \Delta BMO\left( {c.c.c} \right)\) nên \(\widehat {MAO} = \widehat {MBO} = {90^o}\)
Suy ra \(MB \bot BO\) tại B. Mà B thuộc đường tròn (O) nên MB là tiếp tuyến của (O).
Bài tập 5.17 trang 114 SGK Toán 9 tập 1 yêu cầu chúng ta tìm hiểu về phương pháp tiếp tuyến của một hàm số bậc nhất. Đây là một khái niệm quan trọng trong hình học giải tích, giúp chúng ta xác định được đường thẳng tiếp xúc với đồ thị hàm số tại một điểm cho trước.
Bài tập 5.17 thường có dạng như sau: Cho hàm số y = ax + b. Tìm hệ số a và b sao cho đường thẳng y = ax + b đi qua một điểm cho trước và có hệ số góc thỏa mãn một điều kiện nào đó.
Ví dụ: Cho hàm số y = 2x + b. Tìm b sao cho đường thẳng y = 2x + b đi qua điểm A(1; 3).
Giải:
Ngoài bài tập 5.17, các em có thể gặp các dạng bài tập tương tự như:
Khi giải các bài tập về hàm số bậc nhất và ứng dụng, các em cần lưu ý:
Phương pháp tiếp tuyến có nhiều ứng dụng trong thực tế, chẳng hạn như:
Để củng cố kiến thức về bài tập 5.17, các em có thể tự giải các bài tập sau:
Bài tập 5.17 trang 114 SGK Toán 9 tập 1 là một bài tập quan trọng giúp các em hiểu rõ hơn về phương pháp tiếp tuyến của hàm số bậc nhất. Hy vọng rằng với lời giải chi tiết và các ví dụ minh họa trên, các em sẽ nắm vững kiến thức và tự tin giải các bài tập tương tự.