Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 3 trang 119, 120, 121 sách giáo khoa Toán 9 tập 1.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, nắm vững phương pháp giải và tự tin áp dụng vào các bài tập tương tự. Hãy cùng bắt đầu nhé!
Quay lại hoạt động gấp hình tròn trong Hoạt động 1. Hãy xác định các số đo cung và tỉ số trong các ô ? của bảng dưới đây. Em có nhận xét gì?
Trả lời câu hỏi Luyện tập 3 trang 120 SGK Toán 9 Cùng khám phá
Tính diện tích của hình quạt tròn bán kính 3cm ứng với cung \({210^o}\).
Phương pháp giải:
Công thức tính diện tích hình quạt tròn bán kính R ứng với cung \({n^o}\): \({S_q} = \frac{{\pi {R^2}n}}{{360}}\).
Lời giải chi tiết:
Diện tích của hình quạt tròn bán kính 3cm ứng với cung \({210^o}\) là:
\({S_q} = \frac{{\pi {{.3}^2}.210}}{{360}} = \frac{{21\pi }}{4}\left( {c{m^2}} \right)\).
Trả lời câu hỏi Luyện tập 4 trang 120 SGK Toán 9 Cùng khám phá
Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn đồng tâm có bán kính lần lượt là 5cm và 3cm.
Phương pháp giải:
Diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; R) và (O; r) (với \(r < R\)): \({S_{vk}} = \pi \left( {{R^2} - {r^2}} \right)\).
Lời giải chi tiết:
Diện tích hình vành khuyên giới hạn bởi hai đường tròn đồng tâm có bán kính lần lượt là 5cm và 3cm là:
\({S_{vk}} = \pi \left( {{5^2} - {3^2}} \right) = 16\pi \left( {c{m^2}} \right)\).
Trả lời câu hỏi Hoạt động 4 trang 119SGK Toán 9 Cùng khám phá
Quay lại hoạt động gấp hình tròn trong Hoạt động 1.
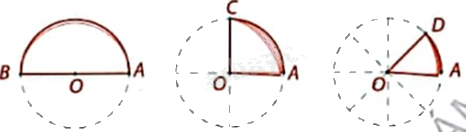
Hãy xác định các số đo cung và tỉ số trong các ô ? của bảng dưới đây. Em có nhận xét gì?

Phương pháp giải:
+ Số đo các cung AB, AC, AD lần lượt có số đo là \({180^o}\), \({90^o}\), \({45^o}\).
+ Tỉ số của số đo cung và \({360^o}\) bằng thương giữa số đo cung tương ứng và \({360^o}\).
+ Nhận xét: Tỉ số của số đo cung và \({360^o}\) bằng tỉ số của diện tích hình quạt tròn giới hạn bởi cung và diện tích hình tròn.
Lời giải chi tiết:
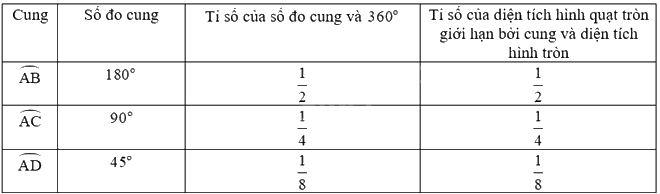
Nhận xét: Tỉ số của số đo cung và \({360^o}\) bằng tỉ số của diện tích hình quạt tròn giới hạn bởi cung và diện tích hình tròn.
Trả lời câu hỏi Luyện tập 3 trang 120 SGK Toán 9 Cùng khám phá
Tính diện tích của hình quạt tròn bán kính 3cm ứng với cung \({210^o}\).
Phương pháp giải:
Công thức tính diện tích hình quạt tròn bán kính R ứng với cung \({n^o}\): \({S_q} = \frac{{\pi {R^2}n}}{{360}}\).
Lời giải chi tiết:
Diện tích của hình quạt tròn bán kính 3cm ứng với cung \({210^o}\) là:
\({S_q} = \frac{{\pi {{.3}^2}.210}}{{360}} = \frac{{21\pi }}{4}\left( {c{m^2}} \right)\).
Trả lời câu hỏi Luyện tập 4 trang 120 SGK Toán 9 Cùng khám phá
Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn đồng tâm có bán kính lần lượt là 5cm và 3cm.
Phương pháp giải:
Diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; R) và (O; r) (với \(r < R\)): \({S_{vk}} = \pi \left( {{R^2} - {r^2}} \right)\).
Lời giải chi tiết:
Diện tích hình vành khuyên giới hạn bởi hai đường tròn đồng tâm có bán kính lần lượt là 5cm và 3cm là:
\({S_{vk}} = \pi \left( {{5^2} - {3^2}} \right) = 16\pi \left( {c{m^2}} \right)\).
Trả lời câu hỏi Vận dụng trang 121SGK Toán 9 Cùng khám phá
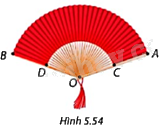
Trong Hình 5.54, chiếc quạt có dạng một hình quạt tròn tâm O cung AB, bán kính \(OA = OB = 20cm\). Giấy được dán trong phần giới hạn bởi cung AB, cung CD, đoạn thẳng AC và BD với \(OC = OD = 10cm\). Biết khi mở rộng tối đa, hai nan quạt ngoài cùng tạo thành một góc \(\widehat {AOB} = {140^o}\). Tính chu vi và diện tích mảnh giấy để dán một mặt quạt (diện tích mép không đáng kể).
Phương pháp giải:
Công thức tính độ dài cung \({n^o}\) của đường tròn bán kính R: \(l = \frac{{\pi Rn}}{{180}}\).
Công thức tính diện tích hình quạt tròn bán kính R ứng với cung \({n^o}\): \({S_q} = \frac{{\pi {R^2}n}}{{360}}\).
Lời giải chi tiết:
Ta có: \(BD = AC = OB - OD = 20 - 10 = 10cm\).
Diện tích hình quạt tâm O, cung AB là:
\({S_{AOB}} = \frac{{\pi {{.20}^2}.140}}{{360}} = \frac{{1400}}{9}\pi \left( {c{m^2}} \right)\).
Diện tích hình quạt tâm O, cung CD là:
\({S_{COD}} = \frac{{\pi {{.10}^2}.140}}{{360}} = \frac{{350}}{9}\pi \left( {c{m^2}} \right)\).
Diện tích mảnh giấy để dán một mặt quạt là:
\(S = {S_{AOB}} - {S_{COD}} = \frac{{1400}}{9}\pi - \frac{{350}}{9}\pi = \frac{{350}}{3}\pi \left( {c{m^2}} \right)\).
Độ dài cung AB là:
\({l_{AB}} = \frac{{\pi .20.140}}{{180}} = \frac{{140}}{9}\pi \left( {cm} \right)\).
Độ dài cung CD là:
\({l_{CD}} = \frac{{\pi .10.140}}{{180}} = \frac{{70}}{9}\pi \left( {cm} \right)\).
Chu vi mảnh giấy để dán một mặt quạt là:
\(AC + BD + {l_{AB}} + {l_{CD}} = 10 + 10 + \frac{{140\pi }}{9} + \frac{{70\pi }}{9} = 20 + \frac{{70\pi }}{3}\left( {cm} \right)\)
Trả lời câu hỏi Vận dụng trang 121SGK Toán 9 Cùng khám phá
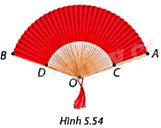
Trong Hình 5.54, chiếc quạt có dạng một hình quạt tròn tâm O cung AB, bán kính \(OA = OB = 20cm\). Giấy được dán trong phần giới hạn bởi cung AB, cung CD, đoạn thẳng AC và BD với \(OC = OD = 10cm\). Biết khi mở rộng tối đa, hai nan quạt ngoài cùng tạo thành một góc \(\widehat {AOB} = {140^o}\). Tính chu vi và diện tích mảnh giấy để dán một mặt quạt (diện tích mép không đáng kể).
Phương pháp giải:
Công thức tính độ dài cung \({n^o}\) của đường tròn bán kính R: \(l = \frac{{\pi Rn}}{{180}}\).
Công thức tính diện tích hình quạt tròn bán kính R ứng với cung \({n^o}\): \({S_q} = \frac{{\pi {R^2}n}}{{360}}\).
Lời giải chi tiết:
Ta có: \(BD = AC = OB - OD = 20 - 10 = 10cm\).
Diện tích hình quạt tâm O, cung AB là:
\({S_{AOB}} = \frac{{\pi {{.20}^2}.140}}{{360}} = \frac{{1400}}{9}\pi \left( {c{m^2}} \right)\).
Diện tích hình quạt tâm O, cung CD là:
\({S_{COD}} = \frac{{\pi {{.10}^2}.140}}{{360}} = \frac{{350}}{9}\pi \left( {c{m^2}} \right)\).
Diện tích mảnh giấy để dán một mặt quạt là:
\(S = {S_{AOB}} - {S_{COD}} = \frac{{1400}}{9}\pi - \frac{{350}}{9}\pi = \frac{{350}}{3}\pi \left( {c{m^2}} \right)\).
Độ dài cung AB là:
\({l_{AB}} = \frac{{\pi .20.140}}{{180}} = \frac{{140}}{9}\pi \left( {cm} \right)\).
Độ dài cung CD là:
\({l_{CD}} = \frac{{\pi .10.140}}{{180}} = \frac{{70}}{9}\pi \left( {cm} \right)\).
Chu vi mảnh giấy để dán một mặt quạt là:
\(AC + BD + {l_{AB}} + {l_{CD}} = 10 + 10 + \frac{{140\pi }}{9} + \frac{{70\pi }}{9} = 20 + \frac{{70\pi }}{3}\left( {cm} \right)\)
Trả lời câu hỏi Hoạt động 4 trang 119SGK Toán 9 Cùng khám phá
Quay lại hoạt động gấp hình tròn trong Hoạt động 1.
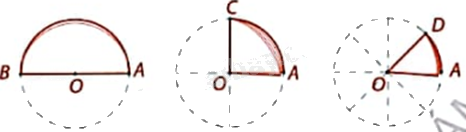
Hãy xác định các số đo cung và tỉ số trong các ô ? của bảng dưới đây. Em có nhận xét gì?

Phương pháp giải:
+ Số đo các cung AB, AC, AD lần lượt có số đo là \({180^o}\), \({90^o}\), \({45^o}\).
+ Tỉ số của số đo cung và \({360^o}\) bằng thương giữa số đo cung tương ứng và \({360^o}\).
+ Nhận xét: Tỉ số của số đo cung và \({360^o}\) bằng tỉ số của diện tích hình quạt tròn giới hạn bởi cung và diện tích hình tròn.
Lời giải chi tiết:
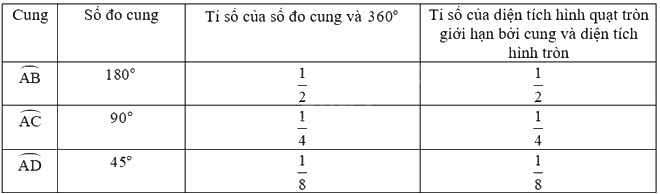
Nhận xét: Tỉ số của số đo cung và \({360^o}\) bằng tỉ số của diện tích hình quạt tròn giới hạn bởi cung và diện tích hình tròn.
Mục 3 của SGK Toán 9 tập 1 thường tập trung vào một chủ đề cụ thể trong hình học hoặc đại số. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững kiến thức lý thuyết, các định nghĩa, định lý và công thức liên quan. Việc hiểu rõ bản chất của bài toán cũng rất quan trọng để lựa chọn phương pháp giải phù hợp.
Bài tập này thường yêu cầu học sinh vận dụng kiến thức về một khái niệm hoặc định lý đã học để chứng minh một đẳng thức, giải một phương trình hoặc tìm một giá trị cụ thể. Ví dụ, bài tập có thể yêu cầu chứng minh hai tam giác bằng nhau theo một trường hợp bằng nhau đã biết.
Hướng dẫn giải:
Bài tập này có thể yêu cầu học sinh giải một bài toán thực tế liên quan đến kiến thức đã học. Ví dụ, bài tập có thể yêu cầu tính chiều cao của một tòa nhà dựa vào góc nâng và khoảng cách từ một điểm quan sát đến chân tòa nhà.
Hướng dẫn giải:
Bài tập này có thể là một bài tập tổng hợp, yêu cầu học sinh vận dụng nhiều kiến thức và kỹ năng khác nhau để giải quyết. Ví dụ, bài tập có thể yêu cầu chứng minh một tính chất hình học phức tạp hoặc giải một hệ phương trình bậc hai.
Hướng dẫn giải:
Đối với các bài tập tổng hợp, học sinh cần có một kế hoạch giải cụ thể, chia nhỏ bài toán thành các bước nhỏ hơn và giải quyết từng bước một. Việc sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm vẽ hình cũng có thể giúp ích.
Trong mục 3, học sinh có thể gặp các dạng bài tập sau:
Để học tập môn Toán hiệu quả, học sinh nên:
Hy vọng rằng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải quyết các bài tập trong mục 3 trang 119, 120, 121 SGK Toán 9 tập 1. Chúc các em học tập tốt và đạt kết quả cao!
| Bài tập | Nội dung chính | Mức độ khó |
|---|---|---|
| Bài 1 | Chứng minh đẳng thức | Dễ |
| Bài 2 | Giải bài toán thực tế | Trung bình |
| Bài 3 | Tổng hợp kiến thức | Khó |