Chào mừng các em học sinh đến với bài giải bài tập 9.14 trang 84 SGK Toán 9 tập 2 tại giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
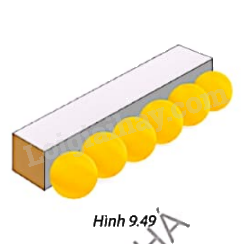
Một công ty thiết kế mẫu hộp làm từ bìa mỏng dạng hình hộp chữ nhật để đóng gói 6 quả bóng bàn có thông số kĩ thuật \(\phi \)40 (đường kính bóng là 40 mm) (Hình 9.49). a) Tính diện tích xung quanh của hộp, biết rằng đáy hộp là hình vuông cạnh 40 mm và chiều cao của hộp vừa đủ để xếp khít 6 quả bóng bàn. b) Tính thể tích phần không gian trống của hộp khi chứa 6 quả bóng bàn.
Đề bài
Một công ty thiết kế mẫu hộp làm từ bìa mỏng dạng hình hộp chữ nhật để đóng gói 6 quả bóng bàn có thông số kĩ thuật \(\phi \)40 (đường kính bóng là 40 mm) (Hình 9.49).
a) Tính diện tích xung quanh của hộp, biết rằng đáy hộp là hình vuông cạnh 40 mm và chiều cao của hộp vừa đủ để xếp khít 6 quả bóng bàn.
b) Tính thể tích phần không gian trống của hộp khi chứa 6 quả bóng bàn.
Phương pháp giải - Xem chi tiết
Diện tích xung quanh của hình hộp chữ nhật: \({S_{xq}} = P.h\) (với P là chu vi đáy, h là chiều cao)
Thể tích hình hộp chữ nhật là: V = Sđáy . h.
Thể tích của hình cầu là: \(V = \frac{4}{3}\pi {R^3}\)(với R là bán kính hình cầu)
Lời giải chi tiết
a) Chiều cao của hộp là:
40.6 = 240 mm
Chu vi đáy hình vuông là:
4.40 = 160 mm
Diện tích xung quanh của hình hộp chữ nhật:
\({S_{xq}} = P.h = \)160.240 = 38400 (mm2).
b) Thể tích hình hộp chữ nhật là:
V = Sđáy . h = 40.40.240 = 384000 (mm3)
Thể tích 6 quả bóng là:
6. \(\frac{4}{3}\pi {R^3} = 6.\frac{4}{3}\pi {.20^3} \approx 201062\) (mm3)
Vậy thể tích phần không gian trống của hộp là:
384000 – 201061 = 182939 mm3.
Bài tập 9.14 trang 84 SGK Toán 9 tập 2 yêu cầu chúng ta xét hàm số y = (m-1)x + 3. Để hàm số này là hàm số bậc nhất, điều kiện cần và đủ là hệ số của x khác 0, tức là m-1 ≠ 0, suy ra m ≠ 1.
Như đã đề cập ở trên, để y = (m-1)x + 3 là hàm số bậc nhất, ta cần m ≠ 1. Điều này đảm bảo rằng hàm số có dạng y = ax + b, trong đó a là hệ số góc và b là tung độ gốc.
Hàm số bậc nhất y = ax + b đồng biến khi và chỉ khi a > 0. Trong trường hợp này, a = m-1. Do đó, để hàm số y = (m-1)x + 3 đồng biến, ta cần m-1 > 0, suy ra m > 1.
Hàm số bậc nhất y = ax + b nghịch biến khi và chỉ khi a < 0. Trong trường hợp này, a = m-1. Do đó, để hàm số y = (m-1)x + 3 nghịch biến, ta cần m-1 < 0, suy ra m < 1.
Để hiểu rõ hơn về bài toán này, chúng ta hãy xét một vài ví dụ cụ thể:
Ngoài bài tập 9.14, còn rất nhiều bài tập tương tự liên quan đến hàm số bậc nhất. Các em có thể tham khảo các bài tập sau:
Để giải tốt các bài tập về hàm số bậc nhất, các em cần nắm vững các khái niệm cơ bản như:
Ngoài ra, các em cũng nên luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Bài tập 9.14 trang 84 SGK Toán 9 tập 2 là một bài tập quan trọng giúp các em hiểu rõ hơn về hàm số bậc nhất. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em sẽ nắm vững kiến thức và kỹ năng giải bài tập này một cách hiệu quả. Chúc các em học tốt!