Chào mừng các em học sinh đến với bài giải bài tập 4.13 trang 87 SGK Toán 9 tập 1 của giaitoan.edu.vn. Bài tập này thuộc chương Hàm số bậc nhất và ứng dụng. Chúng tôi sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
Giaitoan.edu.vn là nền tảng học toán online uy tín, cung cấp đầy đủ các bài giải SGK Toán 9, bài tập trắc nghiệm, và các tài liệu học tập hữu ích khác.
Cánh tay rô-bốt đặt trên mặt đất và có vị trí như Hình 4.28. Tính độ cao của điểm A trên đầu cánh tay rô-bốt so với mặt đất.
Đề bài
Cánh tay rô-bốt đặt trên mặt đất và có vị trí như Hình 4.28. Tính độ cao của điểm A trên đầu cánh tay rô-bốt so với mặt đất.
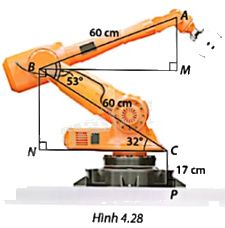
Phương pháp giải - Xem chi tiết
Vì BM//NC (cùng vuông góc với BN) nên \(\widehat {CBM} = \widehat {BCN} = {32^o}\) (hai góc so le trong).
Ta có: \(\widehat {ABM} = \widehat {CBA} - \widehat {BCM}\).
Tam giác NBC vuông tại N nên \(NB = BC.\sin NCB\).
Tam giác ABM vuông tại M nên \(AM = AB.\sin ABM\).
Vậy độ cao của điểm A trên đầu cánh tay rô- bốt so với mặt đất là: \(h = CP + BN + AM\).
Lời giải chi tiết
Vì BM//NC (cùng vuông góc với BN) nên \(\widehat {CBM} = \widehat {BCN} = {32^o}\) (hai góc so le trong).
Ta có: \(\widehat {ABM} = \widehat {CBA} - \widehat {BCM} = {53^o} - {32^o} = {21^o}\).
Tam giác NBC vuông tại N nên
\(NB = BC.\sin NCB = 60.\sin {32^o} \approx 31,8\left( cm \right)\).
Tam giác ABM vuông tại M nên
\(AM = AB.\sin ABM = 60.\sin {21^o} \approx 21,5\left( cm \right)\).
Vậy độ cao của điểm A trên đầu cánh tay rô-bốt so với mặt đất là: \(h = CP + BN + AM \approx 17 + 31,8 + 21,5 \approx 70,3\left( cm \right)\)
Bài tập 4.13 trang 87 SGK Toán 9 tập 1 yêu cầu chúng ta giải một bài toán liên quan đến hàm số bậc nhất. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về hàm số bậc nhất, bao gồm định nghĩa, dạng tổng quát, và các tính chất của hàm số.
Hàm số bậc nhất có dạng y = ax + b (với a ≠ 0).
Để xác định một hàm số bậc nhất, chúng ta cần biết hai điểm thuộc đồ thị hàm số hoặc biết hệ số góc và một điểm thuộc đồ thị hàm số.
Trước khi đi vào giải bài tập cụ thể, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Bài toán thường yêu cầu chúng ta:
(Ở đây sẽ là lời giải chi tiết cho bài tập 4.13, bao gồm các bước giải, giải thích rõ ràng và các lưu ý quan trọng. Ví dụ, nếu bài toán yêu cầu tìm hàm số bậc nhất đi qua hai điểm A(x1, y1) và B(x2, y2), lời giải sẽ trình bày cách tính hệ số góc a và tung độ gốc b.)
Để giúp các em hiểu rõ hơn về cách giải bài tập hàm số bậc nhất, chúng ta sẽ xem xét một số ví dụ minh họa và bài tập tương tự:
Hàm số bậc nhất có rất nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng với bài giải chi tiết và các ví dụ minh họa trên, các em học sinh đã nắm vững cách giải bài tập 4.13 trang 87 SGK Toán 9 tập 1. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!
| Công thức quan trọng | Giải thích |
|---|---|
| Hệ số góc (a) | Độ dốc của đường thẳng |
| Tung độ gốc (b) | Giao điểm với trục Oy |