Chào mừng các em học sinh đến với bài giải chi tiết mục 4 trang 35 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em lời giải đầy đủ, dễ hiểu, giúp các em hiểu rõ hơn về kiến thức và phương pháp giải bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ các em trong quá trình học tập môn Toán.
a) Trong một mùa thi đấu giải vô địch bóng đá quốc gia, đội A ghi được ít bàn thắng hơn đội B, đội B lại ghi được ít bàn thắng hơn đội C. Gọi \(a,b,c\) lần lượt là số bàn thắng của đội A, B, C. Viết các bất đẳng thức biểu thị quan hệ thứ tự giữa \(a\) và \(b\), giữa \(b\) và \(c\). b) Hình 2.2 cho biết biểu diễn của \(a\) trên trục số. Hãy biểu diễn \(b\) và \(c\) trên trục số. So sánh số bàn thắng của các đội A và C.
Trả lời câu hỏi Luyện tập 5 trang 35 SGK Toán 9 Cùng khám phá
Cho \(x \ge y\). Chứng minh rằng \(0,8x + 1 \ge 0,8y - 1\).
Phương pháp giải:
Dựa vào tính chất bắc cầu của thứ tự để giải bài toán.
Lời giải chi tiết:
Theo giả thiết thì \(x \ge y\). Nhân \(0,8\) vào hai vế của bất đẳng thức, ta có \(0,8x \ge 0,8y\). (1)
Cộng 1 vào hai vế của bất đẳng thức (1), ta được \(0,8x + 1 \ge 0,8y + 1\). (2)
Mặt khác, vì \(1 > - 1\) nên \(0,8y + 1 > 0,8y - 1\). (3)
Từ (2) và (3), sử dụng tính chất bắc cầu, suy ra \(0,8x + 1 \ge 0,8y - 1\).
Trả lời câu hỏi Hoạt động 5 trang 35 SGK Toán 9 Cùng khám phá
a) Trong một mùa thi đấu giải vô địch bóng đá quốc gia, đội A ghi được ít bàn thắng hơn đội B, đội B lại ghi được ít bàn thắng hơn đội C. Gọi \(a,b,c\) lần lượt là số bàn thắng của đội A, B, C. Viết các bất đẳng thức biểu thị quan hệ thứ tự giữa \(a\) và \(b\), giữa \(b\) và \(c\).
b) Hình 2.2 cho biết biểu diễn của \(a\) trên trục số.
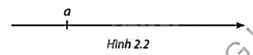
Hãy biểu diễn \(b\) và \(c\) trên trục số. So sánh số bàn thắng của các đội A và C.
Phương pháp giải:
Dựa vào định nghĩa bất đẳng thức để giải bài toán.
Lời giải chi tiết:
a) Bất đẳng thức biểu thị quan hệ thứ tự giữa \(a\) và \(b\) là: \(a < b\).
Bất đẳng thức biểu thị quan hệ thứ tự giữa \(b\) và \(c\) là: \(b < c\).
b) Biểu diễn \(b\) và \(c\) trên trục số
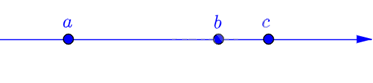
So sánh só bàn thắng của các đội A và C là: \(a < c\).
Trả lời câu hỏi Luyện tập 5 trang 35 SGK Toán 9 Cùng khám phá
Cho \(x \ge y\). Chứng minh rằng \(0,8x + 1 \ge 0,8y - 1\).
Phương pháp giải:
Dựa vào tính chất bắc cầu của thứ tự để giải bài toán.
Lời giải chi tiết:
Theo giả thiết thì \(x \ge y\). Nhân \(0,8\) vào hai vế của bất đẳng thức, ta có \(0,8x \ge 0,8y\). (1)
Cộng 1 vào hai vế của bất đẳng thức (1), ta được \(0,8x + 1 \ge 0,8y + 1\). (2)
Mặt khác, vì \(1 > - 1\) nên \(0,8y + 1 > 0,8y - 1\). (3)
Từ (2) và (3), sử dụng tính chất bắc cầu, suy ra \(0,8x + 1 \ge 0,8y - 1\).
Trả lời câu hỏi Hoạt động 5 trang 35 SGK Toán 9 Cùng khám phá
a) Trong một mùa thi đấu giải vô địch bóng đá quốc gia, đội A ghi được ít bàn thắng hơn đội B, đội B lại ghi được ít bàn thắng hơn đội C. Gọi \(a,b,c\) lần lượt là số bàn thắng của đội A, B, C. Viết các bất đẳng thức biểu thị quan hệ thứ tự giữa \(a\) và \(b\), giữa \(b\) và \(c\).
b) Hình 2.2 cho biết biểu diễn của \(a\) trên trục số.
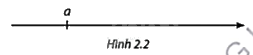
Hãy biểu diễn \(b\) và \(c\) trên trục số. So sánh số bàn thắng của các đội A và C.
Phương pháp giải:
Dựa vào định nghĩa bất đẳng thức để giải bài toán.
Lời giải chi tiết:
a) Bất đẳng thức biểu thị quan hệ thứ tự giữa \(a\) và \(b\) là: \(a < b\).
Bất đẳng thức biểu thị quan hệ thứ tự giữa \(b\) và \(c\) là: \(b < c\).
b) Biểu diễn \(b\) và \(c\) trên trục số
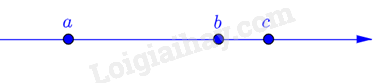
So sánh só bàn thắng của các đội A và C là: \(a < c\).
Mục 4 trang 35 SGK Toán 9 tập 1 thường xoay quanh các bài tập về hàm số bậc nhất, bao gồm việc xác định hàm số, vẽ đồ thị hàm số, và ứng dụng hàm số vào giải quyết các bài toán thực tế. Việc nắm vững kiến thức về hàm số bậc nhất là nền tảng quan trọng cho các chương trình học Toán ở các lớp trên.
Để giúp các em hiểu rõ hơn về nội dung bài tập, chúng ta sẽ đi vào phân tích từng bài tập cụ thể:
Bài tập này yêu cầu học sinh xác định các hệ số a và b trong hàm số y = ax + b dựa vào các thông tin cho trước, chẳng hạn như đồ thị hàm số hoặc các điểm thuộc đồ thị hàm số. Để giải bài tập này, học sinh cần nắm vững các khái niệm về hệ số góc và tung độ gốc.
Bài tập này yêu cầu học sinh vẽ đồ thị hàm số y = ax + b. Để vẽ đồ thị hàm số, học sinh cần xác định ít nhất hai điểm thuộc đồ thị hàm số. Sau đó, học sinh nối hai điểm này lại với nhau để được đồ thị hàm số.
Bài tập này yêu cầu học sinh sử dụng hàm số bậc nhất để giải quyết các bài toán thực tế, chẳng hạn như tính quãng đường đi được của một vật chuyển động đều, tính tiền lương của một công nhân dựa vào số sản phẩm làm được, hoặc tính giá trị của một hàng hóa dựa vào số lượng mua.
Để giải bài tập hàm số bậc nhất một cách hiệu quả, học sinh cần nắm vững các phương pháp sau:
Ví dụ 1: Cho hàm số y = 2x + 1. Hãy xác định hệ số a và b.
Giải: Trong hàm số y = 2x + 1, hệ số a là 2 và hệ số b là 1.
Ví dụ 2: Vẽ đồ thị hàm số y = -x + 2.
Giải: Để vẽ đồ thị hàm số y = -x + 2, ta xác định hai điểm thuộc đồ thị hàm số. Ví dụ, khi x = 0 thì y = 2, và khi x = 2 thì y = 0. Nối hai điểm (0, 2) và (2, 0) lại với nhau, ta được đồ thị hàm số.
Để củng cố kiến thức về hàm số bậc nhất, các em có thể làm thêm các bài tập sau:
Hy vọng rằng bài giải chi tiết mục 4 trang 35 SGK Toán 9 tập 1 trên giaitoan.edu.vn sẽ giúp các em hiểu rõ hơn về kiến thức và phương pháp giải bài tập hàm số bậc nhất. Chúc các em học tập tốt!
| Bài tập | Nội dung |
|---|---|
| Bài 1 | Xác định hàm số bậc nhất |
| Bài 2 | Vẽ đồ thị hàm số bậc nhất |
| Bài 3 | Ứng dụng hàm số bậc nhất |