Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 tại giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 105, 106, 107 của sách giáo khoa Toán 9 tập 2.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong các kỳ thi sắp tới.
Dưới đây là hai bảng thống kê kết quả kiểm tra cân nặng của cá nuôi ở hai ao với hai điều kiện chăm sóc A, B: Cá được xem là đảm bảo chất lượng nếu đạt khối lượng không dưới 700 g. Vậy cá nuôi ở diều kiện A hay B cho kết quả tốt hơn? Để trả lời câu hỏi này, bạn Nam phân tích: Đối chiếu hai bảng thì thấy: • Loại 700 g: nuôi ở điều kiện A đạt 30 con, nuôi ở điều kiện B đạt ít hơn (25 con); • Loại 800 g: nuôi ở điều kiện A đạt 80 con, nuôi ở điều kiện B đạt ít hơn (75 con); • Loại 900 g: nu
Trả lời câu hỏi Hoạt động 1 trang 105SGK Toán 9 Cùng khám phá
Dưới đây là hai bảng thống kê kết quả kiểm tra cân nặng của cá nuôi ở hai ao với hai điều kiện chăm sóc A, B: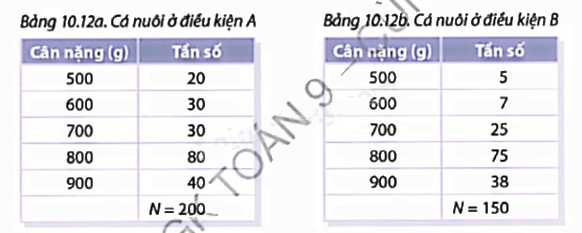 
Cá được xem là đảm bảo chất lượng nếu đạt khối lượng không dưới 700 g. Vậy cá nuôi ở diều kiện A hay B cho kết quả tốt hơn?Để trả lời câu hỏi này, bạn Nam phân tích: Đối chiếu hai bảng thì thấy:• Loại 700 g: nuôi ở điều kiện A đạt 30 con, nuôi ở điều kiện B đạt ít hơn (25 con);• Loại 800 g: nuôi ở điều kiện A đạt 80 con, nuôi ở điều kiện B đạt ít hơn (75 con);• Loại 900 g: nuôi ở điều kiện A đạt 40 con, nuôi ở điều kiện B đạt ít hơn (38 con).Suy ra cá nuôi ở điều kiện A cho kết quả tốt hơn.Em có tán thành cách phân tích của Nam không? Vì sao? Nếu không tán thành thì hãy thử đề xuất một cách phân tích khác.
Phương pháp giải:
Đọc kĩ dữ liệu đề bài và trả lời câu hỏi.
Lời giải chi tiết:
Em không tán thành cách phân tích của Nam vì còn cả loại cá 500 g và 600 g cần xét đến. Nên tính tỉ lệ từng loại các rồi so sánh.
Trả lời câu hỏi Luyện tập 2 trang 108SGK Toán 9 Cùng khám phá
Trở lại với hai mẫu số liệu cho ở các Bảng 10.12a và Bảng 10.12b trong Hoạt động 1.
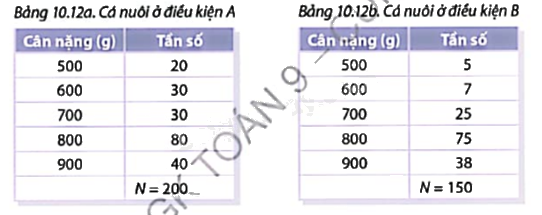
a) Lập bảng tần số tương đối ứng với hai bảng dữ liệu đã cho.
b) Nếu số các bắt lên để kiểm tra đại diện được cho cá trong mỗi ao thì có thể dự kiến số cá đạt yêu cầu trong mỗi ao là bao nhiêu phần trăm? Giữa hai điều kiện chăm sóc A và B, có thể nói là điều kiện nào đạt hiệu quả tốt hơn?
Phương pháp giải:
Công thức tính tần tương đối: \({f_i} = \frac{{{n_i}}}{N}.100\% \) và lập bảng tần số tương đối rồi trả lời câu hỏi.
Lời giải chi tiết:
a) Bảng 10.12a
Bảng 10.12b
b) Dự kiến số cá đạt yêu cầu bắt lên trong ao Bảng 10.12a là 40% + 20% = 60%.
Dự kiến số cá đạt yêu cầu bắt lên trong ao Bảng 10.12b là 50% + 25,3% = 75,3%.
Vậy giữa hai điều kiện chăm sóc A và B, có thể nói là điều kiện chăm sóc B đạt hiệu quả tốt hơn.
Trả lời câu hỏi Luyện tập 1 trang 107 SGK Toán 9 Cùng khám phá
a) Điểm kiểm tra môn Ngữ Văn của học sinh lớp 9A1 được thống kê trong Bảng 10.14a.
Lập bảng tần số tươg đối của bảng điểm đã cho (làm tròn kết quả đến hàng phần trăm).
b) Cũng với bài kiểm tra này, căn cứ vào bảng điểm của lớp 9A2, bạn Tùng lập bảng tần số tương đối dưới đây:
Hãy kiểm tra xem bảng của bạn Tùng lập có chính xác không. Giải thích cách kiểm tra của em.
Phương pháp giải:
Công thức tính tần tương đối: \({f_i} = \frac{{{n_i}}}{N}.100\% \).
Lời giải chi tiết:
a)
b) Ta có tổng phần trăm của tần số tương đối là 100%.
Mà tổng tần số tương đối điểm của lớp 9A2 bạn Tùng lập ra có:
11,9% + 31,1% + 26,2% + 19,1% + 11,9% = 100,2%.
Vậy bảng của bạn Tùng lập không chính xác.
Trả lời câu hỏi Hoạt động 1 trang 105SGK Toán 9 Cùng khám phá
Dưới đây là hai bảng thống kê kết quả kiểm tra cân nặng của cá nuôi ở hai ao với hai điều kiện chăm sóc A, B: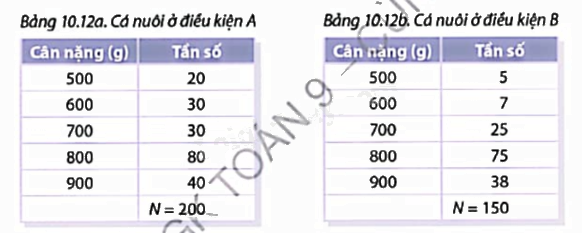 
Cá được xem là đảm bảo chất lượng nếu đạt khối lượng không dưới 700 g. Vậy cá nuôi ở diều kiện A hay B cho kết quả tốt hơn?Để trả lời câu hỏi này, bạn Nam phân tích: Đối chiếu hai bảng thì thấy:• Loại 700 g: nuôi ở điều kiện A đạt 30 con, nuôi ở điều kiện B đạt ít hơn (25 con);• Loại 800 g: nuôi ở điều kiện A đạt 80 con, nuôi ở điều kiện B đạt ít hơn (75 con);• Loại 900 g: nuôi ở điều kiện A đạt 40 con, nuôi ở điều kiện B đạt ít hơn (38 con).Suy ra cá nuôi ở điều kiện A cho kết quả tốt hơn.Em có tán thành cách phân tích của Nam không? Vì sao? Nếu không tán thành thì hãy thử đề xuất một cách phân tích khác.
Phương pháp giải:
Đọc kĩ dữ liệu đề bài và trả lời câu hỏi.
Lời giải chi tiết:
Em không tán thành cách phân tích của Nam vì còn cả loại cá 500 g và 600 g cần xét đến. Nên tính tỉ lệ từng loại các rồi so sánh.
Trả lời câu hỏi Luyện tập 1 trang 107 SGK Toán 9 Cùng khám phá
a) Điểm kiểm tra môn Ngữ Văn của học sinh lớp 9A1 được thống kê trong Bảng 10.14a.
Lập bảng tần số tươg đối của bảng điểm đã cho (làm tròn kết quả đến hàng phần trăm).
b) Cũng với bài kiểm tra này, căn cứ vào bảng điểm của lớp 9A2, bạn Tùng lập bảng tần số tương đối dưới đây:
Hãy kiểm tra xem bảng của bạn Tùng lập có chính xác không. Giải thích cách kiểm tra của em.
Phương pháp giải:
Công thức tính tần tương đối: \({f_i} = \frac{{{n_i}}}{N}.100\% \).
Lời giải chi tiết:
a)
b) Ta có tổng phần trăm của tần số tương đối là 100%.
Mà tổng tần số tương đối điểm của lớp 9A2 bạn Tùng lập ra có:
11,9% + 31,1% + 26,2% + 19,1% + 11,9% = 100,2%.
Vậy bảng của bạn Tùng lập không chính xác.
Trả lời câu hỏi Luyện tập 2 trang 108SGK Toán 9 Cùng khám phá
Trở lại với hai mẫu số liệu cho ở các Bảng 10.12a và Bảng 10.12b trong Hoạt động 1.
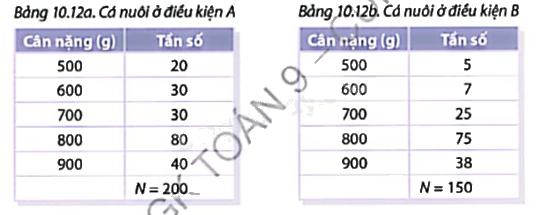
a) Lập bảng tần số tương đối ứng với hai bảng dữ liệu đã cho.
b) Nếu số các bắt lên để kiểm tra đại diện được cho cá trong mỗi ao thì có thể dự kiến số cá đạt yêu cầu trong mỗi ao là bao nhiêu phần trăm? Giữa hai điều kiện chăm sóc A và B, có thể nói là điều kiện nào đạt hiệu quả tốt hơn?
Phương pháp giải:
Công thức tính tần tương đối: \({f_i} = \frac{{{n_i}}}{N}.100\% \) và lập bảng tần số tương đối rồi trả lời câu hỏi.
Lời giải chi tiết:
a) Bảng 10.12a
Bảng 10.12b
b) Dự kiến số cá đạt yêu cầu bắt lên trong ao Bảng 10.12a là 40% + 20% = 60%.
Dự kiến số cá đạt yêu cầu bắt lên trong ao Bảng 10.12b là 50% + 25,3% = 75,3%.
Vậy giữa hai điều kiện chăm sóc A và B, có thể nói là điều kiện chăm sóc B đạt hiệu quả tốt hơn.
Mục 1 của chương trình Toán 9 tập 2 thường tập trung vào các chủ đề quan trọng như hàm số bậc nhất, hệ số góc, và ứng dụng của hàm số trong việc giải quyết các bài toán thực tế. Việc nắm vững kiến thức trong mục này là nền tảng cho việc học các chương tiếp theo và chuẩn bị cho kỳ thi cuối năm.
Bài tập này yêu cầu học sinh xác định các hệ số a và b trong hàm số y = ax + b dựa trên các thông tin cho trước, chẳng hạn như đồ thị hàm số hoặc các điểm thuộc đồ thị. Để giải bài tập này, học sinh cần nắm vững định nghĩa của hàm số bậc nhất và cách xác định hệ số góc.
Bài tập này yêu cầu học sinh tính hệ số góc của đường thẳng dựa trên các thông tin cho trước, chẳng hạn như hai điểm thuộc đường thẳng hoặc phương trình đường thẳng. Để giải bài tập này, học sinh cần nắm vững công thức tính hệ số góc và cách áp dụng công thức vào các bài toán cụ thể.
Bài tập này yêu cầu học sinh vẽ đồ thị hàm số bậc nhất dựa trên phương trình hàm số. Để giải bài tập này, học sinh cần xác định các điểm thuộc đồ thị hàm số và nối các điểm đó lại với nhau để tạo thành đường thẳng.
Bài tập này yêu cầu học sinh sử dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế, chẳng hạn như tính quãng đường đi được của một vật chuyển động đều hoặc tính tiền lương của một công nhân dựa trên số sản phẩm làm được. Để giải bài tập này, học sinh cần phân tích bài toán, xây dựng phương trình hàm số và giải phương trình đó.
Ví dụ: Cho hàm số y = 2x - 1. Hãy xác định hệ số góc của hàm số.
Giải: Hàm số y = 2x - 1 là hàm số bậc nhất với hệ số a = 2 và b = -1. Vậy hệ số góc của hàm số là 2.
Hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh đã có thể tự tin giải các bài tập trong mục 1 trang 105, 106, 107 SGK Toán 9 tập 2. Chúc các em học tập tốt và đạt kết quả cao trong các kỳ thi sắp tới!
