Chào mừng các em học sinh đến với bài giải bài tập 7.10 trang 38 SGK Toán 9 tập 2 trên giaitoan.edu.vn. Bài tập này thuộc chương Hàm số bậc nhất và là một phần quan trọng trong việc củng cố kiến thức về hàm số.
Chúng tôi sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và áp dụng vào các bài tập tương tự.
Cho đường tròn tâm O có bán kính R = 5 cm. a) Tính độ dài cạnh của hình vuông nội tiếp trong (O). b) Một hình chữ nhật nội tiếp (O) có chu vi 28 cm. Tính chiều dài và chiều rộng của hình chữ nhật đó.
Đề bài
Cho đường tròn tâm O có bán kính R = 5 cm.
a) Tính độ dài cạnh của hình vuông nội tiếp trong (O).
b) Một hình chữ nhật nội tiếp (O) có chu vi 28 cm. Tính chiều dài và chiều rộng của hình chữ nhật đó.
Phương pháp giải - Xem chi tiết
Đọc kĩ dữ kiện để vẽ hình
Áp dụng định lý: Đường tròn ngoại tiếp hình vuông, hình chữ nhật có tâm là giao điểm của hai đường chéo và bán kính bằng nửa đường chéo. Sau đó áp dụng định lí pythagore để tính cạnh hình vuông, chiều dài, rộng hình chữ nhật.
Lời giải chi tiết
a)
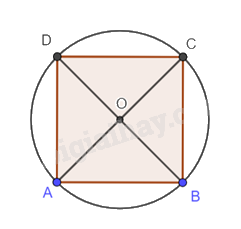
Ta có BD = 2OB = 2R = 2.5 = 10 cm.
Áp dụng định lý Pythagore trong tam giác vuông BAD ta có:
\(A{D^2} + A{B^2} = 2A{D^2} = BD\) suy ra AD = \(\sqrt {\frac{{BD}}{2}} = \sqrt {\frac{{10}}{2}} = \sqrt 5 cm\).
b)
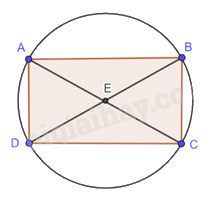
Ta có AC = 2AE = 2R = 2.5 = 10 cm.
Nửa chu vi hình chữ nhật là: 28 : 2 = 14 cm
Gọi AD = x suy ra CD = 14 – x
Áp dụng định lí Pythagore trong tam giác vuông ADC có:
\(\begin{array}{l}A{D^2} + C{D^2} = A{C^2}\\{x^2} + {\left( {14 - x} \right)^2} = {10^2}\\{x^2} + 196 - 28x + {x^2} - 100 = 0\\2{x^2} - 28x + 96 = 0\end{array}\)
Giải phương trình ta được AD = 6 cm và CD = 8 cm.
Bài tập 7.10 trang 38 SGK Toán 9 tập 2 yêu cầu chúng ta xét hàm số y = (m-2)x + 3. Để hàm số này là hàm số bậc nhất, điều kiện cần và đủ là hệ số của x khác 0, tức là m-2 ≠ 0. Việc hiểu rõ điều kiện này là nền tảng để giải quyết bài toán.
Đề bài yêu cầu tìm giá trị của m để hàm số y = (m-2)x + 3 là hàm số bậc nhất. Để làm được điều này, chúng ta cần nắm vững định nghĩa của hàm số bậc nhất và áp dụng điều kiện m-2 ≠ 0.
Để hàm số y = (m-2)x + 3 là hàm số bậc nhất, ta cần có:
m - 2 ≠ 0
Suy ra:
m ≠ 2
Vậy, với mọi giá trị của m khác 2, hàm số y = (m-2)x + 3 là hàm số bậc nhất.
Ví dụ 1: Nếu m = 3, hàm số trở thành y = (3-2)x + 3 = x + 3. Đây là hàm số bậc nhất vì hệ số của x là 1, khác 0.
Ví dụ 2: Nếu m = 2, hàm số trở thành y = (2-2)x + 3 = 3. Đây không phải là hàm số bậc nhất mà là hàm số hằng.
Hàm số bậc nhất có nhiều ứng dụng trong thực tế, ví dụ như:
Bài tập 7.10 trang 38 SGK Toán 9 tập 2 là một bài tập cơ bản về hàm số bậc nhất. Việc nắm vững kiến thức về hàm số bậc nhất và áp dụng điều kiện m ≠ 2 là chìa khóa để giải quyết bài toán này. Hãy luyện tập thêm các bài tập tương tự để củng cố kiến thức và kỹ năng của mình.
| Khái niệm | Định nghĩa |
|---|---|
| Hàm số bậc nhất | Hàm số có dạng y = ax + b, trong đó a và b là các số thực và a ≠ 0. |
| Hệ số góc | Số a trong hàm số y = ax + b. |
| Tung độ gốc | Số b trong hàm số y = ax + b. |
Hy vọng bài giải chi tiết này sẽ giúp các em hiểu rõ hơn về bài tập 7.10 trang 38 SGK Toán 9 tập 2 và tự tin hơn trong việc học toán.