Chào mừng các em học sinh đến với bài giải bài tập 7.18 trang 39 SGK Toán 9 tập 2 trên giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán. Đồng thời, chúng tôi cũng sẽ phân tích các bước giải, các lưu ý quan trọng để các em có thể tự giải các bài tập tương tự.
Bạn An sử dụng các hình viên phân như Hình 7.25a để ghép thành mẫu hoa văn trang trí như trong Hình 7.25b. Tính diện tích của mẫu hoa văn.
Đề bài
Bạn An sử dụng các hình viên phân như Hình 7.25a để ghép thành mẫu hoa văn trang trí như trong Hình 7.25b. Tính diện tích của mẫu hoa văn.
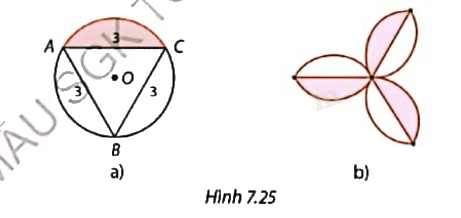
Phương pháp giải - Xem chi tiết
Tính bán kính đường tròn ngoại tiếp của tam giác đều bằng \(\frac{{a\sqrt 3 }}{3}\).
Tính diện tích đường tròn ngoại tiếp của tam giác đều là S = \(\frac{\pi {a^2}}{3}\)
Tính diện tích tam giác đều \(\frac{{{a^2}\sqrt 3 }}{4}\) với cạnh a rồi lấy diện tích đường tròn trừ đi diện tích tam giác ta tìm được diện tích một viên phân.
Lời giải chi tiết
Ta có bán kính đường tròn ngoại tiếp của tam giác đều bằng \(\sqrt 3 \).
Diện tích đường tròn ngoại tiếp của tam giác đều là:
S = \(\frac{\pi {3^2}}{3} = 3\pi \) cm2
Diện tích tam giác đều ABC là: \(\frac{{9\sqrt 3 }}{4}\) cm2
Diện tích 3 viên phân là:
\(3\pi - \frac{{9\sqrt 3 }}{4} \approx 5,5\) cm2
Mà mẫu hoa văn tạo thành từ 6 viên phân nên có diện tích là:
2.5,5 \( \approx \) 11 cm2.
Bài tập 7.18 trang 39 SGK Toán 9 tập 2 yêu cầu chúng ta giải một bài toán liên quan đến hàm số bậc nhất và ứng dụng. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về hàm số bậc nhất, bao gồm:
Trước khi bắt tay vào giải bài tập, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Điều này giúp chúng ta lựa chọn phương pháp giải phù hợp và tránh sai sót không đáng có.
Thông thường, đề bài sẽ yêu cầu chúng ta:
Để minh họa, chúng ta sẽ cùng nhau giải một ví dụ cụ thể. Giả sử đề bài yêu cầu chúng ta tìm hàm số bậc nhất y = ax + b biết rằng đồ thị của hàm số đi qua hai điểm A(1; 2) và B(-1; 0).
Thay A(1; 2) vào, ta được: 2 = a * 1 + b => a + b = 2 (1)
Thay B(-1; 0) vào, ta được: 0 = a * (-1) + b => -a + b = 0 (2)
Cộng (1) và (2), ta được: 2b = 2 => b = 1
Thay b = 1 vào (1), ta được: a + 1 = 2 => a = 1
Vậy hàm số bậc nhất cần tìm là y = x + 1.
Ngoài bài tập 7.18, còn rất nhiều bài tập tương tự liên quan đến hàm số bậc nhất. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải:
Phương pháp giải: Thay tọa độ của điểm thuộc đồ thị vào phương trình hàm số y = ax + b, sau đó giải phương trình để tìm b.
Phương pháp giải: Thay tọa độ của hai điểm thuộc đồ thị vào phương trình hàm số y = ax + b, sau đó giải hệ phương trình để tìm a và b.
Phương pháp giải: Đặt ẩn số, biểu diễn các đại lượng liên quan qua hàm số bậc nhất, sau đó giải phương trình hoặc hệ phương trình để tìm ẩn số.
Để giải bài tập về hàm số bậc nhất một cách chính xác và hiệu quả, các em cần lưu ý những điều sau:
Bài tập 7.18 trang 39 SGK Toán 9 tập 2 là một bài tập điển hình về hàm số bậc nhất. Hy vọng rằng với lời giải chi tiết và các hướng dẫn trên, các em đã nắm vững kiến thức và kỹ năng giải bài tập này. Chúc các em học tập tốt!